Terminale : La fonction logarithme népérien
Ce chapitre constitue la suite logique du chapitre sur l'exponentielle. Il est donc fortement conseillé au lecteur de lire ce chapitre avant de tenter d'appréhender cette nouvelle fonction.
📚 Table des matières
1. Définition
Définition 1.
Pour \(a \in \mathbb{R}\), l'équation \(e^x = a\) possède une unique solution strictement positive que l'on appelle logarithme népérien de \(a\), noté \(ln(a)\).
Remarque : L'unicité de la solution de l'équation \(e^x = a\) provient du corollaire du théorème des valeurs intermédiaire. En effet, \(exp\) est strictement croissante et continue sur \(\mathbb{R}\) à valeurs dans \(\mathbb{R_+^*}\). Donc, sa solution est unique et est un réel strictement positif.
Définition 2.
On appelle la fonction logarithme népérien, la fonction associant à \(x\) son logarithme népérien, et on la note \(ln\) :
D'après ce qui précède, cette fonction est bien définie sur \(\mathbb{R_+^*}\).
Exemple
Calculons quelques valeurs de logarithmes népériens :
Remarque : Par construction, les fonctions \(ln\) et \(exp\) sont réciproques donc on a les résultats suivants, qui seront primordiaux dans la suite du cours :
\[ \forall x \in \mathbb{R_+^*}, \quad \exp(ln(x)) = x \qquad \forall x \in \mathbb{R}, \quad ln(\exp(x)) = x\]
Graphiquement, on peut en déduire l'allure de la fonction \(ln\) construit par symétrie par rapport à la droite d'équation \(y=x\) de la courbe \(y=\exp(x)\) :
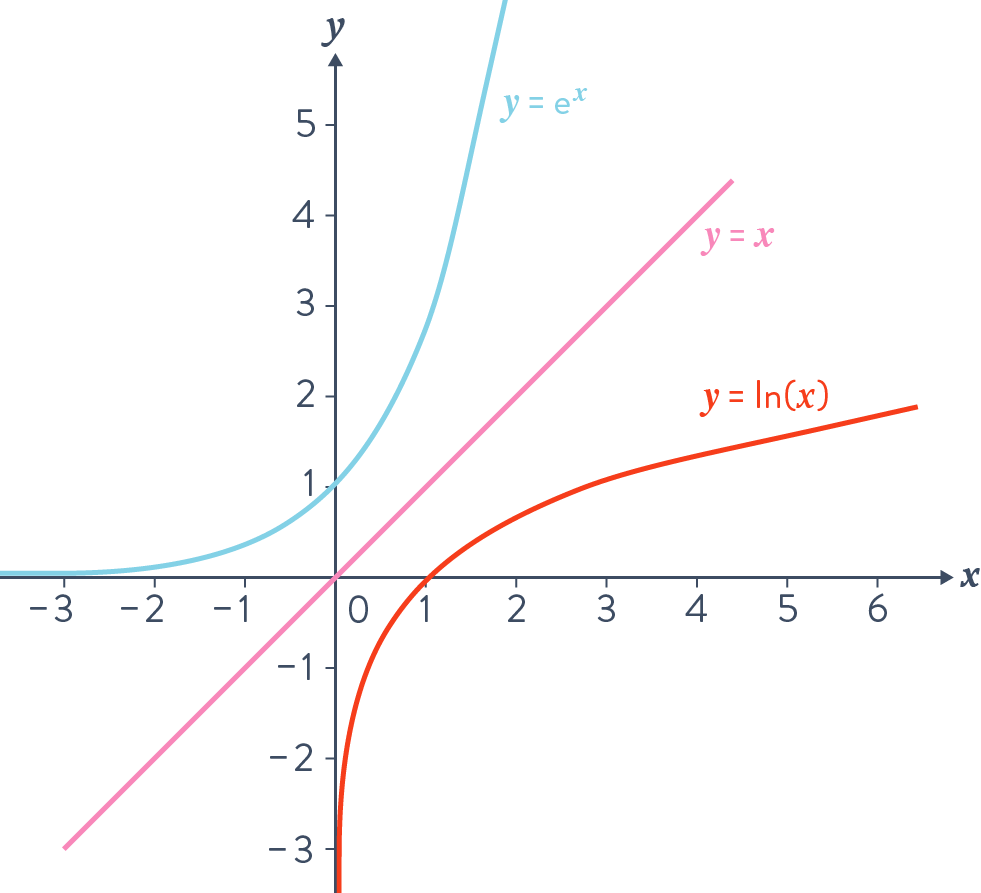
Figure 1. Représentation graphique de la réciprocité de \(ln\) et \(exp\).
2. Étude de la fonction \(ln\)
Proposition 1.
On obtient les conséquences suivantes :
1. \(ln(1)=0\)
2. \(\forall x,y \in \mathbb{R_+^*},\hspace{0.5cm} ln(x \times y) = ln(x) + ln(y)\)
3. \(\forall x,y \in \mathbb{R_+^*},\hspace{0.5cm} ln\left(\frac{x}{y}\right) = ln(x) - ln(y)\)
Preuve
Démontrons que \(\forall x,y \in \mathbb{R_+^*},\hspace{0.5cm} ln(x \times y) = ln(x) + ln(y)\) :
Soient \(x,y \in \mathbb{R_+^*}\), on observe que :
\[ e^{ln(x)+ln(y)} = e^{ln(x)} e^{ln(y)} = xy = e^{ln(xy)} \]
Puis, en utilisant le résultat de la définition 1, on en déduit le résultat.
On montre ensuite que : \(\forall x \in \mathbb{R_+^*},\hspace{0.5cm} ln\left(\frac{1}{x}\right) = -ln(x)\).
En effet, en adoptant le même raisonnement que précédemment :
\[ e^{-ln(x)} = \frac{1}{e^{ln(x)}} = \frac{1}{x} = e^{ln(\frac{1}{x})} \]
D'où le résultat.
Exemple de simplification
Simplifions l'expression \(A = ln(3) + ln(1/3)\) :
On sait que \(ln(1/3) = -ln(3)\), donc :
\[ A = ln(3) - ln(3) = 0 \]Ou encore en utilisant la propriété du produit :
\[ A = ln(3 \times \frac{1}{3}) = ln(1) = 0 \]3. Variations et limites
Proposition 2. (Dérivée de la fonction \(ln\))
La fonction \(ln\) est dérivable sur \(\mathbb{R_+^*}\) et sa dérivée a pour expression :
Preuve
La dérivabilité de la fonction \(ln\) est ici admise. On va simplement se contenter de démontrer l'expression de sa dérivée en revenant à la définition. En effet :
\[ \forall a \in \mathbb{R_+^*},\hspace{0.5cm} ln'(a) = \lim_{x \to a} \frac{ln(x)-ln(a)}{x-a} \]
Dès lors, il suffit de remarquer que : \( x = e^{ln(x)}\) et donc la relation suivante en découle, pour \(a \in \mathbb{R_+^*}\) :
\[ \begin{align*} ln'(a) &= \lim_{x \to a} \frac{ln(x)-ln(a)}{e^{ln(x)}-e^{ln(a)}}\\ &= \lim_{X \to ln(a)} \frac{X-ln(a)}{e^X-e^{ln(a)}}\\ &= \lim_{X \to ln(a)} \frac{1}{\frac{e^X-e^{ln(a)}}{X-ln(a)}} \end{align*} \]
On a ici effectué le changement de variable \(X=ln(x)\). Comme \(exp\) est dérivable, on en déduit donc :
\[ ln'(a) =\frac{1}{\exp'(ln(a))} = \frac{1}{a} \]
D'où le résultat.
Proposition 3.
La fonction \(ln\) est concave sur \(\mathbb{R_+^*}\).
Preuve
Il suffit de remarquer que :
\[ \forall x \in \mathbb{R_+^*},\hspace{0.5cm} ln''(x)=-\frac{1}{x^2} < 0 \]
Proposition 4.
La fonction \(ln\) possède des limites infinies en \(0\) et en \(+\infty\) :
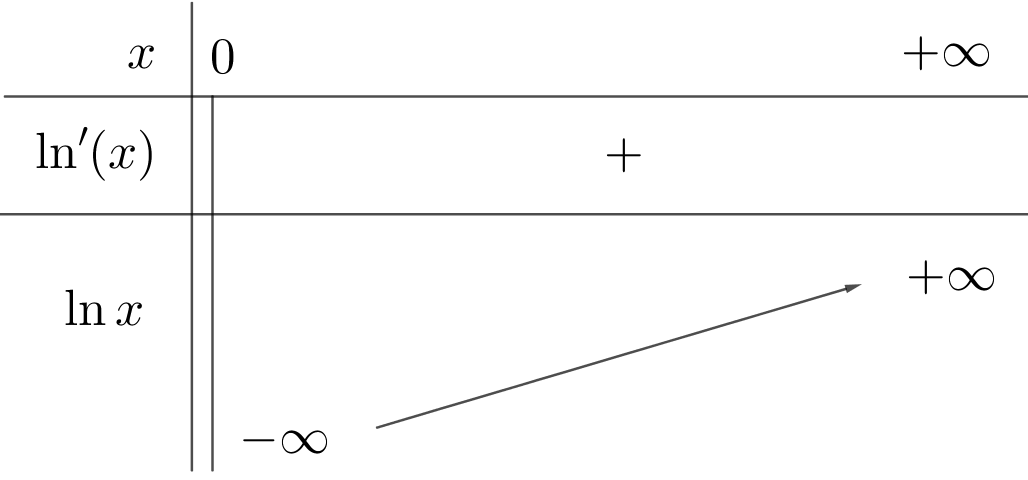
Figure 2. Tableau de variations de la fonction \(ln\).
4. Croissance comparée
Théorème 1.
Les fonctions \(ln\) et \(x \mapsto x^n \) pour \(n \in \mathbb{N}\) vérifient les résultats suivants :
Preuve
Le seul résultat au programme est l'étude de la limite de \(x \mapsto xln(x)\) en 0. Pour cela, on doit utiliser un prérequis (cf cours exponentielle) qui est le suivant :
\[ \lim_{{X \rightarrow -\infty}} X e^X = 0\]
Dès lors, on a (en posant \(X = ln(x)\)) :
\[ \begin{align*} \lim_{x \rightarrow 0^+} x ln(x) &= \lim_{x \rightarrow 0^+} e^{ln(x)} ln(x) \\ &= \lim_{X \rightarrow -\infty} e^X X \\ &= 0 \end{align*} \]
D'où le résultat.