Terminale : La fonction exponentielle
Dans ce chapitre, nous allons étudier une fonction fondamentale en analyse : la fonction exponentielle. Elle est indispensable pour modéliser de nombreux phénomènes physiques, biologiques et économiques (croissance de populations, désintégration radioactive, intérêts composés, etc.).
📚 Table des matières
1. Première approche
Théorème 1. (Théorème de l'exponentielle)
Il existe une unique fonction \(f : \mathbb{R} \to \mathbb{R}\) dérivable vérifiant :
\[ \forall x \in \mathbb{R} ,\hspace{0.5cm} f'(x) = f(x) \text{ avec } f(0)=1 \]Preuve
Dans ce type d'énoncé, il est primordial de démontrer l'unicité ET l'existence.
-
Unicité : Supposons qu'il existe une autre fonction \(g\) vérifiant les mêmes propriétés que \(f\). On souhaiterait montrer que \( g=f \). On introduit alors \(h_1:x \mapsto g(-x) f(x)\). Cette fonction est dérivable sur \(\mathbb{R}\) comme produit de fonctions dérivables et on a alors (formule de dérivée d'un produit) :
\begin{align*}
\forall x \in \mathbb{R},\hspace{0.5cm} h'(x) &= f'(x)g(-x) -f(x)g'(-x) \\
&= f(x)g(-x) - f(x)g(-x)\\
&=0
\end{align*}
Donc finalement, h est constante sur \(\mathbb{R}\) car de dérivée nulle et :
\[h(0) = f(0)g(0) = 1\]Donc, \(\forall x \in \mathbb{R}, g(-x)f(x) = 1 \). Or, en posant \(h_2:x \mapsto f(-x) f(x)\), on peut aussi montrer que \(h_2\) est constante égale à 1 (en calculant la dérivée et en évaluant en 0). Finalement :
\[ \forall x \in \mathbb{R}, \hspace{0.5cm} g(-x)f(x) = 1 = f(-x)f(x)\]Il ne reste plus qu'à simplifier par \(f(x)\), ce qui n'est possible que si f ne s'annule pas. Or, comme la fonction \(h_2\) ne s'annule pas, cela signifie directement que f n'est jamais nulle. En simplifiant :
\[ \forall x \in \mathbb{R}, \hspace{0.5cm} g(-x) = f(-x) \text{, autrement dit, } g=f\]D'où l'unicité.
- Existence (HORS-PROGRAMME EN TERMINALE) : Voir complément de cours.
Remarque : Il est toujours mieux de connaître la démonstration de l'exponentielle pour ceux souhaitant poursuivre dans les études scientifiques.
2. Définition et étude de l'exponentielle
Définition 1.
L'unique fonction vérifiant le théorème précédent est appellée fonction exponentielle et est notée exp.
Proposition 1.
On obtient les conséquences suivantes grâce à la définition précédente :
- \(exp(0)=1\)
- La fonction \(exp\) ne s'annule pas sur \(\mathbb{R}\)
- La fonction \(exp\) est continue et dérivable sur \(\mathbb{R}\)
- \(\forall x \in \mathbb{R},\hspace{0.5cm} exp'(x)=exp(x)\)
Preuve
Tous les résultats sont des conséquences immédiates de la définition 1 (et de la démonstration du théorème 1). Nous utilisons aussi le fait que dérivable \(\implies\) continue.
Exemple
Calculons l'image de quelques valeurs :
3. Variations et limites
Proposition 2.
La fonction \(exp\) est strictement croissante sur \(\mathbb{R}\).
Preuve
(HORS-PROGRAMME EN TERMINALE) Comme \(exp\) est dérivable sur \(\mathbb{R}\), nous pouvons nous intéresser dans un premier temps à ses variations. En effet, nous avons montré, dans la preuve du théorème 1, que la fonction exponentielle ne s'annule jamais et \(exp(0)=1 > 0 \). Alors, exp est strictement positive sur \(\mathbb{R}\) (continuité et théorème des valeurs intermédiaires). D'autre part :
\[ \forall x \in \mathbb{R},\hspace{0.5cm} exp'(x)=exp(x) > 0 \]D'où le résultat.
Proposition 3.
La fonction \(exp\) est convexe sur \(\mathbb{R}\).
Preuve
Il suffit de remarquer que :
\[ \forall x \in \mathbb{R},\hspace{0.5cm} exp''(x)=exp(x) > 0 \]Proposition 4.
Comme \(exp\) est continue sur \(\mathbb{R}\), il s'agit de déterminer les limites aux infinis :
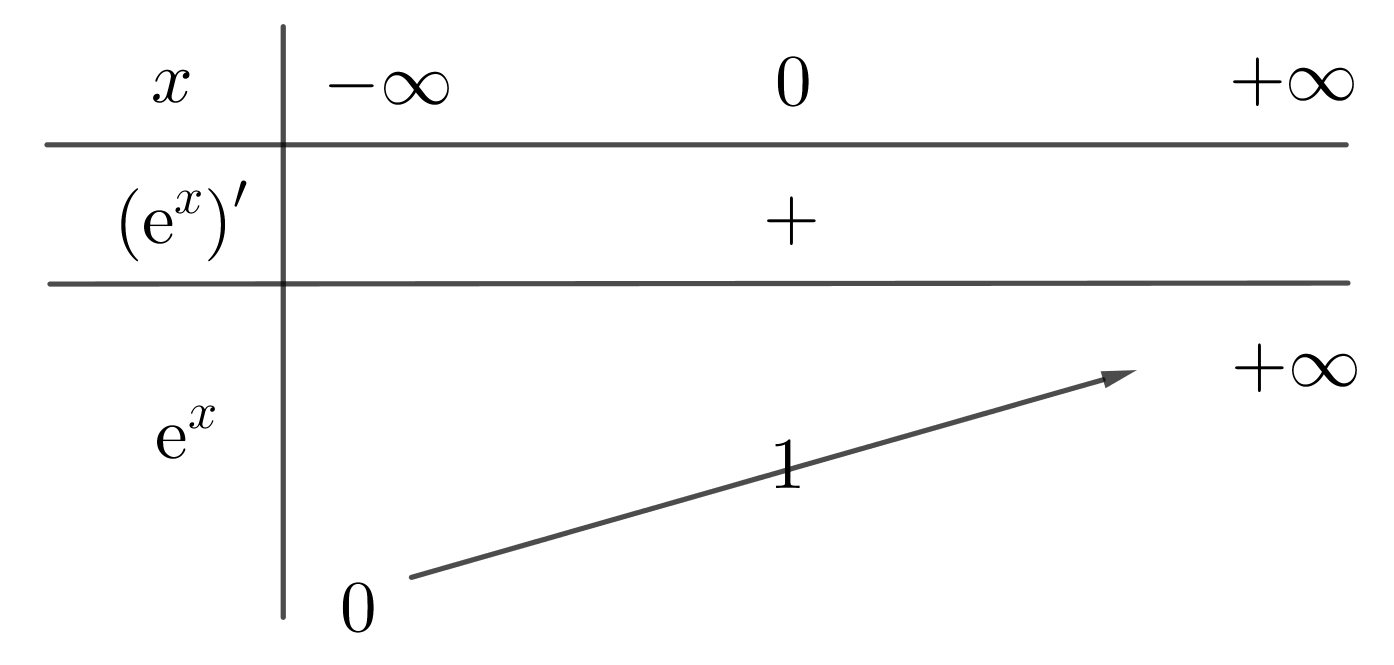
Figure 1. Tableau de variations de la fonction \(exp\).
4. Représentation graphique
En utilisant les résultats de la section précédente, nous pouvons en déduire une allure de la courbe représentant \(y=\exp(x)\). En effet :
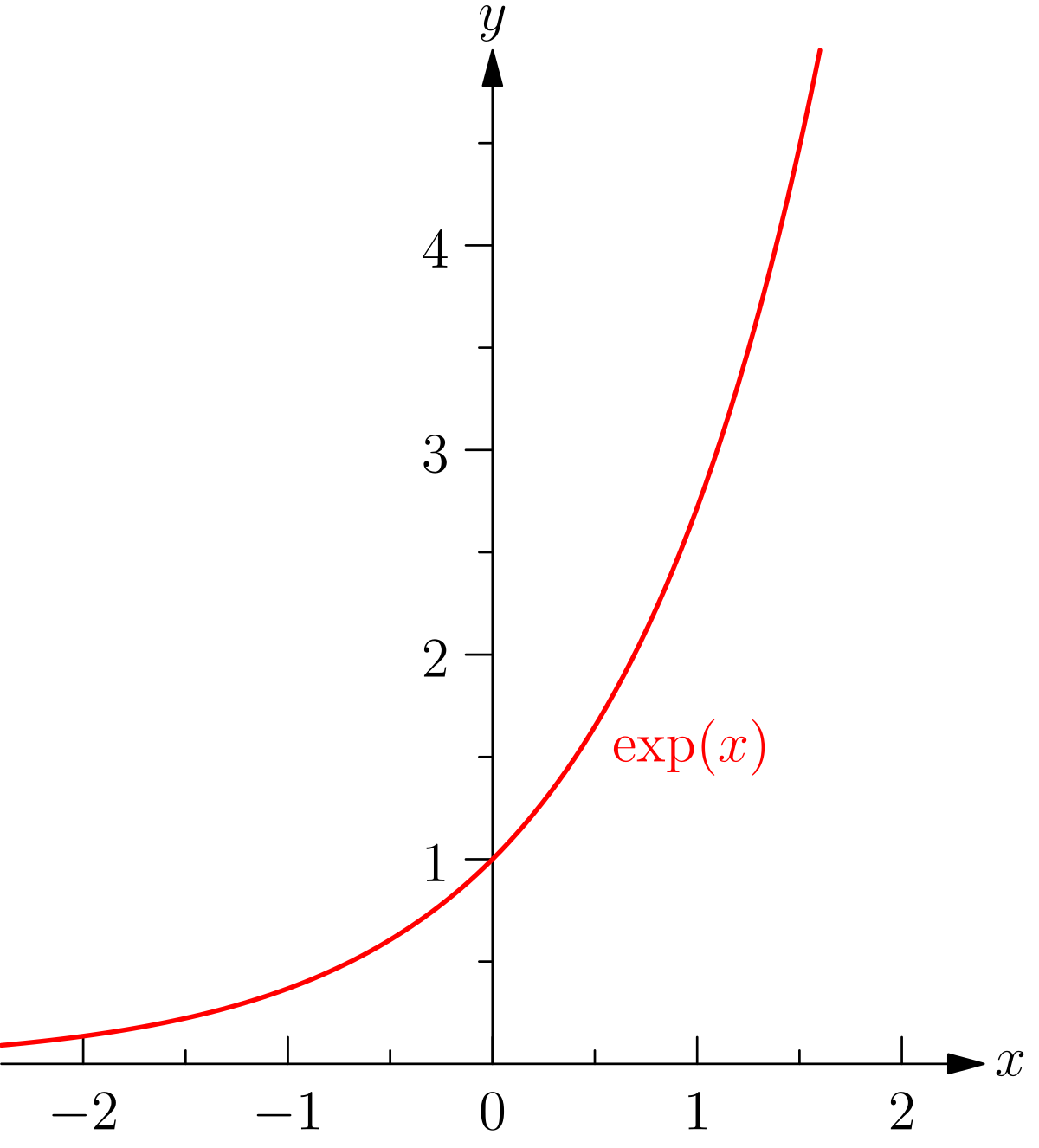
Figure 2. Représentation graphique de la fonction \(exp\).
5. Propriétés de l'exponentielle
Théorème 2.
La fonction \(exp\) vérifie les propriétés suivantes :
\[ \forall x,y \in \mathbb{R} ,\hspace{0.5cm} \exp(x+y)=\exp(x) \times \exp(y) \text{ et } \exp(x) \exp(-x) = 1 \]Preuve
Le deuxième résultat est immédiat en utilisant la démonstration du théorème 1, on a montré que \(h_2:x \mapsto \exp(-x) \exp(x) = 1\). Pour le premier résultat, on pose \(\phi : x \mapsto \frac{\exp(x+y)}{exp(x)exp(y)}\) avec \(y \in \mathbb{R}\) fixé. Cette fonction est dérivable en tant que quotient de fonctions dérivables dont le dénominateur ne s'annule pas et nous dérivons par rapport à x :
\[ \forall x \in \mathbb{R} ,\hspace{0.5cm} \phi'(x) = \frac{exp(x)exp(y)exp(x+y) - exp(y)exp(x)exp(x+y)}{(exp(x)exp(y))^2} = 0 \]Donc, la fonction est constante et : \(\phi(0) = 1\). Ceci étant vrai pour \(y \in \mathbb{R}\) quelconque, on en déduit le résultat.
Remarque : Comme on a montré que \(exp\) ne s'annule pas sur \(\mathbb{R}\), on peut alors écrire : \(\forall x \in \mathbb{R}, \exp(-x) = \frac{1}{\exp(x)}\)
Corollaire 1.
On en déduit les conséquences suivantes :
\( \forall x,y \in \mathbb{R} ,\hspace{0.5cm} \exp(x-y)=\frac{\exp(x)}{\exp(y)}\)
\( \forall x \in \mathbb{R} , \forall p \in \mathbb{N}, \hspace{0.5cm} \exp(px)= \exp(x)^p\)
Exemple de simplification
Simplifions l'expression \(A = \exp(3) \times \exp(-3)\) :
\[ A = \exp(3-3) = \exp(0) = 1 \]Notation : On note \(e\) l'image de 1 par la fonction \(exp\) :
\[ e = \exp(1) \]On élargit cette notation à \(x \in \mathbb{R}\) : \( e^x = \exp(x) \)
Remarque : On en déduit donc, en utilisant la nouvelle notation :
\[\forall x,y \in \mathbb{R},\hspace{0.5cm} e^{-x} = \frac{1}{e^{x}} \hspace{1cm} e^{x+y} = e^{x}e^{y} \hspace{1cm} e^{x-y} = \frac{e^{x}}{e^{y}}\]Proposition 5.
Pour tout nombre réels a et b :
\[ e^{a}=e^{b} \Leftrightarrow a=b \hspace{2cm} e^{a}<e^{b} \Leftrightarrow a < b \]6. Représentation des fonctions \(x \mapsto e^{kx}\) et \(x \mapsto e^{-kx}\)
Pour k un réel strictement positif, la fonction \(x \mapsto e^{kx}\) est strictement croissante et la fonction \(x \mapsto e^{-kx}\) est strictement décroissante et :
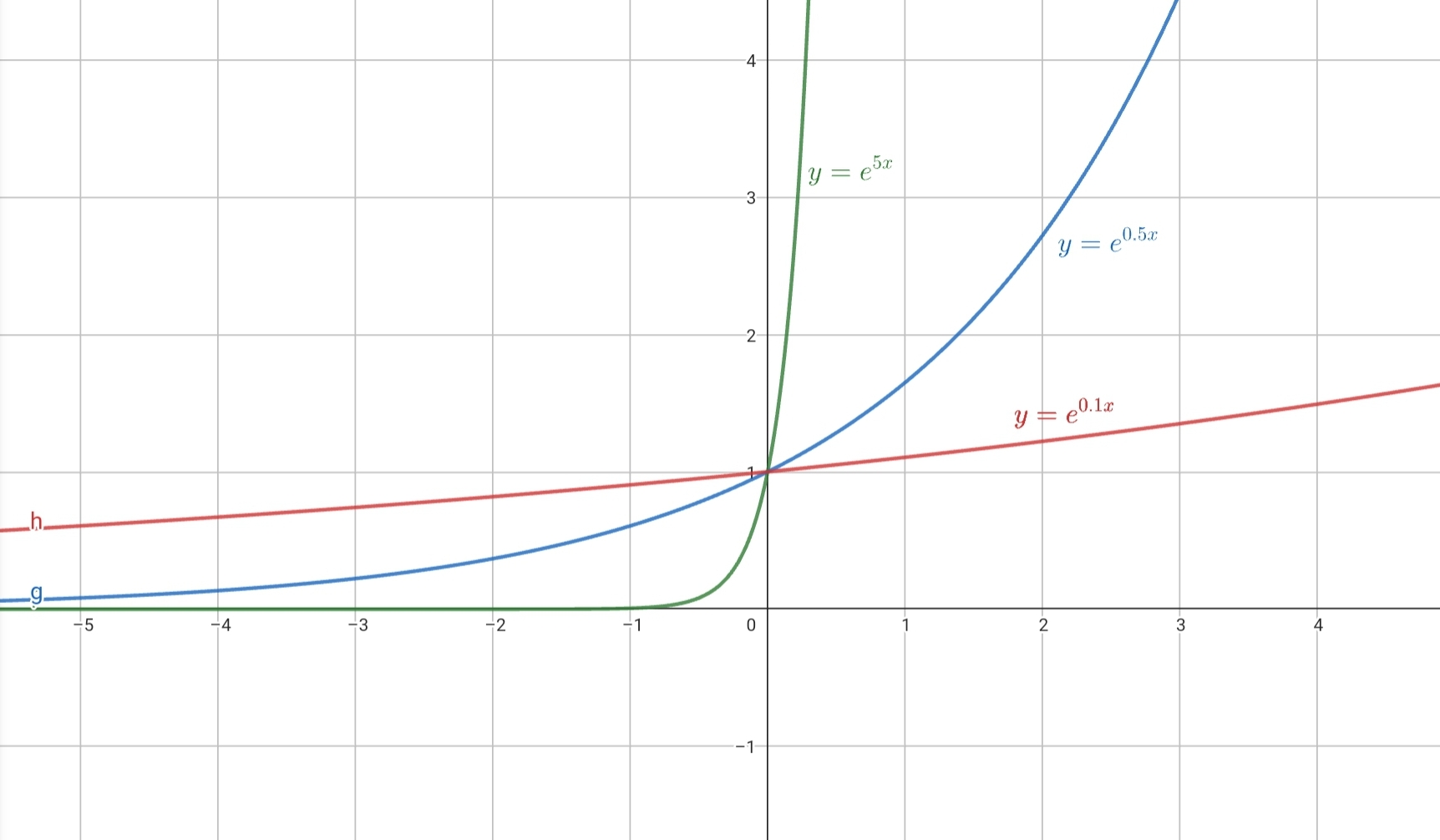
\(x \mapsto e^{kx}\)
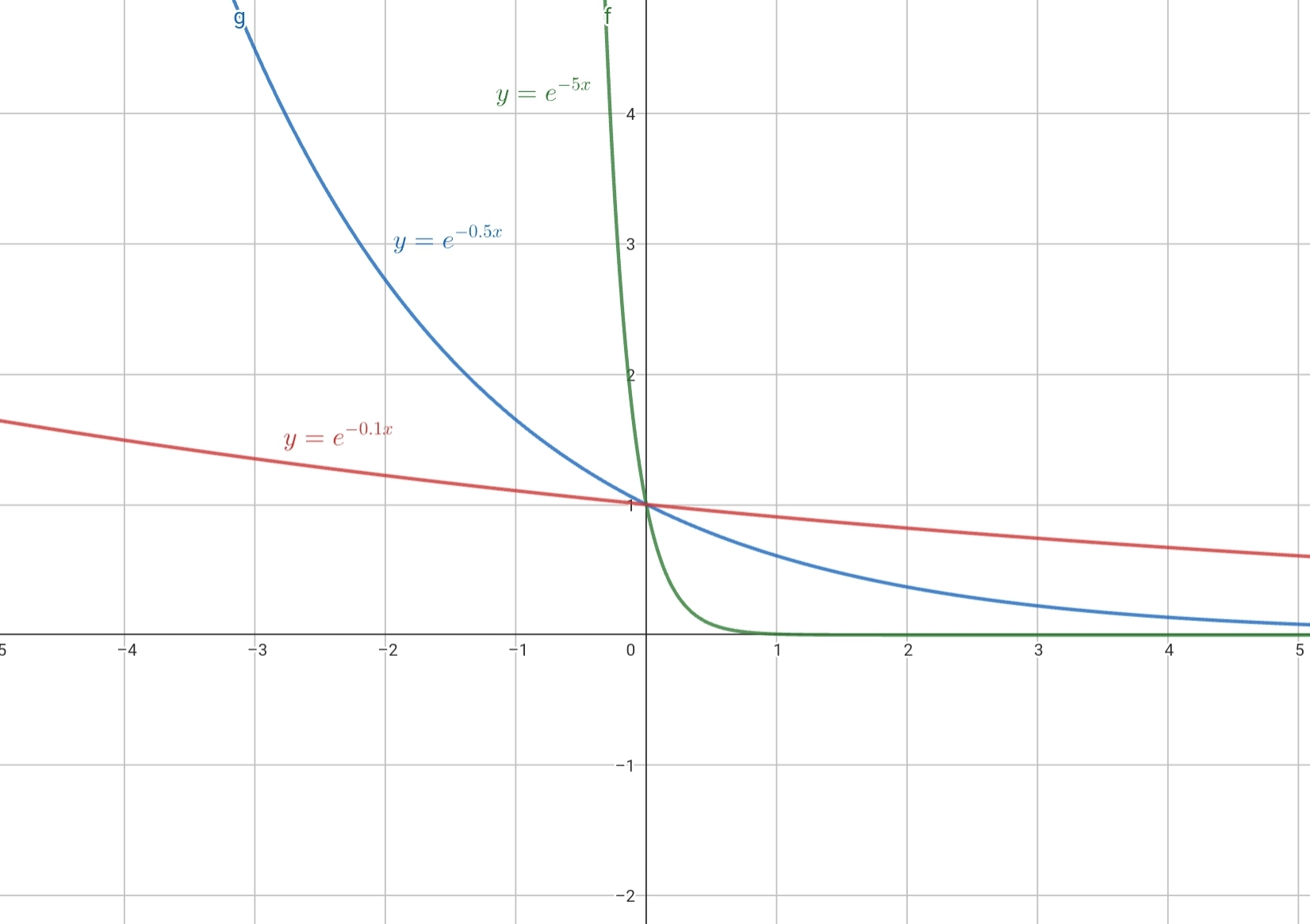
\(x \mapsto e^{-kx}\)
7. Etude de la suite géométrique (\(e^{nx}\))
Théorème 3.
La suite \((e^{nx})_{n \in \mathbb{N}}\) est géométrique de raison \(e^{x}\) et de premier terme \(e^{0}\).
Remarque : Ce résultat fait appel aux propriétés des suites géométriques.