Terminale : Suites numériques
📚 Table des matières
1. Le raisonnement par récurrence
1.1. Le principe
Le raisonnement par récurrence est une méthode classique en mathématiques pour démontrer un résultat.
Le principe est peut être expliqué de la manière suivante : Considérons une file de dominos. Dans cette file, si un domino tombe, le suivant aussi. Et ainsi de suite. Par conséquent, si l'on s'assure que le premier domino tombe, tous les dominos tomberont.
Définition 1 (Principe d'hérédité).
On dit qu’une propriété est héréditaire à partir d’un certain rang, si la propriété est vraie pour un entier naturel \(n\), alors elle est vraie pour l’entier suivant \(n+1\).
D'après le paragraphe sur les dominos, on peut en déduire une formalisation du principe de récurrence :
Définition 2 (Principe de récurrence).
Si la propriété \(P\) est :
1. vraie au premier rang \(k\) (Le k-ième domino tombe)
2. héréditaire à partir du premier rang \(k\) (Chaque domino placé après k-ième fait tomber le suivant),
Alors la propriété \(P\) est vraie pour tout entier \(n\) tel que : \(n \geq k\).
Exemple 1.
On considère la suite \((u_n)\) définie par \(u_0 = 1\) et, pour tout entier naturel \(n\),
Montrons que pour tout entier naturel \(n\), \(u_n > 0\).
Pour tout entier naturel \(n\), on pose \(P(n)\) : \(u_n > 0\).
Initialisation
Indication : On montre que la propriété est vraie au premier rang, ici n=0.
Pour \(n = 0\), on a \(u_0 = 1\) et donc \(u_0 > 0\). \(P(0)\) est vraie.
Hérédité
Indication : On fixe le rang n et on montre que la propriété est vraie au rang n+1.
Soit \(n \in \mathbb{N}\). Supposons que \(P(n)\) est vraie, c’est-à-dire \(u_n > 0\). Or, \(u_{n+1} = \frac{u_n}{1+u_n}\). \(u_{n+1}\) est donc le quotient de deux réels strictement positifs, il est donc strictement positif lui aussi. \(P(n+1)\) est vraie.
Conclusion
\(P(0)\) est vraie et \(P\) est héréditaire. Par récurrence, \(P(n)\) est vraie pour tout entier naturel \(n\).
1.2. Une inégalité intéressante
Proposition 1. (Inégalité de Bernoulli)
Soit un nombre réel \(x\) positif.
Pour tout entier naturel \(n\), on a : \((1 + x)^n \geq 1 + n \times x\)
La démonstration est présente dans le TD associé à ce chapitre.
2. Généralités
L'objectif de ce chapitre est d'étudier une catégorie particulière de fonctions définies sur \(\mathbb{N}\)
Définition 3 (Suites numériques).
On appelle suite numérique, une fonction \(u\) définie sur \(\mathbb{N}\) (= l'ensemble des entiers naturels). On note par convention : \(u(n) = u_n\).
La suite u est en général notée \((u_n)_{n \in \mathbb{N}}\).
L'objectif de ce chapitre sera de traduire des situations concrètes sous forme de suites.
Comme pour une fonction, on peut représenter graphiquement les termes d'une suite :
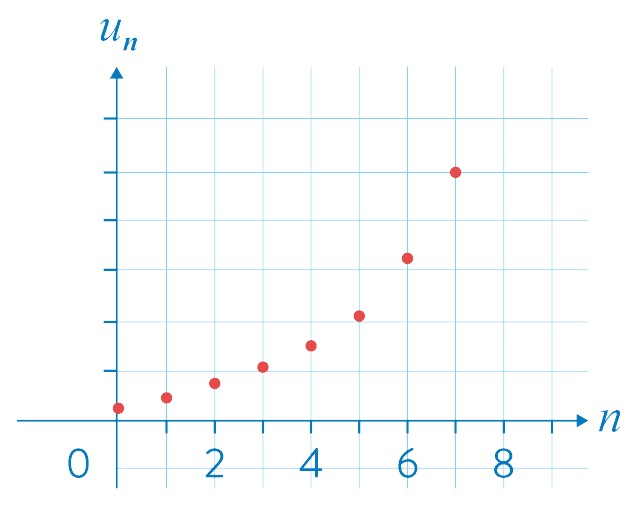
Figure 1. Représentation des termes d'une suite en fonction de \(n\)
2.1. Suite définie explicitement
Proposition 2.
Une suite \((u_n)_{n \in \mathbb{N}}\) est dite définie de manière explicite s'il existe une relation entre le terme \(u_n\) et \(n\), autrement dit, il existe une fonction \(f\) tel que :
2.2. Suite définie par une relation de récurrence
Proposition 3.
Une suite \((u_n)_{n \in \mathbb{N}}\) est dite définie par une relation de récurrence lorsque cette suite est complètement définie par :
1. Son premier terme (en règle générale \(u_0\))
2. Une relation (dite de récurrence) entre \(u_n\) et \(u_{n+1}\) pour \(n \in \mathbb{N}\).
3. Étude de la monotonie
Comme pour une fonction, on s'intéresse désormais au sens de variation d'une suite.
Proposition 4.
Les caractérisations suivantes permettent d'étudier la monotonie d'une suite :
1. Si pour tout \(n \in \mathbb{N}\), \(u_n \leq u_{n+1}\) alors \((u_n)_{n \in \mathbb{N}}\) est croissante.
2. De manière analogue, si pour tout \(n \in \mathbb{N}\), \(u_n \geq u_{n+1}\) alors \((u_n)_{n \in \mathbb{N}}\) est décroissante.
Exemple 2.
Point méthode : On peut chercher à comparer \(u_{n+1} – u_n\) à 0, ou si tous les termes de la suite sont strictement positifs, on peut comparer \(\frac{u_{n+1}}{u_n}\) à 1.
Considérons la suite \((u_n)\) définie pour tout entier naturel \(n\) par : \(u_n = 2n + 3\). Ici :
On en déduit que la suite est croissante.
4. Suites majorées, bornées et minorées
Définition 4.
1. La suite \((u_n)\) est majorée s'il existe un réel \(M\) tel que pour tout entier naturel \(n\), on a : \[ u_n \leq M. \]
2. La suite \((u_n)\) est minorée s'il existe un réel \(m\) tel que pour tout entier naturel \(n\), on a : \[ u_n \geq m. \]
3. La suite \((u_n)\) est bornée si elle est à la fois majorée et minorée.
5. Limite d'une suite
On note \(\lim_{n \to +\infty} u_n\) la limite d'une suite lorsqu'elle existe.
Remarque : Seule la limite en \(+ \infty\) est considérée.
Définition 5.
On dit qu'une suite est convergente si \(\lim_{n \to +\infty} u_n = a\) avec a un réel.
Une suite ne converge pas forcément.
Définition 6.
On dit qu'une suite \((U_n)\) admet pour limite \(\pm \infty\), si \(U_n\) est aussi grand que l’on veut à partir d'un certain rang et on note : \(\lim_{n \to +\infty} u_n = \pm \infty\)
Plus généralement, lorsqu'une suite n'est pas convergente, on dira qu'elle est divergente.
Exemple 3.
Soit la suite \((u_n)\) définie pour tout \(n \in \mathbb{N}\) : \(u_n = 2n+1\). On remarque que plus \(n\) augmente, plus \(u_n\) augmente aussi sans être majoré. On en déduit :
5.1. Théorèmes de comparaison
Soient \(l\) un nombre réel et \((u_n)\), \((v_n)\) et \((w_n)\) trois suites.
Théorème 1. (Théorème des "Gendarmes")
Si à partir d'un certain rang \(n\), on a :
1. \(v_n \leq u_n \leq w_n\)
2. \(\displaystyle\lim_{n \to +\infty} v_n = \displaystyle\lim_{n \to +\infty} w_n = l\)
Alors : \(\displaystyle\lim_{n \to +\infty} u_n = l\)
Théorème 2. (Théorème de comparaison)
Si à partir d'un certain rang \(n\), on a :
1. \(u_n \geq v_n\)
2. \(\displaystyle\lim_{n \to +\infty} v_n = +\infty\)
Alors : \(\displaystyle\lim_{n \to +\infty} u_n = +\infty\)
Théorème 2. (Théorème de comparaison version \(-\infty\))
Si à partir d'un certain rang \(n\), on a :
1. \(u_n \leq v_n\)
2. \(\displaystyle\lim_{n \to +\infty} v_n = -\infty\)
Alors : \(\displaystyle\lim_{n \to +\infty} u_n = -\infty\)
Pour étudier plus facilement une suite, nous allons dans la suite du chapitre considéré différents types de suites et énoncer de nombreux résultats, facilitant de ce fait l'étude d'une suite.
6. Suite arithmétique
Définition 7 (Suites arithmétiques).
On appelle suite arithmétique, toute suite \((u_n)_{n \in \mathbb{N}}\) définie par une relation récurrente de la forme :
où r est un réel appelé raison de la suite \((u_n)\).
En réitérant la relation de récurrence, on remarque que : \( u_{n} = u_{n-1} + r = u_{n-2} + 2r = ... = u_0 + nr \). On en déduit :
Proposition 5.
Soit \((u_n)_{n \in \mathbb{N}}\) une suite arithmétique de raison \(r \in \mathbb{R}\), alors pour \(n \in \mathbb{N}\):
L'étude de la monotonie d'une telle suite est directe, en remarquant : \( u_{n+1} - u_n = r \). Donc, \((u_n)_{n \in \mathbb{N}}\) est croissante (respectivement décroissante) seulement si \(r \geq 0\) (respectivement si \(r \leq 0\)).
Il existe des cas concrets de suites arithmétiques. Par exemple, si un patient reçoit 15 médicaments par semaine, alors le nombre de médicaments reçus par le patient définit une suite arithmétique de la forme : \(u_{n+1} = u_n + 15\).
7. Suite géométrique
Définition 8 (Suites géométriques).
On appelle suite géométrique, toute suite \((u_n)_{n \in \mathbb{N}}\) définie par une relation récurrente de la forme :
où q est un réel appelé raison de la suite \((u_n)\).
En réitérant la relation de récurrence, comme dans le cas des suites arithmétiques, on trouve :
Proposition 6.
Soit \((u_n)_{n \in \mathbb{N}}\) une suite géométrique de raison \(q \in \mathbb{R}\), alors pour \(n \in \mathbb{N}\):
L'étude de la monotonie d'une telle suite est directe, en remarquant (si \(u_n \neq 0\)): \( \frac{u_{n+1}}{u_n} = q \). Donc, \((u_n)_{n \in \mathbb{N}}\) est croissante (respectivement décroissante) seulement si \(q \geq 1\) (respectivement si \(q \leq 1\)).
8. Somme de suites arithmétiques
Proposition 7 (Somme d'une suite arithmétique).
Soit \((u_n)\) une suite arithmétique de raison \(r\) et de premier terme \(u_0\). La somme des \(n+1\) premiers termes est donnée par :
Exemple 4.
Calculons la somme des 10 premiers termes d'une suite arithmétique de raison \(r=2\) et de premier terme \(u_0 = 1\).
D'abord, \(u_{10} = u_0 + 10r = 1 + 10(2) = 21\). (Attention, $S_{10}$ est la somme de 11 termes, de k=0 à k=10).
Calculons \(S_{10} = \sum_{k=0}^{10} u_k\). Il y a \(n+1 = 10+1 = 11\) termes.
9. Somme de suites géométriques
Proposition 8 (Somme d'une suite géométrique).
Soit \((u_n)\) une suite géométrique de raison \(q \neq 1\) et de premier terme \(u_0\). La somme des \(n+1\) premiers termes est donnée par :
Exemple 5.
Calculons la somme des 5 premiers termes d'une suite géométrique de raison \(q=2\) et de premier terme \(u_0 = 1\).
Calcul de \(S_4\) (les 5 premiers termes, de k=0 à k=4) :
Calcul de \(S_5\) (les 6 premiers termes, de k=0 à k=5) :