Terminale : Mathématiques : Continuité
Dans tout ce chapitre, on définit \(I\) comme un intervalle ouvert de \(\mathbb{R}\).
📚 Table des matières
1. Définitions
Soient \(a \in I\) et \(f : I \mapsto \mathbb{R}\) :
Définition 1. (Continuité en un point et généralisation)
Soit \(f\) une fonction définie sur \(I\) et \(a\) un nombre réel contenu dans cet intervalle. On dit que \(f\) est continue en \(a\) si :
Alors, la fonction \(f\) est définie sur tout l'intervalle \(I\) si et seulement si elle est continue en chacun des points de cet intervalle.
Interprétation graphique.
Une fonction \(f\) est continue sur un intervalle si l'on peut tracer sa représentation graphique sans avoir besoin de "lever" son stylo.
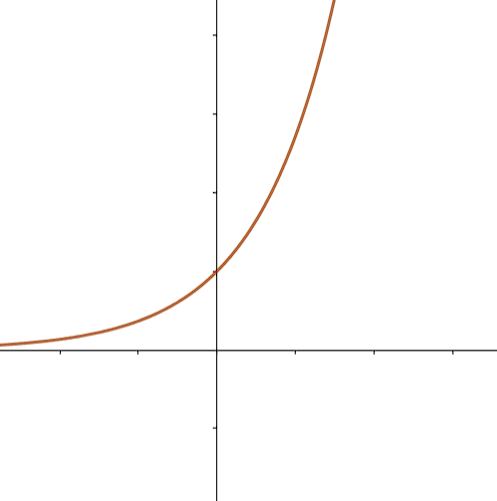
Figure 1. La fonction \(f\) est continue
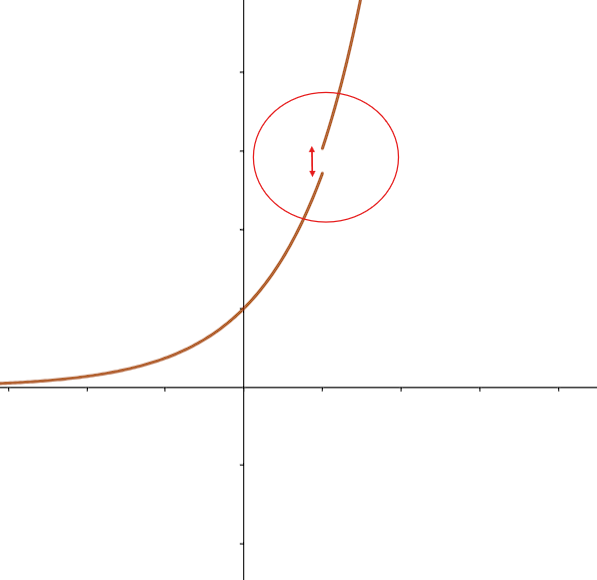
Figure 2. La fonction \(f\) n'est PAS continue
En règle générale, à chaque fois qu'une fonction possède une discontinuité, on observe un saut au point de discontinuité, comme c'est le cas de la fonction de droite (pour les plus curieux, il s'agit de la fonction partie entière).
Néanmoins, cela n'est pas toujours vrai, en considérant par exemple la fonction \(g\) suivante :
On obtient la représentation suivante :
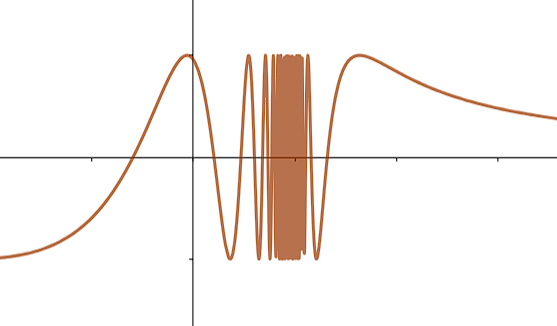
Figure 3. Représentation graphique de la fonction \(g\)
Cela reste néanmoins des cas moins fréquents.
2. Fonctions usuelles
De manière analogue à l'opérateur dérivée, on liste ici le domaine de continuité des fonctions usuelles, celles que l'on traite de manière générale au lycée.
Propriété 1 (Tableau récapitulatif).
| Fonction usuelle | Domaine de continuité |
|---|---|
| \(f(x) = x^n, \, n \in \mathbb{N}\) | \(\mathbb{R}\) |
| \(f(x) = \frac{1}{x^n}, \, n \in \mathbb{N}^*\) | \(]-\infty, 0[ \cup ]0, +\infty[\) |
| \(f(x) = \sqrt{x}\) | \([0, +\infty[\) |
| \(f(x) = e^x\) | \(\mathbb{R}\) |
| \(f(x) = \sin x \, \text{;} \, f(x) = \cos x\) | \(\mathbb{R}\) |
3. Opérations sur les fonctions continues
Propriété 2.
Toutes fonctions obtenues par somme, produit, quotient ou composition de fonctions de référence sont continues sur leur ensemble de définition.
Cette propriété permet de déterminer rapidement en général si une fonction est continue ou non :
Exemple 1.
Prenons comme exemple la fonction \(f : x \mapsto e^{x+2}\). On sait (d'après le tableau précédent) que les fonctions \(g : y \mapsto e^y\) et \(h : x \mapsto x+2\) sont continues sur \(\mathbb{R}\). Alors, par composition, on en déduit que \(f = g \circ h\) est continue sur \(\mathbb{R}\).
4. Théorèmes importants
Théorème 1.(Théorème des valeurs intermédiaires)
Pour toute fonction continue \( f : [a, b] \to \mathbb{R} \) et tout réel \( u \) compris entre \( f(a) \) et \( f(b) \), il existe au moins un réel \( c \) compris entre \( a \) et \( b \) tel que \( f(c) = u \).
Ce théorème permet d'affirmer que pour une fonction \(f\) continue sur un intervalle \([a,b]\), \(f(x)\) prend nécessairement toutes les valeurs entre \(f(a)\) et \(f(b)\). Graphiquement :
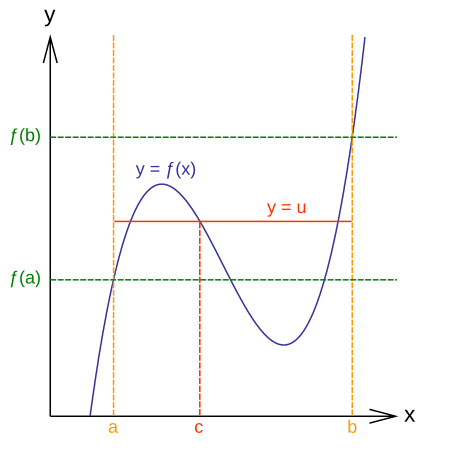
Figure 4. Interprétation graphique
On observe sur la figure 4 que la solution \(y=u\) n'est pas unique. Pour s'assurer de l'unicité de la solution, il faut ajouter des hypothèses:
Théorème 2.(Corollaire strictement monotone du TVI)
Pour toute fonction continue ET strictement monotone \( f : [a, b] \to \mathbb{R} \) et tout réel \( u \) compris entre \( f(a) \) et \( f(b) \), il existe un UNIQUE réel \( c \) compris entre \( a \) et \( b \) tel que \( f(c) = u \).
Exemple 2.
Dans cet exemple, démontrons que l'équation \(\cos(x) = x\) admet une solution unique dans l'intervalle \(]0 ; \pi[\).
Ici, nous allons utiliser le théorème précédent, en posant \(f(x) = \cos(x) - x\). On montre que l'équation \(f(x) = 0\) possède une unique solution. Étudions les variations de la fonction \(f\).
Comme \(f'(x) = -\sin(x) - 1 < 0\) sur \([0 ; \pi]\), \(f\) est strictement décroissante sur \([0 ; \pi]\). De plus, \(f(0) = \cos(0) - 0 = 1 > 0\) et \(f(\pi) = \cos(\pi) - \pi = -1 - \pi < 0\), donc \(f(\pi) < 0 < f(0)\).
De ce fait, l'équation \(f(x) = 0\) admet une unique solution dans l'intervalle \(]0 ; \pi[\). D'où \(\cos(x) = x\) aussi.
L'interprétation graphique peut permettre de mieux comprendre l'exemple. Voici le graphe de la fonction \(f\) définie dans l'exemple :
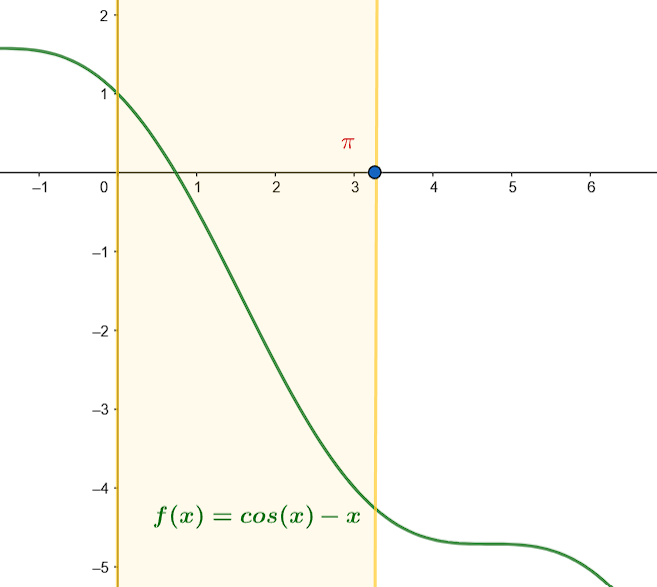
Figure 5. Représentation graphique de \(f\)
Graphiquement, on observe bien que \(f\) ne coupe l'axe des abscisses qu'une unique fois.
Enfin, un dernier théorème intéressant à étudier concerne l'image d'une suite convergente par une fonction continue :
Théorème 3.
Soit \((u_n)\) une suite à valeurs dans un intervalle \([a,b]\) et \(f\) une fonction définie et continue sur \([a,b]\). Si \((u_n)\) converge vers \(l \in [a,b]\), alors la suite de terme général \(f(u_n)\) converge vers \(f(l)\).
Exemple 3.
Rappel : théorème du point fixe
Considérons une suite \((u_n)\) une suite définie par récurrence de la manière suivante :
où \(f\) est une fonction continue sur \(\mathbb{R}\). Si \((u_n)\) converge vers \(l\), alors \(l\) est un point fixe de \(f\) et vérifie \(f(l) = l\).
Application
Soit \(u_0 = 1\) et \(\forall n \in \mathbb{N}, \quad u_{n+1} = \frac{1}{2}\left(u_n + \frac{a}{u_n}\right)\) avec \(a > 0\) et \(a \neq 1\). Il s'agit de montrer que \((u_n)\) converge vers \(\sqrt{a}\).
Raisonnons par récurrence sur \(n \in \mathbb{N}^*\) en montrant que \(u_n > \sqrt{a}\) :
Initialisation :
Pour \(n = 1\), il s'agit de montrer que \(u_1 > \sqrt{a}\)
Mais
donc, en manipulant l'inégalité, on obtient :
Hérédité :
Soit \(n \in \mathbb{N}^*\). On suppose \(u_n > \sqrt{a}\) (hypothèse de récurrence), alors :
Enfin, calculons \(u_{n+1} - u_n\) :
donc \((u_n)\) est décroissante et minorée par \(\sqrt{a}\).
Elle converge donc vers un réel positif qui vérifie le théorème du point fixe : \(l = f(l)\). Autrement dit :
Les solutions de cette équation sont
On ne retient que la valeur positive. D'où le résultat.
5. Lien entre dérivation et continuité
Propriété 3.
Si \(f\) est une fonction dérivable sur I, alors \(f\) est continue sur cet intervalle.