Terminale : Mouvement des corps célestes
Dans le cours sur l'étude d'un mouvement dans un champ uniforme nous avons été amenés à étudier le cas du mouvement d'un projectile dans un champ gravitationnel uniforme. La méthode de résolution est exactement la même, nous ne parlerons plus de \(g\) comme étant l'intensité de pesanteur terrestre mais nous parlerons de la norme du vecteur gravitationnel qu'on notera \(\mathcal{G}\) pour retrouver des résultats équivalents dans la section 1.
L'objectif de ce cours est étudier plus précisément comment se comporte les corps célestes dans un champ gravitationnel uniforme, en général, celui généré par leur corps attracteur (on définira ce terme plus loin). Ce cours offre ainsi une bonne ouverture sur les résultats fondamentaux en astronomie et propose, pour les plus tenaces, un point d'étude mathématique des outils manipulés en section 3.
📚 Table des matières
1. Étude du mouvement d'un corps céleste dans un champ gravitationnel uniforme
Dans cette première section, nous allons manier des outils déjà définis dans le cours sur la cinématique du point matériel pour les appliquer grâce aux notions développées dans le cours sur la dynamique du point matériel. Nous nous plaçons dans la situation suivante : on considère deux objets célestes (planètes, étoiles, galaxies, trous noirs, nébuleuses...). On suppose qu'ils sont distants d'une distance qui peut varier au cours du temps notée \(r(t)\) à l'instant \(t\).
Nous ferons l'hypothèse que l'on peut assimiler les deux objets à des points matériels qu'on pourra repérer par les points \(O\) et \(A\), c'est l'hypothèse du point matériel (cf. cours sur la cinématique du point matériel). On fixe un référentiel dont l'origine du repère spatial associé sera le point \(O\). On supposera que ce référentiel est galiléen.
Nous pouvons représenter la situation étudiée par la figure suivante :
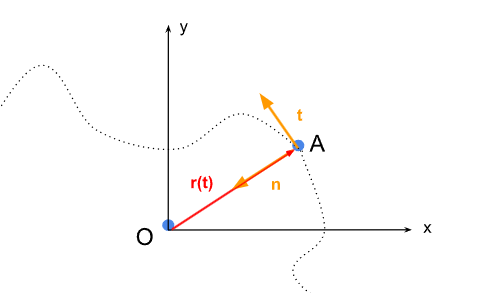
Figure 1. - Mise en situation du problème étudié
Remarque : Les hypothèses précédentes sont généralement toujours « admises » en exercice dans le cas où on étudie par exemple le mouvement de la Terre autour du Soleil ou encore celui de la Lune autour de la Terre.
Comme réalisé sur la figure 1, nous placerons en \(A\) un repère de Frenet car dans un mouvement curviligne, c'est le repère le plus adapté pour étudier le mouvement de \(A\) autour de \(O\). On notera par la suite \(M_O\) et \(M_A\) les masses respectives de \(O\) et \(A\).
1.1. Expression de l'accélération
On cherche à étudier le mouvement du système {objet A} dans le référentiel dont le repère spatial est lié à \(O\) supposé galiléen. La seule force qui s'exerce dans ce cas sur \(A\) est la force gravitationnelle appliqué par \(O\) en \(A\) notée \(\vec{F}_G\). En effet, on supposera que le système {objets O et A} est isolé. Le principe fondamental de la dynamique permet d'écrire : \[ M_A\vec{a}_A=\vec{F}_G \quad (1) \] avec \(\vec{a}_A\) est l'accélération de \(A\) dans le référentiel choisi.
Nous allons ajouter une hypothèse : comme \(O\) est fixe dans le temps alors l'écriture de l'accélération dans le repère de Frenet n'est pas donnée explicitement dans le cours car le rayon \(r\) varie au cours du temps pour un mouvement curviligne. Ainsi, nous supposerons que \(r\) est une constante. On notera par la suite \(v_A\) la vitesse de \(A\). On sait que : \[ \vec{a}_A=\frac{dv_A(t)}{dt}\vec{t}+\frac{v_A^2(t)}{r}\vec{n} \] et d'autre part, \[ \vec{F}_G=G\frac{M_OM_A}{r^2}\vec{n} \] où \(G\) est la constante de gravitation universelle.
En regroupant ces expressions dans (1), on a : \[ M_A\left(\frac{dv_A(t)}{dt}\vec{t}+\frac{v_A^2(t)}{r}\vec{n}\right)=G\frac{M_OM_A}{r^2}\vec{n} \] par identification, il en suit que la composante tangentielle de l'accélération notée \(\vec{a}_{A_T}\) est nulle au cours du temps donc la vitesse du mobile \(A\) est constante au cours du temps. D'autre part, la composante normale de l'accélération notée \(\vec{a}_{A_{N}}\) vérifie : \[ \vec{a}_{A_{N}}=\frac{v_A^2}{r}\vec{n}=G\frac{M_O}{r^2}\vec{n} \] on en déduit alors l'expression de l'accélération, en norme :
1.2. Expression la vitesse
Ici, il suffit de reprendre la partie 1.1 en réécrivant l'égalité suivante : \[ \frac{v_A^2}{r}\vec{n}=G\frac{M_O}{r^2}\vec{n} \] par projection suivant \(\vec{n}\), les termes constants sont alors égaux : \[ \frac{v_A^2}{r}=G\frac{M_O}{r^2} \] comme dit précédemment, dans le cas où \(r\) est une constante alors la vitesse est aussi une constante donc on pourra omettre la dépendance temporelle dans la vitesse \(v_A(t)\). On peut donc écrire :
2. Les lois de Kepler
2.1. Première loi de Kepler ou loi des orbites
Cette première loi permet de connaître la forme des orbites des planètes autour du Soleil.
Première loi. (La loi des orbites)
Toutes les planètes du système solaire décrivent des trajectoires elliptiques, dont le Soleil occupe l'un des foyers.
Pour comprendre ce premier énoncé, étudions l'une des huit planètes du système solaire qui sont dans l'ordre : Mercure, Vénus, la Terre, Mars, Jupiter, Saturne, Uranus et Neptune. Étudions par exemple Jupiter.
Jupiter gravite autour du Soleil et sa trajectoire autour du Soleil est une ellipse (cf. section 4 ou cours sur la cinématique du point matériel). Dans une ellipse, il existe deux points particuliers appelés foyers (cf. section 4) et l'un sera occupé par le Soleil. Voici un dessin de la situation suivante :
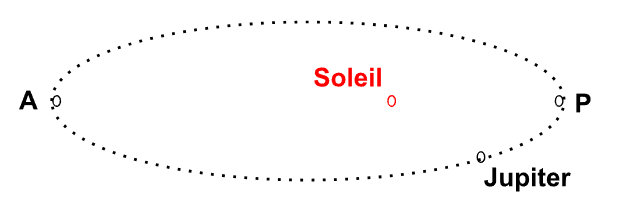
Figure 2. - Mouvement de Jupiter autour du Soleil
On notera tout de même que l'ellipse est « moins » prononcée que ça dans la réalité, elle est moins aplatie, autrement-dit elle se rapproche d'un cercle.
Définition 1. (Le périhélie)
Le périhélie est le point de la trajectoire elliptique d'un objet céleste autour du Soleil le plus proche de ce dernier.
Remarque : Sur la figure 2, cela correspond au point P.
Définition 2. (L'aphélie)
L'aphélie est le point de la trajectoire elliptique d'un objet céleste autour du Soleil le plus proche de ce dernier.
Remarque : Sur la figure 2, cela correspond au point A.
2.2. Seconde loi de Kepler ou loi des aires
Définition 3. (La rayon vecteur)
Le rayon vecteur est le vecteur qui a pour extrémités le Soleil et l'objet étudié sur son orbite elliptique.
Remarque : Le rayon vecteur est l'équivalent du diamètre lorsque l'ellipse est confondue à un cercle.
Définition 4. (Le corps attracteur)
Le corps attracteur est le corps autour duquel un autre corps gravite.
Remarque : Dans le cas de Jupiter, le corps attracteur est le Soleil.
Seconde loi. (La loi des aires)
En des temps égaux, le rayon vecteur balaie la même aire.
Comprenons cette énoncé. Revenons à notre exemple sur Jupiter.
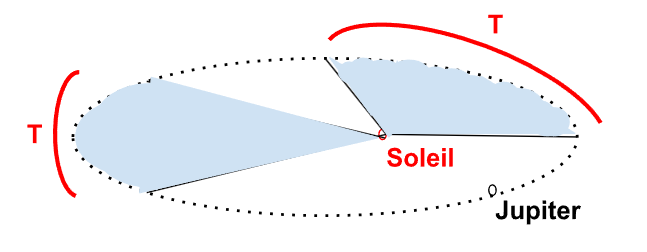
Figure 3. - Représentation de la seconde loi de Kepler pour Jupiter
En notant \(T\) une durée alors les aires balayées durant cette durée sont égales, ainsi les deux aires dessinées sont égales car elles ont été mesurées durant la même durée. Une conséquence de ce résultat est qu'il existe un lien entre la distance entre la position de Jupiter au Soleil et la vitesse de Jupiter : plus la position de Jupiter au Soleil est petite, plus la vitesse de Jupiter est grande.
Remarque : La preuve de ce résultat résulte du fait que dans un mouvement conservatif, une grandeur se conserve, elle est appelée constante des aires. Elle dépend de la vitesse de rotation de corps et de sa distance à son corps attracteur.
2.3. Troisième loi de Kepler ou loi des périodes
Définition 5. (La période de révolution)
Dans le cas d'un mouvement elliptique, c'est le temps mis par l'astre pour parcourir l'orbite une fois.
Troisième loi. (La loi des périodes)
Dans le cadre d'un mouvement supposé circulaire, en notant \(r\) le rayon de la trajectoire et \(T\) la période de révolution sur cette orbite alors, le carré de la période \(T\) est proportionnelle au cube du rayon \(r\) :
Preuve
Le résultat se devine à partir du résultat obtenu au paragraphe § 1.2. En reprenant les notations de la section 1, la vitesse d'un objet céleste \(A\) est donnée par l'expression : \[ v_A=\sqrt{\frac{GM_O}{r}} \] où \(M_O\) est la masse du corps attracteur de \(A\) et \(r\) le rayon de sa trajectoire. Comme la vitesse, dans ce cas, a été démontrée constante en 1.1., on peut la calculer en considérant que c'est le rapport entre la distance parcourue par l'astre \(A\) durant sa période de révolution notée \(T_A\). Par définition, cela correspond à une distance égale à la longueur de l'orbite supposée circulaire d'où : \[ v_A=\frac{2\pi r}{T_A} \] ce qui conduit à l'égalité suivante : \[ \frac{GM_O}{r}=\frac{4\pi^2 r^2}{T_A^2} \] d'où, \[ \frac{T_A^2}{r^3}=\frac{4\pi^2}{GM_O} \] D'une part, le rapport \(\frac{T_A^2}{r^3}\) est constant et d'autre part, la constante \(C\) est définie comme : \[ \frac{T_A^2}{r^3}=C \quad \textrm{avec}\quad C=\frac{4\pi^2}{GM_O} \]
Troisième loi. (La loi des périodes - dans le système solaire)
En utilisant les notations de l'énoncé précèdent et en supposant que le corps attracteur est le Soleil de masse \(M_\odot\) alors :
Définition 6. (La période de rotation)
Le période de rotation correspond à la durée que met un astre pour effectuer un tour sur lui-même.
Remarque : Par exemple, la période de rotation de la Terre est environ égale à 23 h 56 min 04 s.
Définition 7. (Les orbites géostationnaires)
Une orbite est dite géostationnaire lorsqu'elle permet à tout objet qui la possède comme orbite d'avoir une période de révolution égale à la période de rotation de la Terre.
Exercice.
Notons \(h\) l'altitude de cette orbite, \(M_T\) la masse de la Terre, \(R_T\) le rayon de la Terre et \(T_T\) la période de rotation de la Terre. Déterminer l'expression de l'orbite géostationnaire \(h\) en fonction de \(M_T\), \(T_T\) et \(R_T\).
Correction
Si l'on veut que l'orbite soit géostationnaire alors sa période de révolution qu'on notera \(T\) doit correspond à la période de rotation de la Terre donc : \[ T=T_T \] D'après la loi des périodes dans le cas où le corps attracteur est la Terre alors : \[ \frac{T^2}{(R_T+h)^3}=\frac{4\pi^2}{GM_T} \] en alliant les deux précédentes égalités, on obtient : \[ \frac{T_T^2}{(R_T+h)^3}=\frac{4\pi^2}{GM_T} \] d'où : \[ (R_T+h)^3=\frac{GM_TT_T^2}{4\pi^2} \] ce qui permet de retrouver \(h\) : \[ \boxed{h=\sqrt[3]{\frac{GM_TT_T^2}{4\pi^2}}-R_T} \]
Par application numérique, on obtient : \[ \boxed{h\approx 3,6.10^{4} \text{ km}} \] Bien que cette démonstration ne soit pas explicitement au programme, il est très recommandé de savoir comment l'on raisonne ici pour retrouver l'expression de \(h\) en utilisant la troisième loi de Kepler.
3. Point mathématique sur les ellipses
Cette section permet simplement d'observer d'un aspect plus mathématique la notion d'ellipses. Elle n'est pas inaccessible pour un élève de terminale, reste facultative mais très intéressante pour mieux comprendre les outils maniés dans ce chapitre. On la recommande vivement pour son paragraphe 3.1. qui permet d'assimiler des notions autour des ellipses qui, ici, sont exposées simplement. On pense par exemple à la notion de demi grand axe, demi petit axe, de foyers qui est au programme. La section 3.2. est elle réservée qu'à ceux qui ont déjà bien acquis des outils en mathématiques sur les équations différentielles et la dérivation.
3.1. Introduction aux ellipses
Définition 8. (Équation d'une ellipse)
Si une figure géométrique admet comme équation : \[ \left(\frac{x}{a}\right)^2+\left(\frac{y}{b}\right)^2=1 \textrm{ où } a^2>b^2>0 \] alors on dit que c'est une ellipse.
Remarque : Ainsi, on traduit toutes les ellipses par une équation mathématique.
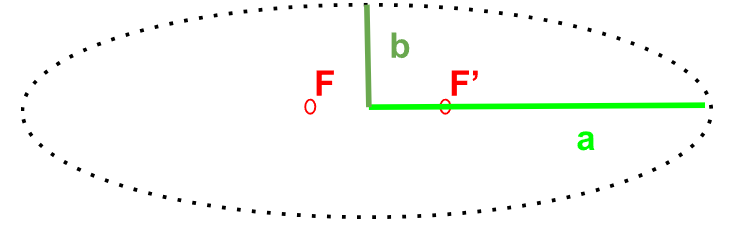
FIGURE 4 - Représentation géométrique d'une ellipse
La longueur \(a\) s'appelle demi grand axe, la longueur \(b\) demi petit axe. En utilisant ces notations, on peut réécrire (pour généraliser) la troisième loi de Kepler pour une orbite elliptique dans le système solaire :
On définit une nouvelle grandeur appelée excentricité de l'ellipse qui permet de voir à quel point une ellipse est allongée sur elle-même ou écartée sur elle-même pour ainsi se rapprocher d'un cercle.
Définition 9. (Excentricité d'une ellipse)
Soit une ellipse de demi grand axe \(a\) et de demi petit axe \(b\). On définit \(e\) comme l'excentricité de l'ellipse par la relation suivante : \[ e=\sqrt{a^2-b^2} \]
Remarque : Ainsi, l'excentricité \(e\) mesure bien à quel point l'ellipse est allongée sur elle-même.
Remarque : Quand \(e\) tend vers 1, l'ellipse se confond presque à une ligne. En revanche quand \(e\) tend vers 0, l'ellipse tend à devenir un cercle.
Propriété 1. (Aire d'une ellipse - HP)
Soit une ellipse de demi grand axe \(a\) et de demi petit axe \(b\). L'aire de cette ellipse notée \(\mathcal{A}\) est donnée par la relation :
Preuve
Le résultat n'est pas compliqué à démontrer. Il nécessite que de savoir les méthode pour intégrer une fonction continue. On sait qu'une ellipse de demi grand axe \(a\) et de demi petit axe \(b\) a pour équation : \[ \left(\frac{x}{a}\right)^2+\left(\frac{y}{b}\right)^2=1 \] avec \(a^2>b^2>0\). Ainsi, l'objectif est d'exprimer \(y\) en fonction de \(x\) comme suit: \[ y(x)=b\sqrt{1-\left(\frac{x}{a}\right)^2} \] Maintenant, intégrons \(y\) entre \(-a\) et \(a\) pour obtenir \(\frac{\mathcal{A}}{2}\): \[ \begin{align*} \frac{\mathcal{A}}{2}&=\int_{-a}^{a}b\sqrt{1-\left(\frac{x}{a}\right)^2}dx\\ &=2b\int_{0}^{a}\sqrt{1-\left(\frac{x}{a}\right)^2}dx \quad \textrm{car $y$ est paire} \end{align*} \] \[ \begin{align*} &=2ab\int_{0}^{1}\sqrt{1-u^2}du \quad \quad \textrm{en posant le changement de variable $u=\frac{x}{a}$} \end{align*} \] (Note : \(dx\) devient \(a \, du\))
Or, si l'on observe bien, l'intégrale \(\int_{0}^{1}\sqrt{1-u^2}du\) correspond à calculer le quart de l'aire (quart haut droit) d'un cercle de rayon 1 et de centre (0,0). Cette aire correspond à \(\frac{\pi}{4}\) d'où : \[ \frac{\mathcal{A}}{2}=2ab\times \frac{\pi}{4} \] il en résulte alors, \[ \boxed{\mathcal{A}=\pi ab} \]
Définition 10. (L'ellipse - une seconde définition)
L'ellipse est la seule figure du plan telle qu'il existe deux points uniques \(F\) et \(F'\) et pour tout point \(M\) sur l'ellipse, la distance \(FM+F'M\) est toujours constante. On appelle cette distance, la distance bifocale de l'ellipse.
Remarque : Les points \(F\) et \(F'\) ont été représentés sur la figure 4. Pour faire l'analogie au cours, le corps attracteur occupe l'un des deux foyers.
Propriété 2. (La valeur de la distance bifocale)
Soit une ellipse de demi grand axe \(a\) et de demi petit axe \(b\). La distance bifocale vaut \(2a\).
Preuve
Dans une ellipse, la distance bifocale est constante. Prenons le cas particulier où \(M\) est placé dans l'une des deux intersections produites par l'ellipse et la droite passant par \(F\) et \(F'\). On fixe dans notre cas : \[ FM=a-\frac{FF'}{2} \] alors, on a directement que : \[ F'M=a+\frac{FF'}{2} \] Par somme, il en suit que : \[ \boxed{FM+F'M=2a} \]
3.2. Application à l'étude des orbites (HP+)
L'objectif de cette section est de ne plus supposer que la distance \(r\) entre \(O\) et \(A\) de la section 1 est constante mais qu'elle varie dans le temps, on la notera alors \(r(t)\). Ainsi, on pourra prouver la première loi de Kepler, celle qui énonce que les corps célestes ont une trajectoire elliptique autour de leur corps attracteur.
On admettra aussi l'expression généralisée de l'accélération de \(A\) dans ce qu'on appelle le repère de Frenet pour un mouvement curviligne : \[ \vec{a}_A(t)=(r(t)\dot{\theta}^2(t)-\ddot{r}^2(t))\vec{n}-(r(t)\ddot{\theta}+2\dot{r}(t)\dot{\theta}(t))\vec{t} \] où \(\theta\) désigne l'angle entre l'axe \(x\) et l'axe engendrée par le vecteur normal \(\vec{n}\). Le principe fondamental de la dynamique écrit en (1) permettait d'établir que suivant \(\vec{t}\), il n'y a aucune force : \[ (r(t)\ddot{\theta}+2\dot{r}(t)\dot{\theta}(t))\vec{t}=\vec{0} \] Or on remarque que : \[ \frac{d(r^2\dot{\theta})(t)}{dt}=2r(t)\dot{r}(t)\dot{\theta}(t)+r^2(t)\ddot{\theta}(t)=r(r(t)\ddot{\theta}+2\dot{r}(t)\dot{\theta}(t))=0 \] donc le terme \(r^2\dot{\theta}\) est constant au cours du temps. C'est ce terme là qu'on appelle \(\boxed{\textrm{constante des aires}}\), qu'on note \(\mathcal{C}\) et qui est à l'origine de la loi des aires.
D'autre part, le principe fondamental de la dynamique en projection suivant \(\vec{n}\) permet aussi d'écrire : \[ r(t)\dot{\theta}^2(t)-\ddot{r}^2(t)=G\frac{M_O}{r^2(t)} \] Dès à présent, on omettra d'indiquer la dépendance au temps pour la distance \(r\) et l'angle \(\theta\) pour améliorer la lisibilité des calculs mais on retiendra que \(r\) et \(\theta\) n'est pas constant au cours du temps. Ainsi, on peut réécrire l'équation précédente comme : \[ r\dot{\theta}^2-\ddot{r}^2=G\frac{M_O}{r^2} \] On réalise le changement de variable suivant valide car \(r\ne0\): \[ u=\frac{1}{r} \] en calculant les dérivées successives de \(u\), on a : \[ \dot{u}=-\frac{\dot{r}}{r^2} \quad \textrm{et} \quad \ddot{u}=-\frac{\ddot{r}r^2-2\dot{r}^2r}{r^4} \] Cherchons à établir une équation différentielle sur \(u\). On rappelle qu'on note \(\mathcal{C}\) la quantité constante : \[ \mathcal{C}=r^2\dot{\theta} \] d'où l'équation différentielle sur \(r\) devient : \[ \frac{\mathcal{C}^2}{r^3}-\ddot{r}^2=G\frac{M_O}{r^2} \] D'une part, on a : \[ \ddot{r}=\frac{2}{u^3}\dot{u}^2-\frac{1}{u^2}\ddot{u} \] il en résulte alors d'après l'équation sur \(r\), l'équation sur \(u\) suivante : \[ \frac{2}{u^3}\dot{u}^2-\frac{1}{u^2}\ddot{u}-\mathcal{C}^2u^3=-GM_Ou^2 \] Ici, \(u\) dépend du temps \(t\). Pour trouver l'expression de \(u\), il faut se ramener à une fonction \(u\) qui dépend de l'angle \(\theta\), ainsi on pose : \[ u'=\frac{du}{d\theta} \quad \textrm{et} \quad u''=\frac{d^2u}{d\theta^2} \] ainsi, on a : \[ \dot{u}=\frac{du}{dt}=\frac{du}{d\theta}\times\frac{d\theta}{dt}=u'\mathcal{C}u^2 \] et on a aussi : \[ \begin{align*} \ddot{u}&=\frac{d^2u}{dt}=\frac{d}{dt}\left(u'\mathcal{C}u^2\right)\\ &=\frac{du'}{dt}\mathcal{C}u^2+2\mathcal{C}u'\dot{u}u\\ &=\frac{du'}{d\theta}\times\frac{d\theta}{dt}\mathcal{C}u^2+2\mathcal{C}^2u'^2u^3\\ &=\mathcal{C}^2u^4u''+2\mathcal{C}^2u'^2u^3 \end{align*} \] Finalement, cela permet d'écrire : \[ \frac{2}{u^3}\left(u'\mathcal{C}u^2\right)^2-\frac{1}{u^2}\left(\mathcal{C}^2u^4u''+2\mathcal{C}^2u'^2u^3\right)-\mathcal{C}^2u^3=-GM_Ou^2 \] ce qui équivaut à : \[ 2u'^2\mathcal{C}^2u-\mathcal{C}^2u^2u''-2\mathcal{C}^2u'^2u-\mathcal{C}^2u^3=-GM_Ou^2 \] finalement, des termes se simplifient pour donner : \[ u''+u=\frac{GM_O}{\mathcal{C}^2} \] On reconnaît l'équation différentielle d'un oscillateur harmonique, la solution étant donnée par : \[ u:\theta\mapsto \frac{GM_O}{\mathcal{C}^2}\left(A\cos(\theta-\theta_0)+1\right) \] avec \(A\) une constante à déterminer en fonction des conditions initiales.
En revenant à notre changement de variable, on en déduit que : \[ r:\theta\mapsto \frac{\mathcal{C}^2}{GM_O}\frac{1}{1+A\cos(\theta-\theta_0)} \] On peut montrer que \(A\in[0,1]\), la trajectoire des astres soumis à l'attraction gravitationnelle est bien une ellipse. On peut même prouver que \(A\) n'est rien de plus que l'excentricité de l'ellipse qu'on note habituellement \(e\) et c'est ainsi qu'on trouve :
Pour résumé, nous avons démontré la première loi de Kepler.