Terminale : Mouvement dans un champs uniforme
Le symbole ❤️ à côté d'un titre d'une nouvelle section indique que la méthode développée dans la suite est à savoir refaire SANS ERREUR.
📚 Table des matières
1. Rappels sur les champs gravitationnel et électrique
Rappelons dans cette première section des notions qui ont été évoquées dans le cours sur la dynamique du point matériel : le champ de pesanteur aussi appelé champ gravitationnel engendré par un point matériel de masse \(M\) et le champ électrique engendré par une particule chargée de charge \(Q\).
Définition 1. (Expression du champ gravitationnel - champ de gravité ou champ de pesanteur)
Soit \(A\) un point matériel de masse \(M\). Le champ gravitationnel ou champ de gravité ou champ de pesanteur qu'exerce le point \(A\) sur un point quelconque de l'espace \(B\) prend la forme vectorielle suivante :
Remarque : Ici, le champ de pesanteur est défini comme un champ attractif du fait qu'il y a un moins dans son expression.
Définition 2. (Expression du champ électrique ou champ électrostatique)
Soit \(A\) un point chargé de charge \(Q\). Le champ électrique ou champ électrostatique qu'exerce le point \(A\) sur un point quelconque de l'espace \(B\) prend la forme vectorielle suivante :
Remarque : Ici, on ne pourra pas conclure sur le caractère attractif ou répulsif du champ électrique étant donné qu'il dépend à la fois du signe de la charge du point \(A\) et du signe de la charge du point \(B\).
L'intérêt d'évoquer ces champs est qu'ils permettent de définir les forces gravitationnelle et électrique ressenties en un point de l'espace. On résume ce qui a été fait dans le cours sur la dynamique du point matériel :
Définition 3. (Expression de la force gravitationnelle)
Soient \(A\) et \(B\) deux points matériels respectivement de masse \(M\) et de masse \(m\). La force gravitationnelle qu'exerce le point \(A\) sur le point \(B\) prend la forme vectorielle suivante :
Remarque : Le principe des actions réciproques permet de retrouver l'expression de \(\vec{F}_B(A)\).
Définition 4. (Expression de la force électrique)
Soient \(A\) et \(B\) deux particules chargées respectivement de charge \(Q\) et de charge \(q\). La force électrique qu'exerce le point \(A\) sur le point \(B\) prend la forme vectorielle suivante :
Remarque : Le principe des actions réciproques permet de retrouver l'expression de \(\vec{F}_B(A)\).
De la définition 3, on retrouve la définition du poids :
Définition 5. (Expression du poids)
Soit \(O\) un point d'altitude \(h\) faible devant le rayon terrestre et de masse \(m\) et \(O_T\) le centre de masse de la Terre. Le poids de \(O\) sur Terre est défini comme :
Avec ces outils et tous les autres vus dans les cours de cinématique et dynamique, on peut mener à bien les problèmes de mécanique qui suivront.
2. Mouvement dans un champ de pesanteur uniforme ❤️
L'objectif ici est d'introduire un problème de mécanique qui modélise le lancer d'un objet. Nous verrons comment le mettre en équations puis observerons l'allure de sa trajectoire et calculerons la distance qu'il pourrait parcourir ainsi que la hauteur maximale qu'il pourrait atteindre.
2.1. Étude d'un tir de projectile
Ici, on considère un projectile repéré par un point \(M\) de masse \(m\) lancé à une vitesse \(V_0\) dans une direction depuis une hauteur \(h\) et qui forme un angle \(\alpha\) avec l'horizontal.
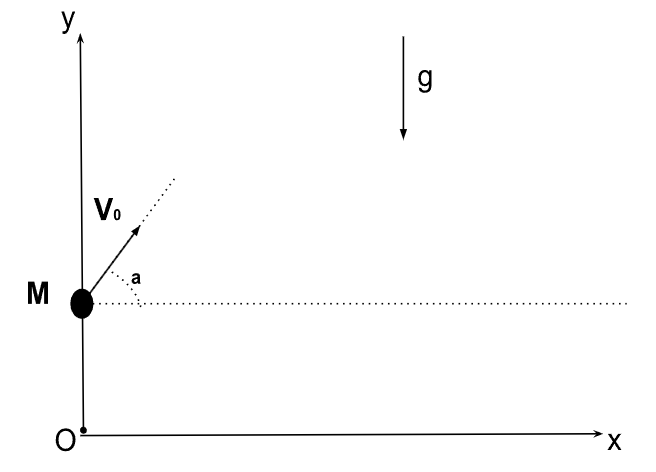
Figure 1. Modélisation du problème du projectile lancé
2.2. Équations horaires du mouvement
Définissons notre système : {projectile}. Plaçons nous dans un référentiel adapté à notre problème, choisissons le référentiel terrestre supposé galiléen. Si l'on réalise le bilan des actions extérieures qui s'exercent sur notre système, il n'y a que le poids et les frottements. Ici, nous ferons la première hypothèse : les frottements ne seront pas pris en compte dans l'étude mécanique du système.
Ainsi, le principe fondamental de la dynamique permet alors d'écrire, si l'on note \(\vec{a}\) l'accélération du système et \(\vec{P}\) son poids : \[ m\vec{a}=\vec{P} \] or, en projetant sur nos axes du plan cette relation vectorielle : \[ m\left(\frac{d^2x}{dt^2}\vec{u}_x+\frac{d^2y}{dt^2}\vec{u}_y\right)=-mg\vec{u}_y \] par identification, on en déduit le système suivant : \[ \left \{ \begin{array}{c @{=} c} \frac{d^2x}{dt^2} & 0 \\ \frac{d^2y}{dt^2} & -g \end{array} \right. \quad (1) \] Ici, on observe que peu importe la masse du système considéré, la Terre nous fait subir la même accélération. Autrement dit, deux objets de masses différentes, lorsqu'on ne considère pas les frottements, tombent à la même vitesse. Enfin, sans rentrer dans les détails physiques du calcul, la masse mise en jeu dans la force gravitationnelle s'appelle la masse gravitationnelle et la masse mise en jeu dans le principe fondamental de la dynamique s'appelle la masse inertielle. Il n'est pas trivial de supposer que les deux sont égales MAIS l'expérience a permis de montrer que ces deux masses sont égales.
Avant de poursuivre, il est recommandé d'aller consulter la fiche qui donne les méthodes pour intégrer des fonctions. Intégrons alors les expressions données par le système précédent : \[ \left \{ \begin{array}{c @{=} c} \frac{dx}{dt} & A \\ \frac{dy}{dt} & -gt+B \end{array} \right. \] où \(A\) et \(B\) sont deux constantes à déterminer. À l'instant initial, \(v(0)=V_0\) donc en projetant \(\vec{V}_0\) sur les axes \(x\) et \(y\) on pourra déterminer les constantes \(A\) et \(B\). D'après les relations trigonométriques, on a : \[ \left \{ \begin{array}{c @{=} c} A & V_0\cos(\alpha) \\ B & V_0\sin(\alpha) \end{array} \right. \] On en déduit alors l'écriture suivante : \[ \left \{ \begin{array}{c @{=} c} \frac{dx}{dt} & V_0\cos(\alpha) \\ \frac{dy}{dt} & -gt+V_0\sin(\alpha) \end{array} \right. \quad (2) \] Intégrons à nouveau ce système pour obtenir les équations horaires liées aux positions \(x\) et \(y\). \[ \left \{ \begin{array}{c @{=} c} x & V_0\cos(\alpha)t+C \\ y & -\frac{g}{2}t^2+V_0\sin(\alpha)t+D \end{array} \right. \] où \(C\) et \(D\) sont à nouveau deux constantes à déterminer. On utilise à nouveau les conditions initiales, le projectile est, à l'état initial, à la position \((0,h)\). Il en suit que : \[ \left \{ \begin{array}{c @{=} c} C & 0 \\ D & h \end{array} \right. \] finalement, on a : \[ \left \{ \begin{array}{c @{=} c} x & V_0\cos(\alpha)t \\ y & -\frac{g}{2}t^2+V_0\sin(\alpha)t+h \end{array} \right. \quad (3) \] ce sont les équations horaires du mouvement.
2.3. Détermination de l'équation de la trajectoire
Dans les équations horaires du mouvement, \(x\) et \(y\) dépendent du temps \(t\). Pour trouver l'équation du mouvement, il faut basculer ces écritures en une écriture qui relie \(y\) à \(x\). On peut écrire, pour \(\alpha \ne \frac{\pi}{2}\) : \[ \left \{ \begin{array}{c @{=} c} t & \frac{x}{V_0\cos(\alpha)} \\ y & -\frac{g}{2}t^2+V_0\sin(\alpha)t+h \end{array} \right. \] Finalement, en remplaçant \(t\) par son expression en fonction de \(x\) dans \(y\), on en déduit l'équation de la trajectoire : \[ \begin{align*} y &= -\frac{g}{2}\left(\frac{x}{V_0\cos(\alpha)}\right)^2+V_0\sin(\alpha)\frac{x}{V_0\cos(\alpha)}+h\\ &=-\frac{g}{2V_0^2\cos^2(\alpha)}x^2+\tan(\alpha)x+h \end{align*} \] Mathématiquement, on vient de retrouver l'équation d'une parabole, on en déduit alors le dessin suivant de la trajectoire :
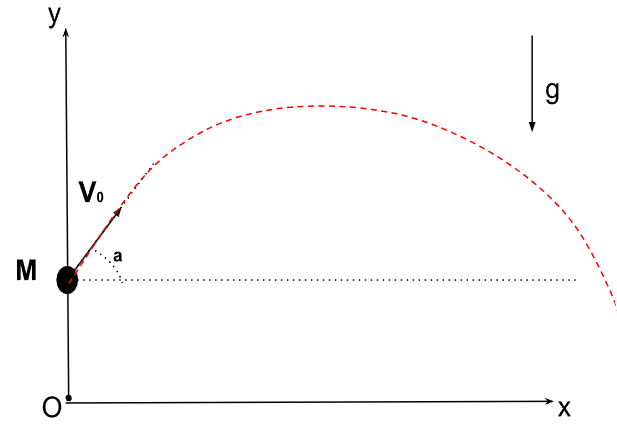
Figure 2. Représentation de la trajectoire réelle que doit suivre \(M\) en absence de frottements
On voit la cohérence entre la réalité et la théorie. Dans la vraie vie, un projectile suit bien une trajectoire parabolique si l'on néglige les frottements à sa surface.
2.4. Notion de portée et de flèche
Définition 6. (La portée)
La portée correspond à la distance parcourue horizontalement par le système avant qu'il touche le sol pour la première fois.
Définition 7. (La flèche)
La flèche correspond à l'altitude maximale atteinte par le système au cours de son mouvement.
Méthode
- Pour trouver la portée d'un système \(\mathcal{S}\), il faut trouver la solution positive solution de l'équation : \(y(x)=0\).
- Pour trouver la flèche d'un système \(\mathcal{S}\), il suffit de trouver l'instant \(t_0\) qui correspond à l'instant à lequel la vitesse suivant l'axe \(y\) est nulle. Ensuite, \(y(t=t_0)\) correspond à la flèche.
Raisonnons à l'aide de la méthode pour trouver la portée qu'on notera \(x_p\) et la flèche qu'on notera \(y_f\).
Reprenons l'équation de la trajectoire pour trouver \(x_p\) : \[ y(x_p)=0\iff -\frac{g}{2V_0^2\cos^2(\alpha)}x_p^2+\tan(\alpha)x_p+h=0 \] Le discriminant de cette équation polynomiale, notée \(\Delta\) est égal : \[ \Delta=\tan^2(\alpha)+\frac{2gh}{V_0^2\cos^2(\alpha)}=\frac{V_0^2\sin^2(\alpha)+2gh}{V_0^2\cos^2(\alpha)} \] Les racines \(x_-\) et \(x_+\) correspondent : \[ x_-=\frac{\tan(\alpha)-\sqrt{\frac{V_0^2\sin^2(\alpha)+2gh}{V_0^2\cos^2(\alpha)}}}{\frac{g}{V_0^2\cos^2(\alpha)}} \] et, \[ x_+=\frac{\tan(\alpha)+\sqrt{\frac{V_0^2\sin^2(\alpha)+2gh}{V_0^2\cos^2(\alpha)}}}{\frac{g}{V_0^2\cos^2(\alpha)}} \] dès lors, on peut (par le calcul) directement remarquer que \(x_- \leq 0\). Ainsi, \(x_p=x_+\). D'où, \[ x_p=\frac{V_0\cos(\alpha)\left(V_0\sin(\alpha)+\sqrt{V_0^2\sin^2(\alpha)+2gh}\right)}{g} \] on retrouve un résultat classique pour \(h=0\) : \[ x_p(h=0)=\frac{2V_0^2\cos(\alpha)\sin(\alpha)}{g}=\frac{V_0^2\sin(2\alpha)}{g} \] Ainsi, on en déduit qu'à \(h=0\) (projectile initialement au sol), la portée est maximale suivant \(\alpha=\frac{\pi}{4}\), autrement-dit pour parcourir une distance plus grande, le projectile doit être lancé avec une inclinaison égale à \(\frac{\pi}{4}\).
Déterminer l'expression de \(y_f\). On cherche alors \(t_0\) tel que : \[ \frac{dy}{dt}(t_0)=0\iff \underbrace{t_0=\frac{V_0\sin(\alpha)}{g}}_{\textrm{d'après (2)}} \] Or, la méthode fournit que : \(y_f=y(t_0)\) donc en utilisant (3), \[ y_f=y(t_0)=-\frac{g}{2}t_0^2+V_0\sin(\alpha)t_0+h \] en développant, on récupère : \[ \begin{align*} y_f&=-\frac{g}{2}\frac{V_0^2\sin^2(\alpha)}{g^2}+V_0\sin(\alpha)\frac{V_0\sin(\alpha)}{g}+h\\ &=\frac{V_0^2\sin^2(\alpha)}{2g}+h \end{align*} \] C'est l'expression de la flèche. Attention, elle prend en compte l'altitude \(h\) initiale. La méthode est à retenir étant donné qu'elle fait l'objet habituellement de questions au BAC. Les expressions, quand à elles, ne sont pas à connaître, il faut juste savoir les retrouver !
Finalement, on a réussi à exprimer la portée et la flèche dans notre problème de mécanique.
3. Mouvement dans un champ électrique uniforme ❤️
Voici une section plus délicate car elle fera moins l'objet de notre intuition physique étant donné que les phénomènes mis en jeu ne sont pas observables dans notre quotidien (sauf si l'on travaille dans la recherche). Il faudra alors être très rigoureux dans les calculs, vérifier que ce que l'on écrit à un sens physique (vérification de la dimension de notre calcul, respect des unités...) et tenter de trouver de simples interprétations de ces phénomènes pour retenir plus facilement le schéma de résolution.
3.1. Étude d'une particule dans un condensateur plan
L'objectif ici, est d'étudier comment une particule chargée de charge \(q\) se comporte en passant à travers un condensateur plan. Ici, nous allons définir le condensateur plan mais il est vivement recommandé d'aller consulter le cours d'électrocinétique pour mieux comprendre ce dipôle électrique.
Définition 8. (Le condensateur)
Un condensateur est un dipôle électrique constitué de deux armatures conductrices parallèles séparées par un composant diélectrique, l'équivalent d'un isolant. Lorsqu'il est alimenté par un courant, l'une des plaques accumule des charges positives et l'autre des charges négatives.
On définira \(Q>0\) comme étant la charge positive du condensateur ainsi une des deux armatures a pour charge \(+Q\) et l'autre \(-Q\), la charge portée étant fixée par le sens du courant. Voici un schéma du dispositif :
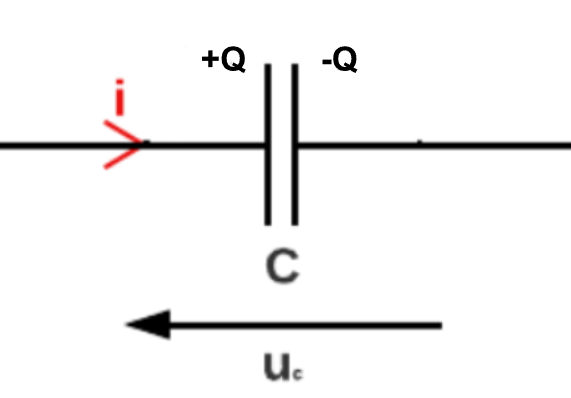
Figure 3. Schéma d'un condensateur plan
avec \(u_c\) la tension aux bornes du condensateur et \(i\) l'intensité du courant qui le parcourt.
On se place dans la situation suivante :
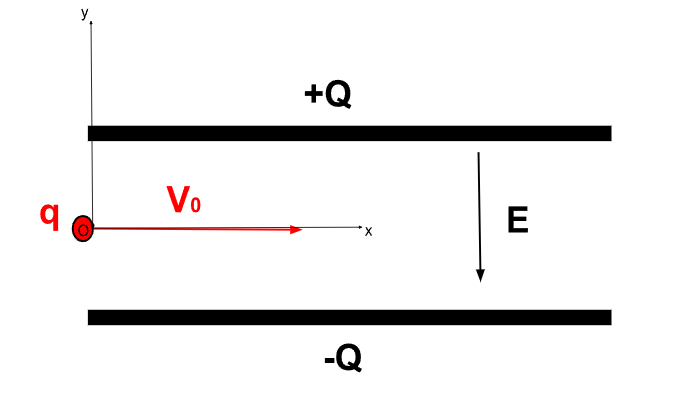
Figure 4. Schéma de la situation considéré
Pour résumer, on considère une particule qui arrive à l'entrée d'un condensateur à une vitesse \(\vec{v}_0\) horizontale. On notera dans la suite \(\vec{E}\) le champ électrique généré par le condensateur entre ses armatures, \(L\) la longueur de ses plaques d'épaisseur négligé et de largeur non considéré pour la suite. On suppose que la particule à l'entrée a une charge \(q\) de signe non définie pour l'instant.
Remarque : Nous verrons à la fin du problème l'expression de la norme du champ \(\vec{E}\) en fonction de la tension \(u_c\) et de la distance entre les deux armatures notée \(d\). Cette relation nous sera utile si l'on veut calculer le champ \(\vec{E}\) en tout point (supposé uniforme dans toute la suite).
Notre système est la particule de charge \(q\). On se place dans le référentiel terrestre (on pourrait, rigoureusement, se placer au référentiel lié au laboratoire galiléen dans la suite) supposé galiléen. Le bilan des actions mécaniques qui s'exercent sur notre système est le poids et la force électrique. On pourrait le vérifier mais à ses échelles (microscopique), la norme du poids est très petite devant celle liée à la force électrique. On supposera alors que la seule force qui intervient en partie dans la description du mouvement est la force électrique.
Remarque : Les frottements à cette échelle continuent d'exister. Il existe des forces qui à cette échelle pourrait faire vibrer la particule, la faire légèrement dévier MAIS leur norme est insignifiante devant celle liée à la force électrique. C'est pour cela qu'on ne les prend pas en compte.
3.2. Équations horaires du mouvement
Le principe fondamental de la dynamique appliqué à la particule dans le référentiel terrestre permet d'écrire : \[ m\vec{a}=\vec{F}_{el} \] où \(\vec{a}\) désigne l'accélération de la particule, \(m\) sa masse (très faible) et \(\vec{F}_{el}\) la force électrique que subit la particule. D'après la définition 4, on peut écrire : \[ \vec{F}_{el}=q\vec{E} \] Si l'on définit un repère plan d'axe \(x\) et \(y\), l'axe \(x\) étant l'horizontale et l'axe \(y\) la verticale avec comme origine, la position initiale de la particule alors, par projection, on obtient : \[ m\left(\frac{d^2x}{dt^2}\vec{u}_x+\frac{d^2y}{dt^2}\vec{u}_y\right)=-qE\vec{u}_y \] avec \(E\) la norme de \(\vec{E}\). Par identification, on en déduit le système suivant : \[ \left \{ \begin{array}{c @{=} c} \frac{d^2x}{dt^2} & 0 \\ \frac{d^2y}{dt^2} & -\frac{qE}{m} \end{array} \right. \] La particule ne subit alors qu'une accélération vers le bas car il y a un champ électrique. En intégrant ce système, on obtient : \[ \left \{ \begin{array}{c @{=} c} \frac{dx}{dt} & A \\ \frac{dy}{dt} & -\frac{qE}{m}t+B \end{array} \right. \] avec \(A\) et \(B\) deux constantes à déterminer. Comme la vitesse initiale \(\vec{v}_0\) n'est que suivant l'horizontale (cf. figure 4), on en déduit que : \[ \left \{ \begin{array}{c @{=} c} \frac{dx}{dt} & v_0 \\ \frac{dy}{dt} & -\frac{qE}{m}t \end{array} \right. \] en intégrant à nouveau, il existe alors \(C\) et \(D\) deux nouvelles constantes telles que : \[ \left \{ \begin{array}{c @{=} c} x & v_0t+C \\ y & -\frac{qE}{2m}t^2+D \end{array} \right. \] mais avec le fait qu'à l'état initial, la position de la particule est confondu avec l'origine alors : \[ \left \{ \begin{array}{c @{=} c} x & v_0t \\ y & -\frac{qE}{2m}t^2 \end{array} \right. \]
Ces résultats bien qu'inutiles pour l'instant ont un intérêt si l'on veut pousser plus loin l'exercice. Après avoir déterminé ces équations, on pourrait déterminer la vitesse en sortie du condensateur atteinte par la particule suivant l'axe \(x\) et suivant l'axe \(y\). On pourrait aussi calculer de combien la trajectoire a été déviée le long de la traversée en se ramenant à un problème d'angle géométrique. On pourrait aussi se placer dans la situation où on place un écran à une distance \(e\) de la sortie du condensateur et on détermine la position du point d'impact de la particule sur l'écran. Tous ces scénarios seront disponibles dans le TD.
Discutons de l'expression de la norme du champ électrique \(\vec{E}\) en fonction de la tension \(u_c\) et de la distance entre les armatures notée \(d\).
Propriété 1. (Expression du champ électrique dans un condensateur)
Soient \(u_c\) la tension supposée constante aux bornes d'un condensateur, \(d\) la distance entre ses armatures et \(E\) la norme du champ électrique généré dans le condensateur. La norme du champ \(\vec{E}\) est définie comme :
Preuve (HP)
Démontrons ce résultat. La force électrique \(\vec{F}_{el}\) est une force conservative, on peut alors lui associer une énergie potentielle \(E_p\) : \[ \vec{F}_{el}.d\vec{l}=-dE_p \] où \(d\vec{l}\) est le déplacement élémentaire. Autrement dit, toute force conservative dérive d'une énergie potentielle. Utilisons la relation qu'on admet : \[ \vec{E}=-\frac{dV}{dx}\vec{u}_y \] On retrouve bien que \(\vec{E}\) est orienté de l'armature positive à l'armature négative. Si l'on discrétise cette expression, on déduit que : \[ \boxed{E=\frac{u_c}{d}} \] ce qui achève cette démonstration.
4. Aspect énergétique lié au champ uniforme
Cette section sera courte mais permettra d'appliquer les outils vus dans le cours sur l'approche énergétique du mouvement à l'étude d'une particule dans un champ gravitationnel ou dans un champ électrique. Nous évoquerons la notion d'énergie potentielle dans chacun de ces champs puis nous approfondirons notre étude en nous concentrant sur les champs électriques. Une remarque sera faite pour étendre les résultats obtenus aux champs gravitationnels. Nous parlerons aussi au passage de la notion de potentiel électrique ou encore potentiel électrostatique qui se définit à partir du champ électrique.
4.1. Énergie potentielle de pesanteur
Définissons dans cette section, l'énergie potentielle liée à l'attraction gravitationnelle sur Terre.
Propriété 2. (Expression de l'énergie potentielle de pesanteur - cas uniforme)
Soit \(A\) un point matériel de masse \(m\) d'altitude \(z\) par rapport au sol et on note traditionnellement \(g\) l'intensité de pesanteur. En notant \(E_{pp}\) l'énergie potentielle de pesanteur de \(A\) alors :
4.2. Énergie potentielle électrique
Dans ce paragraphe, on définit une façon de déterminer l'énergie acquise par une particule chargée de charge \(q\) dans un champ électrique sur un trajet reliant \(A\) à \(B\). Rappelons que peu importe le trajet choisi par la particule, comme la force électrique est conservative, cette énergie acquise est la même sur tout trajet.
Propriété 3. (Expression de l'énergie potentielle électrique - cas uniforme)
Soient \(A\) et \(B\) deux points et \(\vec{E}\) le champ électrique supposé uniforme. En notant \(\Delta_{A\rightarrow B}E_{p_{el}}\) la variation d'énergie potentielle électrique d'une particule chargée de charge \(q\) entre \(A\) et \(B\) alors :
Remarque : On appelle potentiel électrique en électrocinétique, la grandeur qui mesure l'énergie potentielle électrique par unité de charge. Cela correspond bien à la relation précédente liant l'énergie potentielle électrique \(E_{p_{el}}\), \(q\) la charge et le potentiel. En fait, le potentiel noté \(V\) en général définit la tension mais se définit grâce au champ électrique, c'est ce qui est à retenir.
4.3. Théorème de l'énergie cinétique dans un champ électrique
Dans ce paragraphe, on réécrit le théorème de l'énergie cinétique dans le cas où on est plongé dans un champ électrique uniforme seulement (absence de champ gravitationnel par exemple).
Propriété 4. (Théorème de l'énergie cinétique en présence seul d'un champ électrique uniforme)
Soient \(A\) et \(B\) deux points et \(\vec{E}\) le champ électrique supposé uniforme. En notant \(\Delta_{A\rightarrow B}E_c\) la variation d'énergie cinétique d'une particule chargée de charge \(q\) entre \(A\) et \(B\) alors :
Remarque : Il est bien entendu normal que le théorème de l'énergie cinétique (propriété 4) et celui énoncé à la propriété 3 s'opposent dans leur écriture car comme la force électrique est conservative alors en notant \(E_m\) l'énergie mécanique de la particule chargée, avec les mêmes notations que précédemment, on a : \[ \Delta_{A\rightarrow B}E_m=0 \] or en présence d'un champ électrique seul, on peut aussi écrire : \[ \Delta_{A\rightarrow B}E_m=\Delta_{A\rightarrow B}E_c+\Delta_{A\rightarrow B}E_{p_{el}} \] donc le principe 4 se déduit du principe 3 et inversement. Ils sont équivalents grâce au théorème de l'énergie mécanique en présence seul d'un champ électrique uniforme. On aurait pu réécrire tous ces résultats dans le cas où il y a seulement un champ gravitationnel mais ces résultats sont plus simples à deviner. En effet, dans le cas où \(A\) et \(B\) représentent deux points et \(\vec{g}\) le champ gravitationnel supposé uniforme alors : \[ \Delta_{A\rightarrow B}E_c=m(z_A-z_B)g \] où \(m\) correspond à la masse de notre système, \(z_A\) à l'altitude de \(A\) et \(z_B\) à l'altitude de \(B\). Par opposition, si l'on note à nouveau \(E_m\) l'énergie mécanique de notre système mécanique alors, \[ \Delta_{A\rightarrow B}E_m=0 \] donc la variation d'énergie potentielle de pesanteur s'écrit : \[ \Delta_{A\rightarrow B}E_{pp}=-m(z_A-z_B)g \]