Terminale : Exercices sur le mouvement dans un champ uniforme
La mention ❤️ indique que la méthode de résolution proposée par l'exercice est à maîtriser et à savoir refaire, on peut aussi parler d'exercice classique. Finalement, chaque exercice possède sa propre difficulté : 🌶️ pour un exercice facile, 🌶️🌶️ pour un exercice de difficulté moyenne et 🌶️🌶️🌶️ pour un exercice difficile dans sa résolution.
Exercices d'application
Exercice 1 (Maximisation de la portée) ❤️ 🌶️ 🌶️ 🌶️
Ici, on considère un projectile repéré par un point \(M\) de masse \(m\) lancé à une vitesse \(V_0\), qui forme un angle \(\alpha\) avec l'horizontal, depuis une hauteur \(h\).
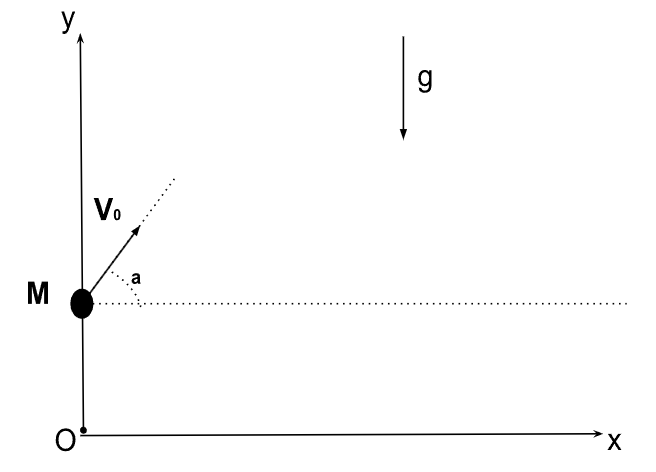
1. Définir le système étudié et le référentiel d'étude approprié.
2. En négligeant la poussée d'Archimède subie par le projectile, montrer que : \[ \vec{a}_x=\vec{0} \quad \textrm{et} \quad \vec{a}_y=\vec{g} \] (Note: l'équation LaTeX \(\vec{a}_y=\vec{g}\) suppose un axe \(y\) vers le bas. L'image `plan project.png` montre un axe \(y\) vers le haut. Nous suivrons l'image pour les indices, mais la question est posée telle quelle.)
3. Déterminer alors les équations horaires du mouvement.
4. Déterminer l'équation de la trajectoire. Comment appelle-t-on ce type de trajectoire ?
5. Montrer que le projectile ne retombe que s'il vérifie la condition suivante : \[ \frac{V_0^2\sin^2(\alpha)+2gh}{V_0^2\cos^2(\alpha)}>0 \]
6. En supposant dans toute la suite que \(h=0\), montrer que l'expression de la portée est donnée par : \[ x_p(h=0)=\frac{V_0^2\sin(2\alpha)}{g} \] (Indication : pour tout \(x\) réel, \(\sin(2x)=2\cos(x)\sin(x)\))
7. Pour quelle valeur d'angle \(\alpha\), la portée est maximale ?
8. Au niveau de la flèche, que dire de la vitesse verticale ?
9. Montrer que l'expression de la flèche \(y_f\) dans le cas où la portée est maximale est la suivante : \[ y_f(h=0)=\frac{V_0^2}{2g} \]
Voir l'indice
1/2. Appliquez la 2ème loi de Newton (\(m\vec{a} = \sum \vec{F}\)) au système {projectile} dans le référentiel terrestre (galiléen). La seule force est le poids \(\vec{P} = m\vec{g}\). Projetez sur les axes \(x\) et \(y\) montrés sur l'image.
3. Intégrez deux fois les composantes de l'accélération. Utilisez les conditions initiales \(\vec{v}(0) = (V_0 \cos \alpha, V_0 \sin \alpha)\) et \(\overrightarrow{OM}(0) = (0, h)\).
4. Isolez \(t\) de l'équation \(x(t)\) et remplacez-le dans \(y(t)\).
6. Mettez \(h=0\) dans l'équation de la trajectoire et résolvez \(y(x_p) = 0\).
8. La flèche est le point le plus haut de la trajectoire. La vitesse verticale s'annule à cet instant précis.
Afficher le corrigé
Corrigé non disponible pour le moment.
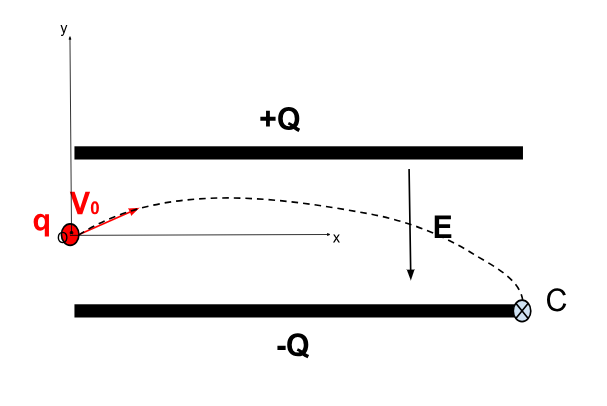
Exercice 2 (Impact d'une charge sur un écran) ❤️ 🌶️ 🌶️ 🌶️
On considère un condensateur dont l'armature supérieure a une charge \(+Q>0\) et l'armature inférieure a une charge \(-Q<0\). On note \(q\) la charge de la particule en entrée du condensateur animée d'une vitesse initiale \(V_0\) selon l'horizontale. Le but de l'exercice est de déterminer les coordonnées du point d'impact \(C\) situé sur l'écran en sortie du condensateur. On suppose que le champ électrique est uniforme.
1. D'après la configuration du condensateur, en déduire le signe de la charge \(q\).
2. En supposant que la particule chargée ne subit pas l'effet de son poids, montrer que les équations horaires du mouvement s'écrivent : \[ x(t)= V_0t \quad \textrm{et} \quad y(t)=-\frac{qE}{2m}t^2 \]
3. Écrire l'équation de la trajectoire de la particule dans le condensateur.
4. Comment appelle-t-on la trajectoire de la particule dans le condensateur ?
5. En supposant que le condensateur mesure en longueur \(d\), déterminer les coordonnées du point au moment où la particule quitte le condensateur.
6. Justifier qu'en sortie du condensateur, la charge a un mouvement rectiligne uniforme.
7. Si l'on note \(\beta\), l'angle de déviation en sortie du condensateur (l'écart angulaire entre l'horizontale et la trajectoire de la particule), montrer que : \[ \tan(\beta)=\frac{V_y}{V_x} \]
8. Montrer que le temps mis par la particule pour traverser la condensateur vaut : \[ t_p=\frac{D}{V_0} \] (Note : il y a une incohérence entre \(d\) (longueur Q5) et \(D\) (temps Q8). On supposera que la longueur est \(d\).)
9. En déduire alors l'expression de la déviation : \[ \beta=-\arctan\left(\frac{qEd}{mV_0^2}\right) \] (Indication : la fonction \(\arctan\) est impaire sur \(\mathbb{R}\))
10. Si l'on note \(D\) la distance entre l'origine du repère et l'écran et \(h_c\) l'ordonnée du point \(C\), montrer que : \[ h_c=(D-d)\tan(\beta) \] (Note : Le schéma montre que la particule a déjà une déviation \(y_S\) à la sortie du condensateur. La formule semble incomplète.)
11. En déduire alors que : \[ h_c=\frac{qEd(d-D)}{mV_0^2} \] (Note : Incohérence de signe probable avec Q9 et Q10)
Voir l'indice
1. La plaque \(+Q\) est en haut, \(-Q\) en bas. Le champ \(\vec{E}\) est dirigé de haut en bas (du \(+\) vers le \(-\)). La particule est déviée vers le haut. Quelle doit être le signe de \(q\) pour que la force \(\vec{F} = q\vec{E}\) soit dirigée vers le haut ?
2. PFD : \(m\vec{a} = q\vec{E}\). Projetez sur les axes \((O,x,y)\) et intégrez deux fois avec les conditions initiales (\(v_x(0)=V_0\), \(v_y(0)=0\), \(x(0)=0\), \(y(0)=0\)).
6. En sortie de condensateur, on suppose \(\vec{E} = \vec{0}\). Quelle est la force résultante ? Appliquez la 1ère loi de Newton.
7. Le vecteur vitesse \(\vec{v}\) est toujours tangent à la trajectoire. Son angle \(\beta\) est donc tel que \(\tan(\beta)\) est la pente de cette tangente, qui est \(\frac{v_y}{v_x}\).
Afficher le corrigé
Corrigé non disponible pour le moment.
Exercice n°3 (Goutte d'eau en chute libre) 🌶️ 🌶️ 🌶️
On considère une goutte d'eau sphérique de rayon \(a\) indéformable de masse volumique \(\rho_e\) qui tombe en chute libre dans un champ de pesanteur constant de norme \(g\).
Lors de sa chute, la goutte d'eau subit une force de traînée constante notée \(\vec{F}_t\) est égale à : \[ \vec{F}_t=-6\pi\eta \frac{a^2}{a+l}\cdot \vec{v} \]
1. Exprimer dans le système international des unités, l'unité de la constante \(\eta\).
2. En négligeant d'abord la poussée d'Archimède, démontrer que la vitesse est solution de l'équation : \[ \frac{d\vec{v}}{dt}+ \frac{9\eta}{2a\rho_e(a+l)}\cdot \vec{v}= \vec{g} \] (Corrigé pour l'homogénéité)
3. Déterminer, à partir de l'équation obtenue, la vitesse maximale atteignable par la goutte d'eau, notée \(v_\infty\).
4. Résoudre l'équation différentielle sachant que la goutte d'eau tombe sans vitesse initiale.
On note \(\rho_a\) la masse volumique de l'air.
5. Démontrer que si l'on considère l'action de la poussée d'Archimède alors l'équation devient : \[ \frac{d\vec{v}}{dt}+ \frac{9\eta}{2a\rho_e(a+l)}\cdot \vec{v}=\left(1-\frac{\rho_a}{\rho_e}\right)\vec{g} \] (Corrigé pour l'homogénéité et le signe)
6. Expliquer pourquoi l'effet de la poussée d'Archimède est négligeable sachant que \(\rho_a=1\) g.L⁻¹.
Voir l'indice
1. Faites une analyse dimensionnelle. Isolez \(\eta\) et exprimez son unité en fonction des autres (Force en N, longueurs en m, vitesse en m/s).
2. Appliquez la 2ème loi de Newton : \(m\vec{a} = \sum \vec{F}\). Les forces sont le Poids (\(m\vec{g}\)) et la force de traînée (\(\vec{F}_t\)). Exprimez la masse \(m\) en fonction de \(\rho_e\) et du volume de la sphère \(V = \frac{4}{3}\pi a^3\).
3. La vitesse limite \(v_\infty\) est atteinte lorsque l'accélération est nulle, c'est-à-dire \(\frac{d\vec{v}}{dt} = \vec{0}\).
5. Ajoutez la Poussée d'Archimède \(\vec{\Pi} = - \rho_a V \vec{g}\) au bilan des forces de la Q2.
6. Comparez \(\rho_a\) à \(\rho_e\) (la masse volumique de l'eau est \(\approx 1000\) g/L).
Afficher le corrigé
Corrigé non disponible pour le moment.
En route vers le supérieur
Exercice n°4 (Vitesse initiale paramétrée) 🌶️ 🌶️ 🌶️
On considère un condensateur dont l'armature supérieure a une charge \(+Q>0\) et l'armature inférieure a une charge \(-Q<0\). On note \(q\) la charge de la particule en entrée du condensateur animée d'une vitesse initiale \(V_0\) selon l'horizontale. Le but de l'exercice est de choisir la bonne vitesse initiale requise pour que la charge se retrouve au point C en sortie du condensateur.
1. Quelle est le signe de la charge \(q\) ?
2. Déterminer les équations horaires du mouvement de la charge \(q\).
On souhaite qu'en sortie d'une condensateur, la charge \(q\) se retrouve au point \(C\) en sortie du condensateur.
3. Écrire l'équation de la trajectoire. La qualifier.
4. Sachant que la particule est lancée au milieu du condensateur, d'écart \(d\) entre ses armatures, justifier que la condition que la charge de retrouve en \(C\) s'écrit : \[ y(D)=-\frac{d}{2} \]
5. En déduire la vitesse initiale requise \(V_0^{req}\) pour que la charge se retrouve en \(C\).
Voir l'indice
1. La plaque \(+Q\) est en haut, \(-Q\) en bas. Le champ \(\vec{E}\) est dirigé de haut en bas (du \(+\) vers le \(-\)). La particule est déviée vers le bas. Quelle doit être le signe de \(q\) pour que la force \(\vec{F} = q\vec{E}\) soit dirigée vers le bas ?
2/3. C'est la même situation que l'exercice 2, mais avec un signe différent pour la force. Reprenez le PFD et les intégrations.
4/5. Prenez votre équation de trajectoire \(y(x)\) de la Q3. Remplacez \(x\) par \(D\) et \(y\) par \(-d/2\). La seule inconnue restante sera \(V_0\). Isolez-la.
Afficher le corrigé
Corrigé non disponible pour le moment.
Exercice n°5 (Condensateurs en série) 🌶️ 🌶️ 🌶️
On décide de coller en série, \(2N\) condensateurs, \(N\) condensateurs dont l'armature supérieure est chargée positive \(+Q>0\), l'autre négative chargée \(-Q<0\) et \(N\) condensateurs dont l'armature supérieure est chargée négative \(-Q<0\), l'autre positive chargée \(+Q>0\) répartis de façon alternée.
1. Schématiser la situation.
On considère une particule de charge \(q>0\) qu'on éjecte avec une vitesse \(V_0\) suivant l'horizontale à l'entrée du premier condensateur (armature supérieur positive, armature inférieure négative).
2. En supposant que la trajectoire de la charge ne rencontre jamais les armatures des condensateurs (la charge reste confinée dans les condensateurs), dessiner la trajectoire de la charge dans le cas où \(2N=4\).
3. Dans un cas simplifié, déterminer l'équation de la trajectoire de la charge \(q\) à travers les condensateurs pour \(2N=2\). (un condensateur avec les armatures supérieure positive et inférieure négative, un second condensateur avec les armatures supérieure négative et inférieure positive).
Voir l'indice
1. Dessinez 4 condensateurs à la suite : `[+ -] [- +] [+ -] [- +]`.
2. La charge \(q>0\) entre dans le premier champ \(\vec{E}_1\) (vers le bas). Elle subit \(\vec{F}_1 = q\vec{E}_1\) (vers le bas) -> trajectoire parabolique vers le bas. Puis elle entre dans le deuxième champ \(\vec{E}_2\) (vers le haut). Elle subit \(\vec{F}_2 = q\vec{E}_2\) (vers le haut) -> trajectoire parabolique vers le haut. Répétez.
3. C'est un problème "par morceaux". Trouvez l'équation \(y_1(x)\) pour \(0 < x < L_1\) (1er condensateur). Calculez la position \(y_1(L_1)\) et la vitesse \(\vec{v}_1(L_1)\) en sortie. Utilisez-les comme conditions initiales pour trouver la *nouvelle* équation de trajectoire \(y_2(x)\) dans le 2ème condensateur.
Afficher le corrigé
Corrigé non disponible pour le moment.