Terminale : Matrices et application aux graphes
📚 Table des matières
- 1. Introduction aux Matrices
- 2. Opérations sur les matrices
- 3. Introduction aux Graphes
- 4. Matrice d'adjacence d'un graphe
- 5. Puissances de la matrice d'adjacence
- 6. Matrices et systèmes linéaires
- 7. Suites récurrentes linéaires
- 8. Introduction aux chaînes de Markov
- 9. Graphe orienté pondéré d'une chaîne de Markov
- 10. Évolution d'une chaîne de Markov
- 11. Distributions invariantes
- 12. Exemple complet : Modèle météorologique
1. Introduction aux Matrices
Les matrices sont des objets mathématiques fondamentaux qui permettent de représenter et de résoudre de nombreux problèmes issus de diverses disciplines. Elles constituent un outil puissant pour modéliser des situations complexes et effectuer des calculs de manière efficace.
Historiquement, l'utilisation de tableaux de nombres pour résoudre des systèmes linéaires remonte à l'Antiquité, mais c'est Arthur Cayley qui, au milieu du XIXe siècle, a formalisé la notion de matrice comme objet de calcul représentant des transformations linéaires.
Définition 1.
Une matrice est un tableau rectangulaire de nombres réels disposés en lignes et en colonnes. Une matrice à \(m\) lignes et \(n\) colonnes est appelée matrice de format \((m,n)\) ou matrice \(m \times n\).
On note généralement une matrice par une lettre majuscule : \(A = (a_{i,j})\) où \(a_{i,j}\) désigne l'élément situé à la ligne \(i\) et à la colonne \(j\).
Exemple
La matrice \(A = \begin{pmatrix} 2 & -1 & 3 \\ 0 & 5 & -2 \end{pmatrix}\) est une matrice \(2 \times 3\). On a \(a_{1,2} = -1\) et \(a_{2,3} = -2\).
Définition 2.
On distingue plusieurs types particuliers de matrices :
1. Une matrice carrée d'ordre \(n\) est une matrice de format \((n,n)\)
2. Une matrice ligne est une matrice de format \((1,n)\)
3. Une matrice colonne est une matrice de format \((m,1)\)
4. La matrice identité d'ordre \(n\), notée \(I_n\), est la matrice carrée dont les éléments diagonaux valent 1 et les autres valent 0
2. Opérations sur les matrices
Pour manipuler efficacement les matrices, il est essentiel de maîtriser les opérations de base. Ces opérations respectent des règles précises qui permettent de structurer le calcul matriciel.
2.1. Addition et multiplication par un scalaire
Proposition 1.
Soient \(A\) et \(B\) deux matrices de même format \((m,n)\) et \(k\) un nombre réel.
1. L'addition \(A + B\) est la matrice de format \((m,n)\) dont l'élément \((i,j)\) est \(a_{i,j} + b_{i,j}\)
2. La multiplication par un scalaire \(kA\) est la matrice de format \((m,n)\) dont l'élément \((i,j)\) est \(k \cdot a_{i,j}\)
2.2. Multiplication de matrices
La multiplication de matrices est une opération plus complexe mais fondamentale. Elle permet de composer des transformations et de résoudre des systèmes d'équations.
Proposition 2.
Soient \(A\) une matrice de format \((m,p)\) et \(B\) une matrice de format \((p,n)\). Le produit \(AB\) est la matrice de format \((m,n)\) dont l'élément \((i,j)\) est :
Remarque importante. Pour que le produit \(AB\) soit défini, il est nécessaire que le nombre de colonnes de \(A\) soit égal au nombre de lignes de \(B\). De plus, la multiplication matricielle n'est généralement pas commutative : \(AB \neq BA\) en général.
Exemple
Calculons le produit \(\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix}\) :
2.3. Inverse d'une matrice carrée
L'inverse d'une matrice est un concept crucial qui généralise la notion d'inverse d'un nombre réel au contexte matriciel.
Définition 3.
Soit \(A\) une matrice carrée d'ordre \(n\). On dit que \(A\) est inversible s'il existe une matrice \(B\) d'ordre \(n\) telle que \(AB = BA = I_n\). La matrice \(B\) est alors unique et est appelée inverse de \(A\), notée \(A^{-1}\).
Proposition 3.
Pour une matrice carrée d'ordre 2 : \(A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}\)
Si \(ad - bc \neq 0\), alors \(A\) possède un inverse donné par :
Remarque hors-programme : La condition \(ad - bc \neq 0\) est à retenir comme une condition pratique de calcul. Plus tard, cette notion sera définie comme le déterminant d'une matrice.
2.4. Puissances d'une matrice carrée
Les puissances de matrices sont particulièrement utiles pour étudier l'évolution de systèmes dynamiques.
Définition 4.
Soit \(A\) une matrice carrée d'ordre \(n\) et \(k\) un entier naturel non nul. On définit :
1. \(A^0 = I_n\) (par convention)
2. \(A^1 = A\)
3. \(A^k = A \times A^{k-1}\) pour \(k \geq 2\)
3. Introduction aux Graphes
Les graphes constituent un outil fondamental des mathématiques discrètes. Ils permettent de modéliser de nombreuses situations où des objets sont reliés entre eux par des relations.
L'histoire des graphes remonte au moins à Euler avec le célèbre problème des ponts de Königsberg en 1736. Aujourd'hui, les graphes trouvent des applications dans de nombreux domaines : réseaux sociaux, transport, informatique, biologie, etc.
Définition 5.
Un graphe \(G\) est un ensemble fini de sommets (ou nœuds) reliés par des arêtes. On note \(G = (S, A)\) où \(S\) est l'ensemble des sommets et \(A\) l'ensemble des arêtes.
Exemple
Considérons un réseau social simplifié où les sommets représentent des personnes et les arêtes des relations d'amitié. Si Alice, Bob, Charlie et Diana sont amis selon le schéma : Alice-Bob, Bob-Charlie, Charlie-Diana, Alice-Charlie, alors nous obtenons un graphe à 4 sommets et 4 arêtes :
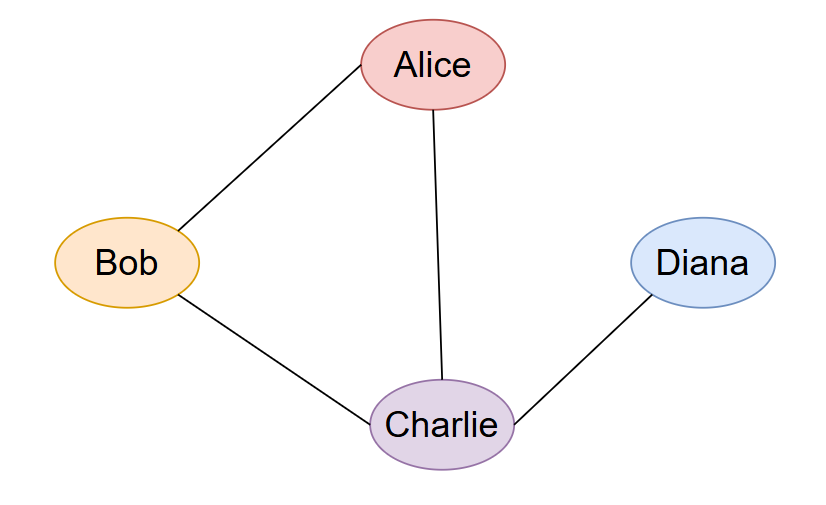
Figure 1. Représentation du graphe
Définition 6.
Dans un graphe :
1. Deux sommets sont adjacents s'ils sont reliés par une arête
2. Le degré d'un sommet est le nombre d'arêtes qui lui sont incidentes
3. L'ordre d'un graphe est son nombre de sommets
4. Une chaîne est une suite d'arêtes consécutives reliant deux sommets
5. La longueur d'une chaîne est le nombre d'arêtes qui la composent
6. Un graphe est connexe si tout couple de sommets peut être relié par une chaîne
Définition 7.
Un graphe complet d'ordre \(n\), noté \(K_n\), est un graphe où chaque sommet est adjacent à tous les autres sommets. Il possède donc \(\frac{n(n-1)}{2}\) arêtes.
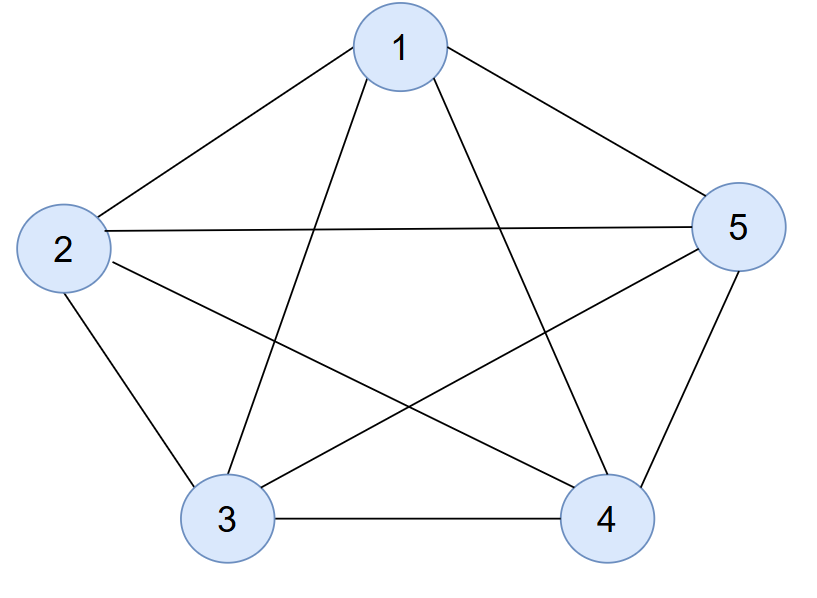
Figure 2. Représentation d'un graphe complet d'ordre 5
4. Matrice d'adjacence d'un graphe
L'un des liens les plus importants entre matrices et graphes est la représentation matricielle d'un graphe par sa matrice d'adjacence. Cette représentation permet d'appliquer les outils du calcul matriciel à l'étude des graphes.
Définition 8.
Soit \(G\) un graphe d'ordre \(n\) dont les sommets sont numérotés de 1 à \(n\). La matrice d'adjacence de \(G\) est la matrice carrée \(M\) d'ordre \(n\) définie par :
Propriétés importantes de la matrice d'adjacence :
1. Les éléments de la diagonale sont nuls
2. La somme des éléments de la ligne \(i\) (ou de la colonne \(i\)) donne le degré du sommet \(i\)
Exemple
Pour un graphe complet \(K_3\) avec sommets \(\{1, 2, 3\}\) et arêtes \(\{1-2, 2-3, 1-3\}\), graphiquement :
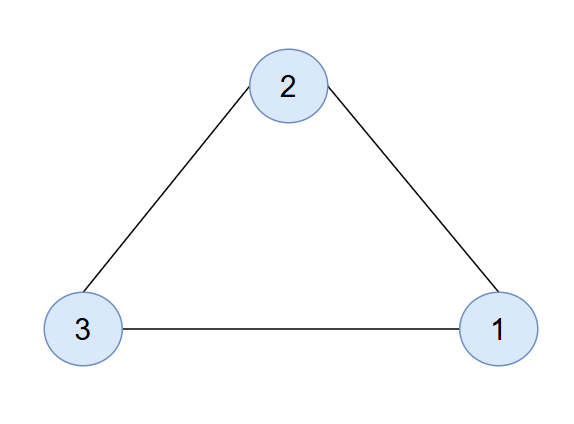
Figure 3. Représentation d'un graphe complet d'ordre 3
la matrice d'adjacence est :
5. Puissances de la matrice d'adjacence
Les puissances de la matrice d'adjacence révèlent des informations remarquables sur la structure du graphe, notamment sur le nombre de chemins entre les sommets.
Théorème 1.
Soit \(G\) un graphe de matrice d'adjacence \(M\). Pour tout entier naturel \(n \geq 1\), l'élément \((i,j)\) de la matrice \(M^n\) donne le nombre de chaînes de longueur exactement \(n\) reliant le sommet \(i\) au sommet \(j\).
Preuve
Démonstration. Nous procédons par récurrence sur \(n\).
Cas de base : Pour \(n = 1\), \(M^1 = M\). Par définition de la matrice d'adjacence, \(M_{i,j} = 1\) s'il existe une arête entre \(i\) et \(j\) (donc une chaîne de longueur 1), et \(M_{i,j} = 0\) sinon. Le résultat est donc vrai pour \(n = 1\).
Hérédité : Supposons le résultat vrai pour un entier \(n \geq 1\). Montrons qu'il est vrai pour \(n + 1\).
L'élément \((i,j)\) de \(M^{n+1} = M^n \times M\) est : \[ (M^{n+1})_{i,j} = \sum_{k=1}^{p} (M^n)_{i,k} \times M_{k,j} \]
Par hypothèse de récurrence, \((M^n)_{i,k}\) compte les chaînes de longueur \(n\) de \(i\) à \(k\), et \(M_{k,j}\) vaut 1 s'il y a une arête de \(k\) à \(j\), 0 sinon.
Ainsi, \((M^n)_{i,k} \cdot M_{k,j}\) compte les chaînes de longueur \(n+1\) de \(i\) à \(j\) passant par \(k\). En sommant sur tous les sommets intermédiaires \(k\), on obtient le nombre total de chaînes de longueur \(n+1\) de \(i\) à \(j\).
Application
Reprenons l'exemple du triangle \(K_3\). Calculons \(M^2\) :
Cela signifie qu'il y a 2 chaînes de longueur 2 entre chaque sommet et lui-même (par exemple, de 1 à 1 : \(1 \to 2 \to 1\) et \(1 \to 3 \to 1\)), et 1 chaîne de longueur 2 entre chaque paire de sommets distincts.
6. Matrices et systèmes linéaires
Les matrices constituent un outil puissant pour représenter et résoudre des systèmes d'équations linéaires. Cette application est fondamentale en mathématiques et trouve de nombreuses utilisations pratiques.
Définition 9.
Un système de \(m\) équations linéaires à \(n\) inconnues peut s'écrire sous forme matricielle : \[ AX = B \] où \(A\) est la matrice des coefficients (format \(m \times n\)), \(X\) est la matrice colonne des inconnues (format \(n \times 1\)), et \(B\) est la matrice colonne des seconds membres (format \(m \times 1\)).
Proposition 4.
Si \(A\) est une matrice carrée inversible, alors le système \(AX = B\) admet une unique solution donnée par : \[ X = A^{-1}B \]
7. Suites récurrentes linéaires
Les matrices permettent également d'étudier efficacement les suites récurrentes linéaires, particulièrement utiles en modélisation.
Définition 10.
Une suite de matrices colonnes \((U_n)\) vérifiant une relation de récurrence du type : \[ U_{n+1} = AU_n + C \] où \(A\) est une matrice carrée et \(C\) une matrice colonne constante, peut être étudiée à l'aide du calcul matriciel.
Proposition 5.
Si \(A\) est inversible et si \(V\) est un point fixe de la récurrence (c'est-à-dire \(V = AV + C\)), alors : \[ U_n = A^n(U_0 - V) + V \] où \(V = (I - A)^{-1}C\) (quand \(I - A\) est inversible).
8. Introduction aux chaînes de Markov
Les chaînes de Markov constituent une application remarquable des matrices aux probabilités. Elles modélisent des processus aléatoires où l'état futur ne dépend que de l'état présent.
Définition 11.
Une chaîne de Markov à \(n\) états est un processus aléatoire où :
1. À chaque étape, le système se trouve dans l'un des \(n\) états possibles
2. La probabilité de passer d'un état à un autre ne dépend que de l'état actuel (propriété de Markov)
3. Ces probabilités de transition sont constantes dans le temps
Définition 12.
La matrice de transition \(P\) d'une chaîne de Markov à \(n\) états est la matrice carrée d'ordre \(n\) où \(P_{i,j}\) représente la probabilité de passer de l'état \(i\) à l'état \(j\) en une étape.
Propriétés de la matrice de transition :
1. Tous les éléments sont positifs ou nuls : \(P_{i,j} \geq 0\)
2. La somme de chaque ligne vaut 1 : \(\sum_{j=1}^{n} P_{i,j} = 1\)
Exemple
Un élève peut choisir chaque jour de venir au lycée soit en bus (B), soit en vélo (V).
On observe les habitudes suivantes :
1. Si aujourd'hui il vient en bus, il y a 70% de chances qu'il vienne encore en bus le lendemain, et 30% de chances qu'il vienne en vélo.
2. Si aujourd'hui il vient en vélo, il y a 50% de chances qu'il vienne en bus le lendemain, et 50% de chances qu'il vienne encore en vélo.
On peut modéliser cette situation par la matrice de transition suivante : \[ P = \begin{pmatrix} 0.7 & 0.3 \\ 0.5 & 0.5 \\ \end{pmatrix} \] où la première ligne correspond à l'état bus (B), la seconde à l'état vélo (V).
On peut lire les coefficients de la matrice comme suit :
1. \(P_{1,1} = 0.7\) : Si aujourd'hui il vient en bus, il y a 70% de chances qu'il revienne en bus demain.
2. \(P_{1,2} = 0.3\) : Si aujourd'hui il vient en bus, il y a 30% de chances qu'il prenne le vélo demain.
3. \(P_{2,1} = 0.5\) : Si aujourd'hui il vient en vélo, il y a 50% de chances qu'il prenne le bus demain.
4. \(P_{2,2} = 0.5\) : Si aujourd'hui il vient en vélo, il y a 50% de chances qu'il revienne en vélo demain.
On peut utiliser cette chaîne de Markov pour prévoir le mode de transport de l’élève les jours suivants à partir de son choix actuel.
9. Graphe orienté pondéré d'une chaîne de Markov
Une chaîne de Markov peut être représentée visuellement par un graphe orienté pondéré, facilitant ainsi la compréhension du processus.
Définition 13.
Le graphe orienté pondéré associé à une chaîne de Markov est un graphe où :
1. Chaque sommet représente un état de la chaîne
2. Il y a une arête orientée de l'état \(i\) vers l'état \(j\) si \(P_{i,j} > 0\)
3. Cette arête est pondérée par la probabilité \(P_{i,j}\)
Exemple
Considérons la chaîne de Markov suivante avec deux états \(A\) et \(B\) et la matrice de transition : \[ P = \begin{pmatrix} 0.7 & 0.3 \\ 0.4 & 0.6 \\ \end{pmatrix} \]
Le graphe orienté pondéré associé s’écrit alors :
Concrètement, cela signifie que :
1. Depuis \(A\), on reste sur \(A\) avec probabilité \(0.7\) et on passe à \(B\) avec probabilité \(0.3\).
2. Depuis \(B\), on reste sur \(B\) avec probabilité \(0.6\) et on passe à \(A\) avec probabilité \(0.4\).
10. Évolution d'une chaîne de Markov
L'évolution temporelle d'une chaîne de Markov s'exprime élégamment à l'aide des puissances de la matrice de transition.
Définition 14.
La distribution initiale d'une chaîne de Markov est représentée par une matrice ligne \(\pi_0 = (\pi_0^{(1)}, \pi_0^{(2)}, \ldots, \pi_0^{(n)})\) où \(\pi_0^{(i)}\) est la probabilité que le système soit initialement dans l'état \(i\).
Théorème 2.
Pour une chaîne de Markov de matrice de transition \(P\) :
1. L'élément \((i,j)\) de \(P^n\) donne la probabilité de passer de l'état \(i\) à l'état \(j\) en exactement \(n\) transitions
2. La distribution après \(n\) transitions est donnée par : \(\pi_n = \pi_0 P^n\)
Exemple
Un animal peut se trouver dans l’un des trois habitats suivants : forêt (F), prairie (P) ou rivière (R).
À chaque jour, il peut changer d’habitat selon la matrice de transition suivante :
\[ P = \begin{pmatrix} 0.6 & 0.3 & 0.1 \\ 0.2 & 0.7 & 0.1 \\ 0.3 & 0.3 & 0.4 \\ \end{pmatrix} \]
où la première ligne correspond à la forêt, la deuxième à la prairie, la troisième à la rivière.
Par exemple, \(P_{1,2} = 0.3\) signifie que si l’animal est en forêt, il a 30\% de chances d’aller en prairie le lendemain.
Distribution initiale : Supposons que l’animal commence en forêt avec certitude, donc \(\pi_0 = (1\;\;0\;\;0)\).
Distribution après un jour : \[ \pi_1 = \pi_0 P = (1\;\;0\;\;0) \begin{pmatrix} 0.6 & 0.3 & 0.1 \\ 0.2 & 0.7 & 0.1 \\ 0.3 & 0.3 & 0.4 \\ \end{pmatrix} = (0.6\;\;0.3\;\;0.1) \]
Interprétation :
Après un jour, l’animal a 60\% de chances d’être encore en forêt, 30\% d’être en prairie et 10\% d’être à la rivière.
11. Distributions invariantes
Un concept fondamental des chaînes de Markov est celui de distribution invariante, qui décrit le comportement asymptotique du système.
Définition 15.
Une distribution invariante (ou stationnaire) d'une chaîne de Markov de matrice \(P\) est une matrice ligne \(\pi\) telle que : \[ \pi = \pi P \] Autrement dit, si le système atteint cette distribution, il y reste indéfiniment.
12. Exemple complet : Modèle météorologique
Considérons un modèle météorologique simplifié à deux états : "Beau" (B) et "Pluvieux" (P).
Supposons que :
1. S'il fait beau aujourd'hui, il y a 70% de chances qu'il fasse beau demain et 30% qu'il pleuve
2. S'il pleut aujourd'hui, il y a 40% de chances qu'il fasse beau demain et 60% qu'il pleuve
La matrice de transition est : \[ P = \begin{pmatrix} 0.7 & 0.3 \\ 0.4 & 0.6 \end{pmatrix} \]
Pour trouver la distribution invariante \(\pi = (\pi_B, \pi_P)\), résolvons : \[ (\pi_B, \pi_P) \begin{pmatrix} 0.7 & 0.3 \\ 0.4 & 0.6 \end{pmatrix} = (\pi_B, \pi_P) \]
Cela donne le système : \[ \begin{cases} 0.7\pi_B + 0.4\pi_P = \pi_B \\ 0.3\pi_B + 0.6\pi_P = \pi_P \\ \pi_B + \pi_P = 1 \end{cases} \]
En résolvant, on trouve \(\pi_B = \frac{4}{7}\) et \(\pi_P = \frac{3}{7}\).
À long terme, il fera beau environ 57% du temps et il pleuvra environ 43% du temps.