Terminale : Limites de fonctions
Dans tout ce chapitre, on définit \(I\) comme un intervalle de \(\mathbb{R}\). Soit \(f : \mathbb{R} \to \mathbb{R}\) une fonction.
📚 Table des matières
1. Limites en l'infini
1.1. Limite finie en l'infini
Intuitivement, dire qu'une fonction \(f\) tend vers un certain réel \(l\) en l'infini signifie que l'on pourra toujours trouver \(f(x)\) aussi proche que l'on veut de \(l\), en s'assurant de \(x\) soit suffisamment grand (par exemple, plus grand qu'un certain réel \(A\)). Graphiquement, cela signifie que si l'on veut que \(f(x)\) soit dans l'intervalle rouge (et on peut le choisir de n'importe quelle largeur), il suffit de choisir \(x\) dans l'intervalle vert:
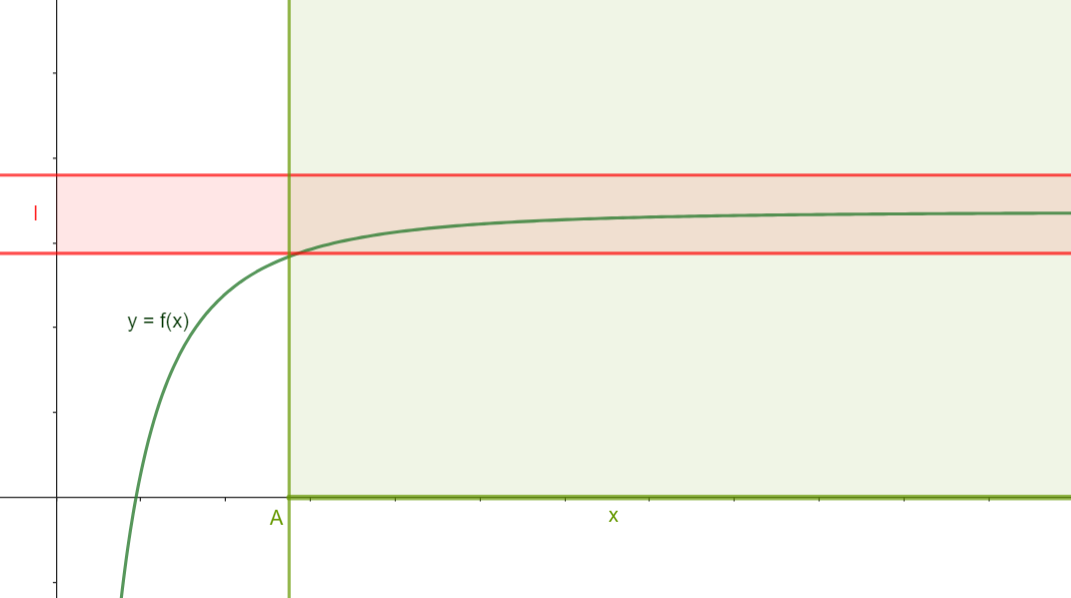
Figure 1. Représentation de limite finie en l'infini
Définition 1. (Limite en \(+\infty\))
\(f\) admet une limite \(l\) en \(+\infty\) si tout intervalle ouvert contenant \(l\) contient \(f(x)\) à partir d'une valeur suffisamment grande de \(x\). On note alors :
La droite d'équation \(y=l\) est appelée asymptote horizontale à la courbe de \(f\).
1.2. Limite infini en l'infini
Cette fois, en raisonnant comme le cas précédent, dire qu'une fonction tend vers \(+\infty\) en \(+\infty\), cela revient à dire que \(f(x)\) peut être aussi grand que l'on veut, autant que l'on choisisse \(x\) suffisamment grand :
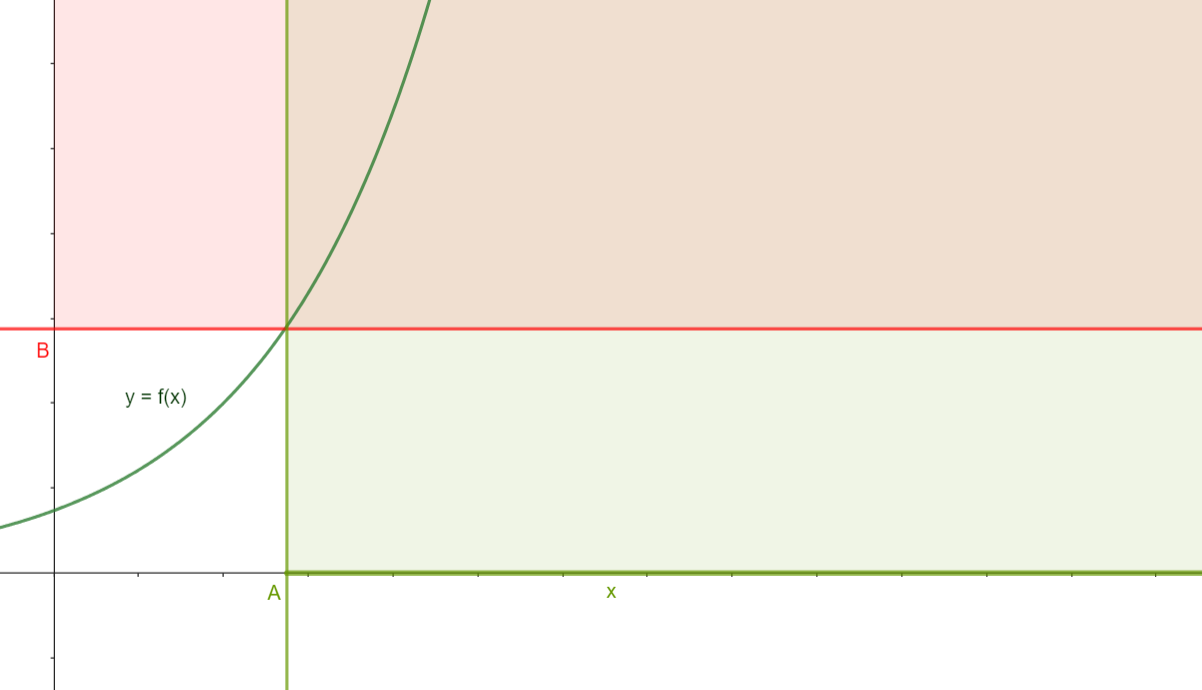
Figure 2. Représentation de limite infinie en l'infini
Comme précédemment, on en déduit la définition associée :
Définition 2. (Limite en \(+\infty\))
\(f\) tend vers \(+\infty\) en \(+\infty\) si tout intervalle de la forme \(]a,+\infty[\) contient \(f(x)\) à partir d'une valeur suffisamment grande de \(x\). On note alors :
Dans les deux cas, l'énoncé des limites en \(-\infty\) est analogue.
1.3. Autres cas
Attention, une fonction \(f\) ne possède pas forcément une limite en \(\pm \infty\), il suffit de considérer le graphe suivant :
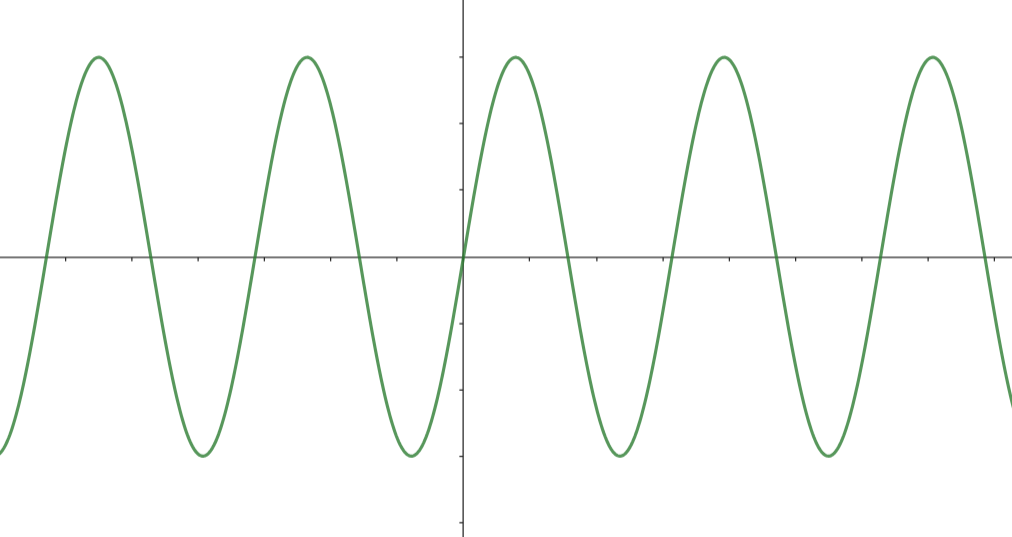
Figure 3. Cas d'une fonction sans limite
1.4. Quelques exemples importants en \(+\infty\)
Dans cette sous-section, nous allons détailler quelques limites aux infinies à connaître.
1.4.1. Puissance de \(x\)
Regardons dans un premier temps le graphe de la fonction \(x \mapsto x^2\) :
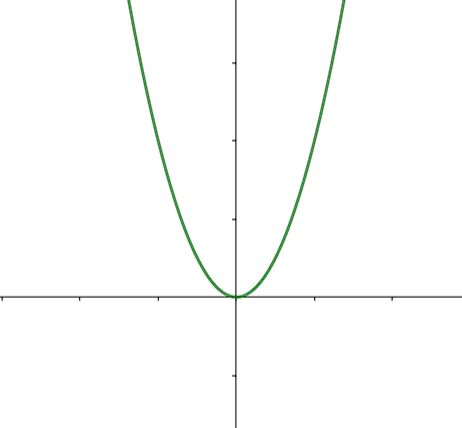
Figure 4. Représentation graphique de la fonction carrée
Ici, on remarque que :
On en déduit une généralisation :
Propriété 1.
Pour tout \(k \in \mathbb{N}\) supérieur à 1, la fonction \(x \mapsto x^k\) tend vers \(+\infty\) en \(+\infty\), autrement dit:
Pour le cas en \(-\infty\), on se contente d'énoncer les limites pour les fonctions carrée et cube :
Propriété 2. (Limites de la fonction \(x \mapsto x^2\))
Propriété 3. (Limites de la fonction \(x \mapsto x^3\))
1.4.2. Racine carrée
Le résultat de la propriété 1 est encore vrai pour la fonction racine carrée \(x \mapsto \sqrt{x}\) :
Propriété 4.
Ici, cela n'a pas de sens de parler de sa limite en \(-\infty\) puisque la fonction n'est pas définie pour des réels négatifs.
1.5. Fonction inverse
Cette fois, le cas des limites en \(+\infty\) et \(-\infty\) de \(x \mapsto \frac{1}{x}\) fait partie de la section 1.1, et tend vers une valeur finie. En effet :
Propriété 5.
Un simple graphe permet de s'assurer de la véracité de la propriété précédente :
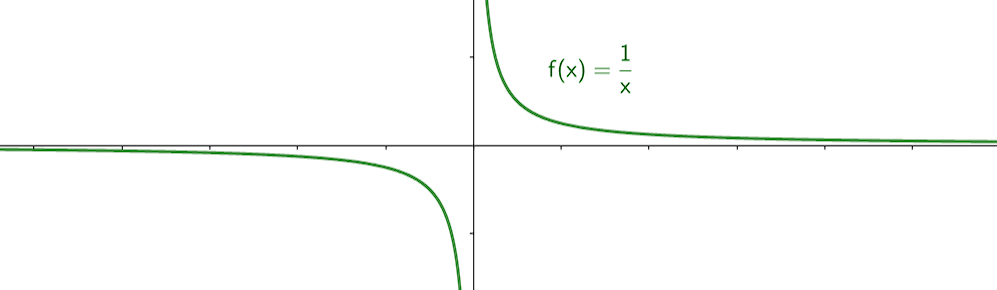
Figure 5. Représentation graphique de la fonction inverse
Néanmoins, dans le cas de la fonction inverse, on pourrait s'intéresser non plus à sa limite aux infinies, mais à sa limite en 0, puisque cette fonction n'est pas définie en ce point. C'est l'objet de la section suivante.
2. Limites en un réel \(a\)
Intuitivement, dire que \(f\) tend vers \(+\infty\) en un certain réel \(a\), c'est dire que l'on peut trouver \(f(x)\) aussi grand que l'on veut, autant que l'on choisisse \(x\) suffisamment proche de \(a\). Pour s'en convaincre, il suffit de prendre l'exemple précédent de la fonction inverse. Pour avoir \(f(x)\) supérieur à un certain réel B, il faut prendre \(x\) dans un intervalle précis I (en vert) :
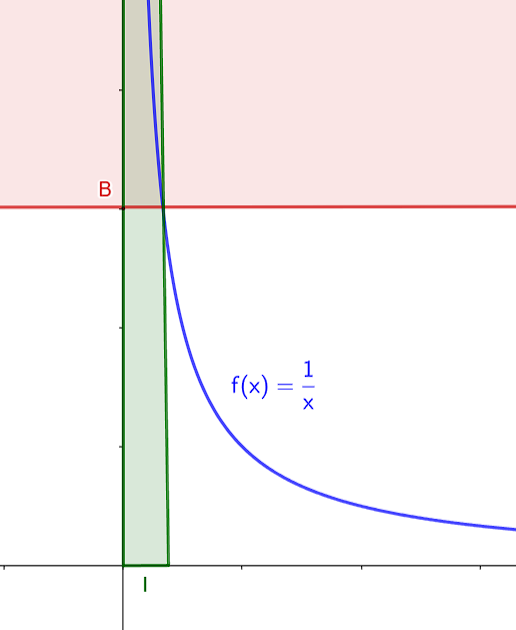
Figure 6. Représentation graphique d'une limite infinie en un point
On ne s'intéressera donc qu'à des limites infinies en un réel \(a\) dans cette section, puisque le cas d'une limite finie est inintéressant (voir chapitre Continuité).
2.1. Limite infinie
On fournit désormais une formalisation du cas précédent :
Définition 3.
La fonction \( f \) a pour limite \( +\infty \) en \( a \) si tout intervalle \( ]M; +\infty[ \) contient toutes les valeurs de \( f(x) \) pour \( x \) assez proche de \( a \). On note alors :
La droite d’équation \( x = a \) est dite asymptote verticale à la courbe représentative de \(f\).
On a une définition analogue pour le cas où la limite vaut \(-\infty\).
Désormais, comme vu dans les chapitres précédents, certaines fonctions sont en réalité des sommes, produit ou quotient d'autres fonctions. Par exemple :
Exemple 1.
La fonction \(x \mapsto x^3 - x^2\) est en réalité la somme de deux fonctions \(x \mapsto f(x) + g(x)\) où :
\[ f : x \mapsto x^3 \]
et :
\[ g : x \mapsto -x^2 \]
Certes, on sait calculer la limite de ces deux fonctions de manière indépendante. Néanmoins, comment calculer la limite de la somme? C'est l'objet de la section suivante.
3. Opérations sur les limites
Pour déterminer la limite dans les différents cas, on utilise à chaque fois un tableau.
3.1. Limite d'une somme
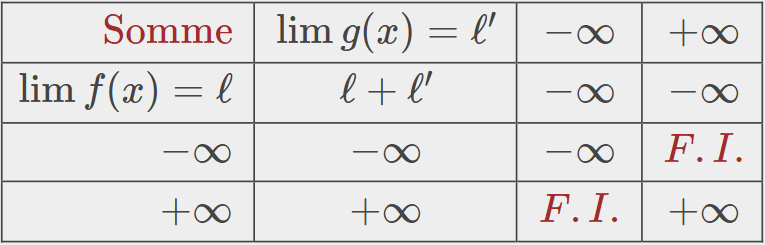
Ici, le sigle f.i. signifie forme indéterminée. Celui-ci ne veut pas dire que la limite de la somme n'existe pas, mais plutôt que l'on ne peut PAS connaître la limite et que cette dernière peut valoir n'importe quoi.
Exemple 2.
Prenons comme exemple pour exhiber une forme indéterminée la fonction \(x \mapsto x^3 - x^2\). Cette fonction est en réalité la somme de \(f : x \mapsto x^3\) et \(g : x \mapsto -x^2\). Or, en \(+ \infty\):
\[ \displaystyle\lim_{x \to +\infty} f(x) = +\infty \text{ ET } \displaystyle\lim_{x \to +\infty} g(x) = - \infty \]
On est donc face à une forme indéterminée. La valeur de la limite ne peut pas être connue avec les résultats pour une somme.
Il nous faut donc encore voir le cas d'un produit et d'un quotient.
3.2. Limite d'un produit
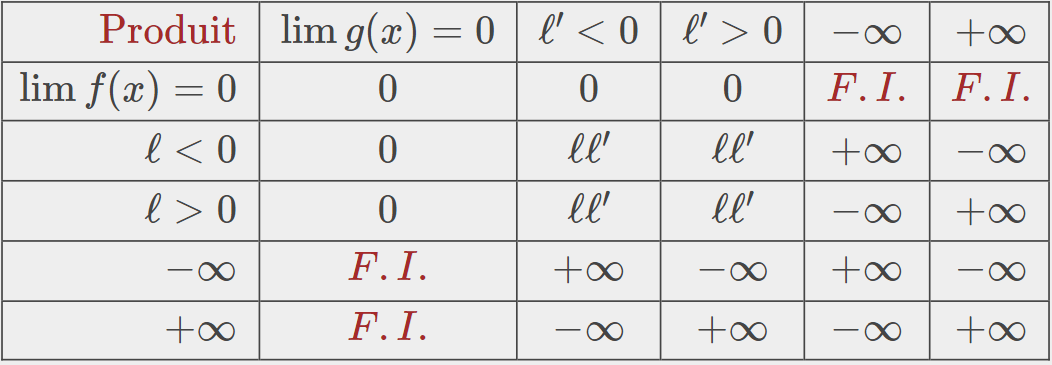
Exemple 2 (bis).
Si on reprend l'exemple 2, en factorisant l'expression pour \(x \in \mathbb{R}\):
\[ x^3-x^2 = x^3 (1 - \frac{1}{x}) \]
Cette fois, en remarquant que sous cette forme, la fonction est le produit de \(x \mapsto x^3\) et \(x \mapsto (1 - \frac{1}{x})\), nous n'avons plus de problème de forme indéterminée. La limite vaut alors :
3.3. Limite d'un quotient
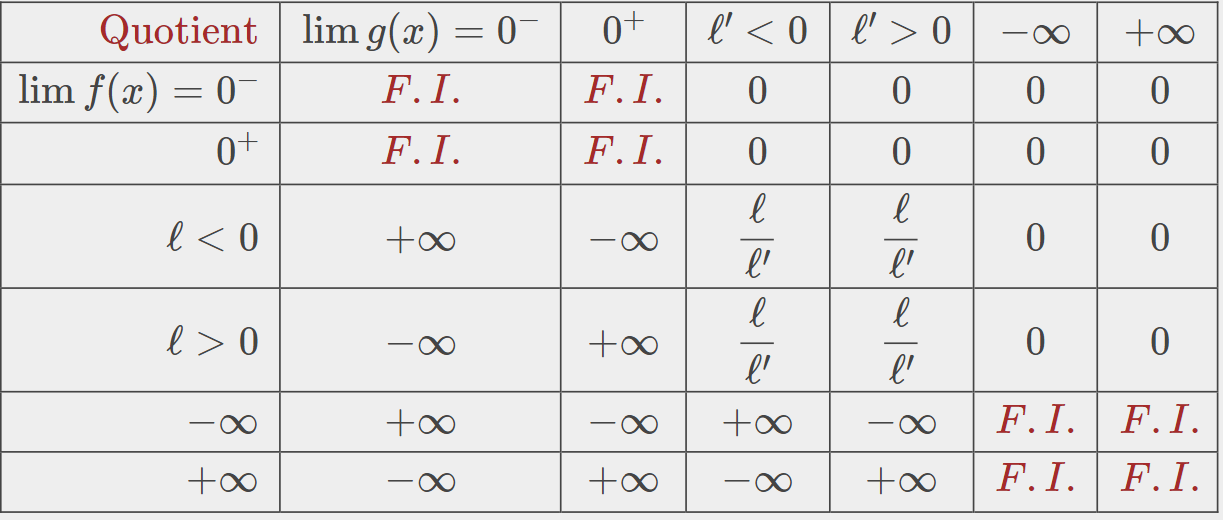
4. Limite d'une fonction composée
Considérons ici deux fonctions f et g et on note respectivement \(D_f\) et \(D_g\) leur domaine de définition de sorte que :
\[ f : D_f \rightarrow D_g \]
\[ g : D_g \rightarrow \mathbb{R} \]
On obtient alors :
\[ x \xrightarrow{\ \ f \ \ } f(x) \xrightarrow{\ \ g \ \ } g(f(x)) \]
Alors :
Propriété 6. (Limite d'une composée)
Si \(\displaystyle\lim_{x \to a} f(x) = b\) et \(\displaystyle\lim_{y \to b} g(y) = c\) alors :
Exemple 3.
Pour bien comprendre ce résultat, prenons une composée de fonctions simples : \(h : x \mapsto e^{-x^2}\). La fonction \(h\) est la composé de la fonction \(f : x \mapsto -x^2\) avec \(g : y \mapsto e^y\). Cherchons à déterminer la limite de \(h\) en \(+\infty\).
On a : \(\displaystyle\lim_{x \to +\infty} f(x) = -\infty\) et donc \(\displaystyle\lim_{y \to -\infty} g(y) = 0\).
D'après le théorème précédent, on en déduit que :
5. Théorèmes de comparaison
Soient \(a\) et \(l\) deux nombres réels. Considérons ici trois fonctions \(f\), \(g\) et \(h\) définies sur \(]a;+\infty[\).
Théorème 1. (Théorème des "Gendarmes")
Si pour tout \(x\) dans l'intervalle \(]a;+\infty[\), on a :
1. \(g(x) \leq f(x) \leq h(x)\)
2. \(\displaystyle\lim_{x \to +\infty} g(x) = \displaystyle\lim_{x \to +\infty} h(x) = l\)
Alors : \(\displaystyle\lim_{x \to +\infty} f(x) = l\)
Théorème 2. (Théorème de comparaison)
Si pour tout \(x\) dans l'intervalle \(]a;+\infty[\), on a :
1. \(g(x) \leq f(x)\)
2. \(\displaystyle\lim_{x \to +\infty} g(x) = +\infty\)
Alors : \(\displaystyle\lim_{x \to +\infty} f(x) = +\infty\)
Les deux théorèmes ont un résultat analogue en \(-\infty\). Par exemple, le théorème 2 devient :
Théorème 2. (Théorème de comparaison version \(-\infty\))
Si pour tout \(x\) dans l'intervalle \(]-\infty;a[\), on a :
1. \(f(x) \leq g(x)\)
2. \(\displaystyle\lim_{x \to +\infty} g(x) = -\infty\)
Alors : \(\displaystyle\lim_{x \to +\infty} f(x) = -\infty\)