Terminale : Calcul intégral
Ce chapitre fait suite au cours sur les primitives. Il introduit un nouveau symbole intégrale noté \(\int\) qui est l'analogie du symbole somme \(\sum\) lorsqu'il y a continuité. Nous verrons que l'intégrale a d'abord un sens géométrique qui peut lui-même s'étendre, grâce au théorème fondamental de l'analyse, à un sens plus calculatoire mettant en jeu la notion de primitive.
📚 Table des matières
1. L'intégrale (au sens géométrique)
Soit \(f\) une fonction continue sur un intervalle \(I\subset\mathbb{R}\). On donne sa représentation graphique sur l'intervalle \([a;b]\subset I\) avec \(a\) et \(b\) deux réels :
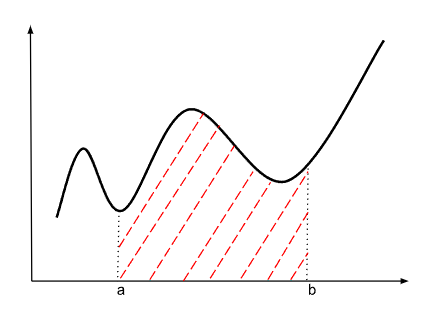
Le domaine hachurée en rouge sur l'intervalle \([a;b]\) correspond à une aire algébrique notée \(\mathcal{A}\) comprise entre la courbe représentative de \(f\), l'axe des abscisses et les droites verticales d'équation \(x=a\) et \(x=b\).
On préfère, pour exprimer \(\mathcal{A}\), introduire la notation \(\int\) en écrivant :
La question à se poser est : quelle est la signification du symbole \(\int\) ? On l'a utilisé ici pour calculer une aire algébrique (elle peut être compter positive ou négative en fonction de la position de la courbe de \(f\) par rapport à l'axe des abscisses) mais on peut la voir comme un symbole \(\sum\).
En effet, si l'on veut calculer géométriquement cette aire \(\mathcal{A}\), on pourrait la découper à l'aide de figures simples dont l'aire est aisément calculable puis tout sommer. C'est l'idée de la naissance du symbole \(\int\) sauf qu'ici, les figures qu'on prend seront si petites qu'il n'y a pas d'imprécision sur le résultat final, il sera exact !
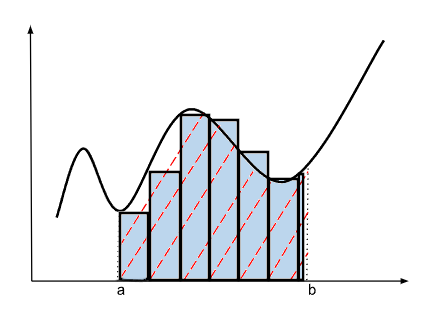
Cette illustration met en évidence la construction de l'intégrale. On partage le domaine hachuré avec des rectangles de largeur très fine qu'on notera \(dx\) et de hauteur égale à \(f(x)\) qui nous permettra d'obtenir une valeur exacte pour la valeur de \(\mathcal{A}\). Avec l'ajout de ces notions, on peut écrire :
On vient alors d'établir que la variable utilisée dans l'intégrale est muette comme l'indice présent dans une somme, mettre un \(y\) à la place de \(x\) et \(dy\) au lieu de \(dx\) ne changera pas la valeur de l'intégrale.
Remarque : Notons que la notation \(\int\) a été appliquée sur une fonction continue, si elle ne l'est pas, il sera possible de définir l'intégrale mais seulement si \(f\) n'est pas continue en des points au plus dénombrables (l'ensemble des points de discontinuités est dénombrable si ces points peuvent être numérotés avec un indice parcourant \(\mathbb{N}\)).
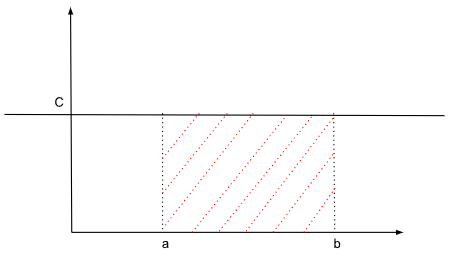
On peut, avec cette approche d'abord géométrique, calculer l'intégrale de certaines fonctions continues. Par exemple, si \(f\) est une fonction constante égale à \(C\) un réel alors elle est continue donc son intégrale est bien définie. L'intégrale sur \([a;b]\) de \(f\) revient alors à calculer l'aire d'un simple rectangle de hauteur \(C\) et de largeur \(b-a\). On peut donc écrire :
On retrouve la cohérence du résultat de l'intégrale avec le dessin suivant :
Observons maintenant quelques résultats sur ce nouvel opérateur, l'opérateur intégral : c'est un opérateur linéaire antisymétrique qui conserve la croissance.
Proposition 1. Opérations sur les intégrales
Soient \(f\) et \(g\) deux fonctions continues sur \([a;b]\subset\mathbb{R}\) et \(\lambda\) un réel.
1. L'intégrale en un point est nulle : \(\displaystyle \int_a^af=0\)
2. L'intégrale est antisymétrique : \(\displaystyle \int_a^bf=-\int_b^af\)
3. L'intégrale est linéaire : \(\displaystyle \int_a^b(f+g)=\int_a^bf+\int_a^bg\) et \(\displaystyle\int_a^b(\lambda f)=\lambda \int_a^bf\)
4. L'intégrale est croissante : si \(f\le g\) sur \([a;b]\) alors \(\displaystyle \int_a^bf\le\int_a^bg\)
Preuve
1. En partant de la définition de l'intégrale, on en déduit facilement le premier résultat (la longueur du domaine sur lequel on intègre est nulle).
2. Ce résultat est une simple conséquence du fait que \((b-a)=-(a-b)\) donc la longueur est la même à un signe près d'où l'apparition du signe moins.
3. En utilisant la définition naturelle de l'intégrale comme une somme d'aires de rectangles de largeur \(dx\) et de hauteur \(f(x)\), l'intégrale hérite alors de la linéarité de la somme.
4. Là encore, comme la somme est croissante, l'intégrale hérite à nouveau de cette croissance.
Comme on a eu une approche géométrique pour définir l'intégrale, on peut utiliser le fait que l'intégrale est une grandeur algébrique (positive ou négative) et que les longueurs peuvent être définies à partir de vecteurs pour appliquer la relation de Chasles par exemple.
Proposition 2. La relation de Chasles - version intégrale
Soient \(f\) une fonction continue sur \([a;b]\subset\mathbb{R}\) et \(c\in\mathbb{R}\) avec \(a
Preuve
Une démonstration possible consiste à utiliser le théorème 1.2. vu plus loin étant donné que les fonctions considérées sont continues. Si l'on note \(F\) une primitive de \(f\) alors on d'une part :
ce qui achève cette preuve.
Proposition 3. Positivité de l'intégrale et critère de nullité
Soit \(f\) une fonction positive et continue sur \([a;b]\subset\mathbb{R}\) et \(c\in\mathbb{R}\).
1. L'intégrale est positive : \(\displaystyle \int_a^bf\ge0\)
2. L'intégrale nulle d'une fonction positive : si \(\displaystyle \int_a^bf=0\) alors \(f=0\) sur \([a;b]\).
Preuve
1. Comme la fonction est positive, en utilisant la définition d'aire algébrique sous la courbe, c'est un argument qui permet de comprendre ce résultat. Une preuve mathématique consiste à utiliser à nouveau le théorème 1.2. Si l'on note \(F\) une primitive de \(f\) car \(f\) est continue, comme \(f\) est positive, il en suit que \(F\) est croissante car on rappelle que \(F\) a pour dérivée \(f\). Or comme \(a 2. A nouveau, avec les mêmes notations que précédemment, on a : Or \(F\) est croissante mais \(F(a)=F(b)\) donc \(F\) ne peut être que constante. Or \(F'=f\) mais si \(F\) est constante alors \(F'=0\) d'où :
Définition 1. Valeur moyenne d'une fonction continue
Soit \(f\) une fonction continue sur \([a;b]\subset\mathbb{R}\). On définit sa valeur moyenne sur \([a;b]\) notée \(\mu_{[a;b]}(f)\) comme :
Proposition 4. Inégalité de la moyenne - version intégrale
Soit \(f\) une fonction continue sur \([a;b]\subset\mathbb{R}\).
S'il existe \(m\) et \(M\) deux réels tels que \(m\le f\le M\) sur \([a;b]\) alors on a l'inégalité suivante :
Cette inégalité est appelée l'inégalité de la moyenne ou inégalité de la valeur moyenne.
Preuve
Supposons que sur \([a;b]\), on a : \(m\le f\le M\). Comme l'intégrale est croissante d'après la proposition 1 et que les fonctions \(f\), \(x\mapsto m\) et \(x\mapsto M\) sont continues sur \([a;b]\), on peut écrire :
2. L'intégrale (au sens analytique)
Après avoir vu quelques résultats intéressants sur l'intégrale au sens géométrique, nous allons dans cette section unifier le concept de primitive avec la notion d'intégrale à l'aide du théorème qui suit, le théorème fondamental de l'analyse.
Théorème 1.1. Théorème fondamental de l'analyse - version intégrale
Soit \(f\) une fonction continue sur \([a;b]\subset\mathbb{R}\).
La fonction \(\displaystyle x\mapsto \int_a^xf\) définie sur \([a;b]\) est l'unique primitive de \(f\) s'annulant en \(a\).
Théorème 1.2. Théorème fondamental de l'analyse - version primitive
Soient \(f\) une fonction continue sur \([a;b]\subset\mathbb{R}\) et \(F\) une de ses primitives. Le théorème énonce :
En général, c'est plutôt la seconde version, la version primitive du théorème fondamental de l'analyse qu'on utilise. C'est lui qui indique clairement le lien entre la construction géométrique de l'intégrale qu'on en a faite et sa corrélation avec la notion de primitive. On comprend mieux alors la nécessité d'avoir continuité pour l'intégrande.
Remarque : L'intégrande désigne la fonction que l'on intègre, qui se trouve à l'intérieur de l'intégrale.
Ainsi, connaissant les primitives usuelles (de fonctions usuelles, de fonctions composées), on peut réaliser un bon nombre de calculs mettant en jeu la manipulation d'intégrales. De manière inverse, on peut à partir de la valeur de l'intégrale d'une fonction, déterminer une primitive de cette fonction à une constante près. C'était l'objet du théorème 1.1. Dans la suite, on s'intéresse alors à un théorème concernant les intégrales et leur valeur.
Théorème 2. Théorème intégration par parties
Soient \(u\) et \(v\) deux fonctions dérivables de dérivées continues sur \([a;b]\subset\mathbb{R}\). Le théorème énonce :
avec \([uv]_a^b=u(b)v(b)-u(a)v(a)\).
Preuve
Avec les hypothèses de l'énoncé, la fonction \(uv\) est dérivable sur \([a;b]\) d'où :
\[ (uv)'=u'v+uv' \]Comme \(u\), \(u'\), \(v\) et \(v'\) sont continues alors les fonctions \((uv)'\), \(u'v\) et \(uv'\) sont continues par produit. Leur intégrale est bien définie donc on peut écrire :
\[ \int_a^b(uv)'=\int_a^b(u'v+uv') \iff \int_a^b(uv)'=\int_a^bu'v+\int_a^buv' \]Il est aisé de dire que \(uv\) est une primitive de \((uv)'\) par définition donc on a :
\[ \int_a^b(uv)'=[u(x)v(x)]_a^b=u(b)v(b)-u(a)v(a) \]On a bien alors que :
ce qui achève cette démonstration.
Remarque : Ce théorème permet de déterminer les primitives de certaines fonctions dont la forme n'est pas connue avec les formulaires vus en cours. Par exemple, c'est avec ce théorème qu'on détermine les primitives des fonctions de la forme \(x\mapsto x^n\) pour \(n\) un entier naturel.
3. Calcul de volume
On peut utiliser l'intégrale pour calculer des volumes en trois dimensions. Si l'on considère le problème suivant : on cherche à déterminer le volume du solide engendré par la rotation de la courbe d'une fonction \(f\) continue par rapport à l'axe des abscisses (axe de révolution) sur le domaine \([a;b]\subset\mathbb{R}\).
Pour ce faire, il suffit d'intégrer sur \([a;b]\), la section droite par rapport à l'axe des abscisses du solide engendré par rotation. Cette section en un point \(x\in[a;b]\) a pour aire \(\pi f^2(x)\) étant donné que sur cette section, \(f\) prend la valeur constante égale à \(x\). Ainsi, le volume noté \(\mathcal{V}\) du solide engendré par rotation de la courbe représentative de \(f\) sur \([a;b]\) est donné par la relation suivante :
On résume cela dans la proposition suivante :
Proposition 5. Volume d'un solide engendré par rotation
Soit \(f\) une fonction continue sur \([a;b]\subset\mathbb{R}\).
La rotation de la courbe représentative de la fonction \(f\) autour de l'axe des abscisses sur l'intervalle \([a;b]\) engendre un solide de volume noté \(\mathcal{V}\) donné par la formule suivante :
Preuve
Comme application, retrouvons le volume d'un cylindre noté \(\mathcal{V}\) avec cette formule. Pour cela, on considère la fonction \(f:x\mapsto r\) où \(r\) est une constante représentant plus tard le rayon du cylindre. On définit cette fonction sur l'intervalle \([a;b]\) de longueur notée \(H\) qu'on pourra voir plus tard comme la hauteur du cylindre.
Si l'on intègre la fonction \(f\) qui est continue en tant que fonction constante sur \([a;b]\) à l'aide de la formule précédente, on a :
On a bien retrouvé le volume d'un cylindre de rayon \(r\) et de hauteur \(H\).
Un second exemple plus sophistiqué est de retrouver le volume d'une sphère noté \(\mathcal{V}\) de rayon \(r\). Pour trouver la bonne fonction \(f\) qui aboutira à la détermination d'un tel volume, il faut remarquer qu'une section de sphère est un cercle de rayon \(r\). Ainsi, si l'on trace un rayon sur ce cercle, le théorème de Pythagore permet d'écrire :
\[ f^2(x)+x^2=r^2 \iff f^2(x)=r^2-x^2 \]En utilisant alors la formule précédente, on en déduit que :
Finalement, on conclut avec le célèbre résultat :
Remarque : Comme on peut le faire avec des fonctions continues pour les aires, on peut déterminer le volume du solide engendré entre deux fonctions continues notées \(f\) et \(g\). Le volume noté \(\mathcal{V}\) du solide engendré entre les courbes représentatives des fonctions continues \(f\) et \(g\) sur \([a;b]\) a pour expression :
\[ \mathcal{V}=\pi\int_a^b\left[f^2(x)-g^2(x)\right]dx \]Rappelons que pour déterminer l'aire noté \(\mathcal{A}\) entre les courbes représentatives de \(f\) et de \(g\) sous les mêmes hypothèses de continuité sur \([a:b]\) a pour expression :
\[ \mathcal{A}=\int_a^b\left[f(x)-g(x)\right]dx \]