Terminale : Étude de fonctions
Dans ce chapitre, nous allons voir la méthode à suivre lorsque l'on doit étudier une fonction - en d'autres termes, nous allons appliquer l'ensemble des outils vus tout au long de l'année pour réaliser une étude complète des fonctions.
D'abord, définissons la notion de fonction.
📚 Table des matières
Définition 1. Fonction réelle
Une fonction réelle \(f\) est un objet mathématique qui, à un réel \(x\), associe un réel \(f(x)\). On dit que \(x\) est l'antécédent par \(f\) de l'image \(f(x)\).
1. Première étape - Détermination de l'ensemble de définition
Si l'on considère une fonction \(f\), il faut déterminer l'ensemble des valeurs qu'on note \(\mathcal{D}_f\) pour lequel, \(f(x)\) a un sens lorsque \(x\in\mathcal{D}_f\). On parle d'ensemble de définition.
En pratique, il faut connaître l'ensemble de définition des fonctions usuelles afin d'en déduire l'ensemble de définition des fonctions plus sophistiquées. Par exemple, posons \(f\) la fonction suivante :
\[ f:x\mapsto \ln\left(\dfrac{x^2+1}{x^2-1}\right) \]La fonction \(f\) n'est pas évidente puisqu'elle s'écrit comme une composée de différentes fonctions : logarithme d'une quotient dont le dénominateur et le numérateur sont un polynôme du second degré. Nous déterminerons, dans ce cas, l'ensemble de définition de la fonction \(f\) dans un prochain exemple.
Dans le suite, \(u\) et \(v\) désigne deux fonctions dont leur ensemble de définition s'écrit \(\mathcal{D}_u\) et \(\mathcal{D}_v\) respectivement.
Proposition 1. Ensemble de définition d'un produit
L'ensemble de définition du produit \(uv\) est égal à \(\mathcal{D}_u \cap \mathcal{D}_v\).
Preuve
Dans d'autres termes, cela veut dire que l'on prend les valeurs communes dans \(\mathcal{D}_u\) et \(\mathcal{D}_v\) pour définir leur produit. Pour le démontrer, rien de plus simple :
Soit \(\mathcal{D}_{uv}\) l'ensemble de définition de la fonction produit \(uv\). On veut montrer que :
\[ \mathcal{D}_{uv}=\mathcal{D}_u \cap \mathcal{D}_v \]Soit \(x\in\mathcal{D}_{uv}\). Le nombre \((uv)(x)\) est bien défini, qu'on peut réécrire \(u(x)\cdot v(x)\) ainsi les nombre \(u(x)\) et \(v(x)\) existent : cela signifie que \(x\in\mathcal{D}_u\) et \(x\in\mathcal{D}_v\). D'où : \(\mathcal{D}_{uv}\subset\mathcal{D}_u \cap \mathcal{D}_v\).
Réciproquement, si \(x\in \mathcal{D}_u \cap \mathcal{D}_v\) alors \(x\in\mathcal{D}_u\) et \(x\in\mathcal{D}_v\). Donc les nombres \(u(x)\) et \(v(x)\) sont bien définis. On en déduit alors que le produit \(u(x)v(x)=(uv)(x)\) existe. On a bien que \(x\in\mathcal{D}_{uv}\). D'où : \(\mathcal{D}_u \cap \mathcal{D}_v\subset \mathcal{D}_{uv}\).
Cela conclut notre démonstration. On vient d'établir l'égalité d'ensembles.
Remarque : Le symbole logique \(\subset\) désigne « être inclus dans ».
Soit \(f\) une fonction réelle définie sur \(\mathcal{D}_f\subset \mathbb{R}\). On note \(\mathcal{O}_f\) l'ensemble des zéros de la fonction, c'est-à-dire l'ensemble des valeurs \(x\in\mathcal{D}_f\) tel que \(f(x)=0\). On notera alors \(\mathcal{D}_v^*\) l'ensemble des valeurs \(x\in\mathcal{D}_v\) telles que \(f(x)\ne0\). En fait, on peut écrire :
\[ \mathcal{D}_v=\mathcal{D}_v^* \cup \mathcal{O}_f \textrm{ avec } \mathcal{D}_v^* \cap \mathcal{O}_f=\emptyset \implies \mathcal{D}_v^* = \mathcal{D}_v \backslash \mathcal{O}_f \]où \(\cup\) désigne l'union (le "ou"), \(\cap\) désigne l'intersection (le "et"), \(\emptyset\) désigne l'ensemble vide (le "rien") et \(\backslash\) désigne la différence (le "excluant").
Proposition 2. Ensemble de définition d'un quotient
L'ensemble de définition du produit \(\frac{u}{v}\) est égal à \(\mathcal{D}_u \cap \mathcal{D}_v^*\).
En détail, on peut écrire :
\[ \mathcal{D}_u \cap \mathcal{D}_v^*=\mathcal{D}_u \cap \{x\in\mathcal{D}_v \textrm{ tel que }v(x)\ne0\}= \{x\in \mathbb{R} \textrm{ tel que }u(x)\in\mathbb{R}\} \cap \{x\in \mathbb{R} \textrm{ tel que }v(x)\in\mathbb{R}^*\} \]En ce qui concerne la preuve de cette proposition, elle est identique à la précédente.
Soient \(f\) et \(g\) deux fonctions réelles définies sur \(\mathcal{D}_f\subset \mathbb{R}\) et \(\mathcal{D}_g\subset \mathbb{R}\) respectivement. Pour définir la fonction composée \(f\circ g=f(g)\), il faut que l'ensemble des valeurs réelles \(x\) choisies au départ, \(g(x)\) doit appartenir à \(\mathcal{D}_f\) pour que \(f(g(x))\) existe. Ainsi, on définit l'ensemble \(\mathcal{D}_g^f\) de telle façon que :
\[ \mathcal{D}_g^f=\{x\in\mathcal{D}_g \textrm{ tel que }g(x)\in\mathcal{D}_f\} \]Ainsi, dans ce cas, la fonction composée \(f\circ g\) est bien définie.
Proposition 3. Ensemble de définition d'une composée
L'ensemble de définition de la composée \(u\circ v\) est égal à \(\mathcal{D}_v^u\).
Exemple 1.
Donner l'ensemble de définition de la fonction \(f\) suivante :
\[ f:x\mapsto \ln\left(\dfrac{x^2+1}{x^2-1}\right) \]On veut déterminer les réels \(x\) tels que \(f(x)\) existe. Ici l'on remarque que la fonction \(f\) est la composée \(u\circ v\) avec :
\[ u:x\mapsto \ln(x) \quad \textrm{et} \quad v:x\mapsto \dfrac{x^2+1}{x^2-1} \]On remarque que \(u\) est une forme usuelle dont l'ensemble de définition est \(]0;+\infty[\). Donc : \(\mathcal{D}_u=]0;+\infty[\).
D'autre part, \(v\) s'écrit comme un quotient \(\frac{q}{s}\) avec :
\[ q:x\mapsto x^2+1 \quad \textrm{et} \quad s:x\mapsto x^2-1 \]Ainsi, pour définir \(v\), il faut déterminer l'ensemble : \(\mathcal{D}_q \cap \mathcal{D}_s^*\). Comme \(q\) et \(s\) sont des polynômes, \(\mathcal{D}_q=\mathbb{R}\) et \(\mathcal{D}_s=\mathbb{R}\).
Pour déterminer \(\mathcal{D}_s^*\), il faut déterminer les valeurs réelles \(x\) telles que \(s(x)=0\) :
\[ s(x)=0 \iff x^2-1=0 \iff (x+1)(x-1)=0 \iff x=\pm 1 \]Il en suit que : \(\mathcal{D}_s^*=\mathbb{R}\backslash \{-1,+1\}\). Finalement, on obtient l'ensemble de définition de \(v\) : \(\mathcal{D}_v = \mathbb{R}\backslash \{-1,+1\}\).
Pour correctement définir \(f=u\circ v\), il faut déterminer :
\[ \mathcal{D}_v^u=\{x\in\mathcal{D}_v \textrm{ tel que }v(x)\in\mathcal{D}_u\}=\{x\in\mathbb{R}\backslash \{-1,+1\} \textrm{ tel que }v(x)\in]0;+\infty[\} \]Il suffit donc de résoudre \(v(x)>0\). Comme \(v\) s'écrit comme un quotient, il suffit d'étudier le signe de \(q\) et de \(s\).
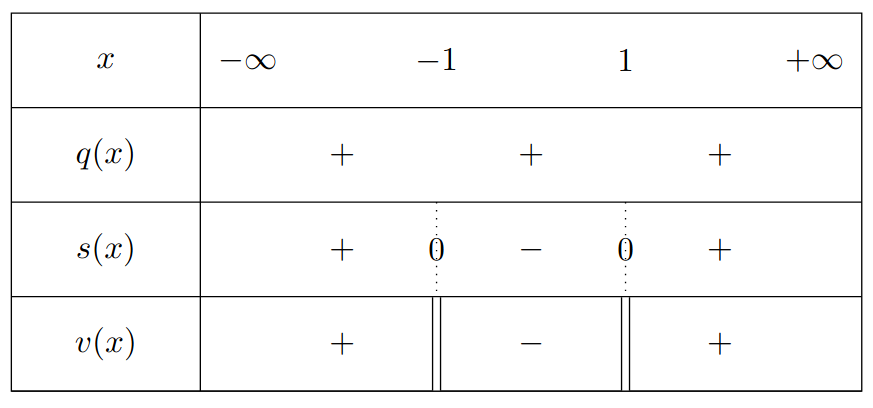
Ainsi, pour tout \(x\in]-\infty;-1[\cup]1;+\infty[\), \(v(x)>0\). On en déduit alors que :
2. Seconde étape - Détermination de l'ensemble de dérivabilité
Après avoir déterminé l'ensemble de définition d'une fonction réelle \(f\), il nous faut maintenant déterminer son ensemble de dérivabilité. C'est l'ensemble des valeurs pour lesquelles la forme dérivée de \(f\), notée en général \(f'\), est bien définie.
Pour cela, nous devons connaître les ensemble de dérivabilité des fonctions au sens classique pour ensuite opérer sur des formes produit, quotient ou encore composée.
Avant, rappelons la définition de la fonction dérivée d'une fonction \(f\) en un point de son ensemble de définition :
Définition 2.
Soit \(a\in\mathcal{D}_f\). Si le taux d'accroissement de \(f\) en \(a\) admet une limite finie en \(a\) alors celle-ci est appelée nombre dérivée de \(f\) en \(a\) et on la note \(f'(a)\).
On dit alors que \(f\) est dérivable en \(a\).
Maintenant, en admettant les ensembles de dérivabilité des fonctions connues, nous avons les propriétés suivantes semblables aux précédentes pour l'ensemble de définition. Si l'on note \(\mathcal{D}_f\) l'ensemble de définition d'une fonction réelle \(f\) alors on notera \(\mathcal{D}_f'\) son ensemble de dérivabilité. On a bien sûr : \(\mathcal{D}_f'\subset \mathcal{D}_f\).
Proposition 4. Ensemble de dérivabilité d'un produit
L'ensemble de dérivabilité du produit \(uv\) est égal à \(\mathcal{D}_u '\cap \mathcal{D}_v'\).
Proposition 5. Ensemble de dérivabilité d'un quotient
L'ensemble de dérivabilité du produit \(\frac{u}{v}\) est égal à \(\mathcal{D}_u' \cap \mathcal{D}_v'^*\).
Proposition 6. Ensemble de dérivabilité d'une composée
L'ensemble de dérivabilité de la composée \(u\circ v\) est égal à \(\tilde{\mathcal{D}}_{v}^{u}\).
Ici, nous devons donner un sens à l'ensemble \(\tilde{\mathcal{D}}_{v}^{u}\). Si \(u\) et \(v\) sont dérivables, alors :
\[ (u\circ v)'=v' \cdot (u'\circ v) \]Donc, on en déduit que le réel \(v'(x)\) et \((u'\circ v)(x)\) doivent exister. En utilisant les propositions 1 et 3, on a :
\[ \tilde{\mathcal{D}}_{v}^{u}=\mathcal{D}_v' \cap \mathcal{D}_v^{u'} \]Ainsi, il en suit que :
\[ \tilde{\mathcal{D}}_{v}^{u}=\mathcal{D}_v'\cap\{x\in\mathcal{D}_v \textrm{ tel que }v(x)\in\mathcal{D}_u'\} \]Remarque : En pratique, les ensembles de dérivabilité ne diffèrent pas tellement des ensembles de définition sauf lorsque les fonctions \(x\mapsto \sqrt{x}\) ou \(x\mapsto|x|\) apparaissent. Elles ne sont pas dérivables en 0.
Rappel : Rappelons que si une fonction est dérivable sur un intervalle, elle y est continue. Cela permet de justifier d'une autre manière certains ensembles de continuité en passant par la dérivée.
3. Troisième étape - Étude des variations d'une fonction réelle
Après avoir déterminé l'ensemble de dérivabilité d'une fonction réelle \(f\), nous pouvons calculer sa dérivée \(f'\). Pour déterminer ses variations, il nous faut étudier le signe de la dérivée.
Théorème 1.
Soient \(f\) une fonction réelle dérivable sur \(\mathcal{D}_f'\).
1. \(f\) est croissante sur \(\mathcal{I}\subset\mathcal{D}_f'\) si et seulement si \(\forall x\in\mathcal{I}\subset\mathcal{D}_f',f'(x)\ge0\).
2. \(f\) est décroissante sur \(\mathcal{I}\subset\mathcal{D}_f'\) si et seulement si \(\forall x\in\mathcal{I}\subset\mathcal{D}_f',f'(x)\le0\).
En général, la représentation usuelle est de construire le tableau de signe de la dérivée \(f'\) et en dessous, le tableau de variation de \(f\).
4. Quatrième étape - Étude des extremums d'une fonction réelle
Après avoir obtenu le tableau de variation, il est possible d'identifier les points pour lesquels, la dérivée est nulle. Ces points représentent des extremums locaux ou globaux. Si l'on note \(a\), l'abscisse d'un des extremums d'une fonction alors \(f(a)\) est un maximum ou minimum local ou global.
Définition 3.
Soient \(f\) une fonction réelle définie sur \(\mathcal{D}_f\), \(\mathcal{I}\subset\mathcal{D}_f'\) et \(a\in\mathcal{I}\).
1. On dit qu'en \(x=a\), \(f\) admet un maximum local sur \(\mathcal{I}\) lorsque \(\forall x\in\mathcal{I},f(x)\le f(a)\). Si \(\mathcal{I}=\mathcal{D}_f\) alors on parle de maximum global.
2. On dit qu'en \(x=a\), \(f\) admet un minimum local sur \(\mathcal{I}\) lorsque \(\forall x\in\mathcal{I},f(x)\ge f(a)\). Si \(\mathcal{I}=\mathcal{D}_f\) alors on parle de minimum global.
3. On dit qu'en \(x=a\), \(f\) admet un extremum local sur \(\mathcal{I}\) si en \(x=a\), \(f\) admet un maximum local ou un minimum local. Si \(\mathcal{I}=\mathcal{D}_f\) alors on parle d'extremum global.
Le lien entre position des extremums potentiels et dérivée est le suivant :
Théorème 2.
Soient \(f\) une fonction réelle dérivable sur \(\mathcal{D}_f'\) et \(a\in\mathcal{D}_f'\).
1. Si \(f\) admet un extremum local en \(x=a\) alors \(f'(a)=0\).
2. Si \(f'(a)=0\) et \(f'\) change de signe en \(a\) alors \(u\) admet un extremum local en \(x=a\).
5. Cinquième étape - Calcul des limites d'une fonction réelle
Lorsqu'on a l'ensemble de définition d'une fonction réelle \(f\), on peut déterminer les limites aux bornes de cet ensemble de définition.
Lorsqu'on calcule une limite, on cherche à savoir si la forme de fonction étudiée est usuelle ou représente une forme indéterminée : la résolution du premier cas est triviale ; la seconde amène à une réflexion - quelle technique doit-on utiliser pour trouver la limite cherchée ?
Pour cela nous avons plusieurs outils : théorème des gendarmes, théorème de minoration/majoration, multiplication par la forme conjuguée, reconnaître un taux d'accroissement, théorème des croissances comparées, etc.
6. Sixième étape - Étude de la convexité d'une fonction réelle
Pour étudier la convexité d'une fonction réelle \(f\), il faut s'assurer que l'ensemble de définition de la dérivée seconde soit établie. Passer cela, il faut calculer la dérivée seconde de la fonction, notée \(f''\) puis étudier son signe. Le signe de \(f''\) donne la convexité de \(f\).
L'étude de la convexité permet d'établir quelques résultats intéressants : par exemple, une fonction convexe est toujours au-dessus de ses tangentes. L'étude de la convexité permet donc d'avoir une meilleure visualisation des courbes de la fonction.
Théorème 3.
Soient \(f\) une fonction réelle dérivable deux fois sur \(\mathcal{D}_f''\) et \(a\in\mathcal{D}_f''\).
1. \(\forall x\in\mathcal{I}\subset\mathcal{D}_f'',f''(x)>0\) si et seulement si \(f\) est convexe sur \(\mathcal{I}\).
2. \(\forall x\in\mathcal{I}\subset\mathcal{D}_f'',f''(x)<0\) si et seulement si \(f\) est concave sur \(\mathcal{I}\).
3. Si \(f''(a)=0\) et \(f''\) change de signe en \(x=a\) alors \(a\) est un point d'inflexion de \(f\).
7. Septième étape - Tracé du graphe d'une fonction réelle
En général, pour tracer l'allure d'une courbe d'une fonction réelle \(f\), il faut être rigoureux. D'abord, il faut tracer les asymptotes horizontales ou verticales (si elles existent). Ensuite, en calculant l'image de quelques points, déterminons l'équation de certaines tangentes, repérer les extremums (= tangente horizontale), adapter l'allure de la courbe en fonction de la convexité de \(f\).
Exemple 2.
Réaliser l'étude complète de la fonction suivante :
\[ f:x\mapsto \dfrac{\ln(x)}{x} \]Ensemble de définition :
La fonction \(f\) s'écrit comme un quotient. Le numérateur \(\ln(x)\) est défini sur \(]0;+\infty[\). Le dénominateur \(x\) est défini sur \(\mathbb{R}\) et s'annule en \(0\). L'ensemble de définition est donc l'intersection de \(]0;+\infty[\) et \(\mathbb{R}^*\), ce qui donne :
Dérivabilité et variations :
\(f\) est dérivable sur \(]0;+\infty[\) en tant que quotient de fonctions dérivables. On a :
Le signe de \(f'(x)\) ne dépend que de \(1-\ln(x)\) car \(x^2 > 0\) sur \(\mathcal{D}_f\).
\(1-\ln(x) > 0 \iff 1 > \ln(x) \iff e > x\).
\(1-\ln(x) = 0 \iff x = e\).
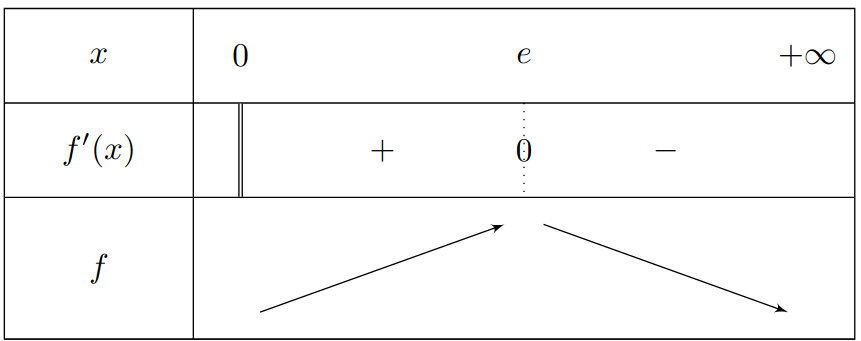
Limites et tableau complet :
- En \(0^+\) : \(\lim\limits_{x \rightarrow 0^+}\ln(x)=-\infty\) et \(\lim\limits_{x \rightarrow 0^+}\frac{1}{x}=+\infty\). Par produit, \(\lim\limits_{x \rightarrow 0^+}f(x)=-\infty\).
- En \(+\infty\) : Par croissance comparée, \(\lim\limits_{x \rightarrow +\infty}f(x)=0\).
- On a \(f(e) = \frac{\ln(e)}{e} = \frac{1}{e}\).
On peut alors compléter le tableau de variation :
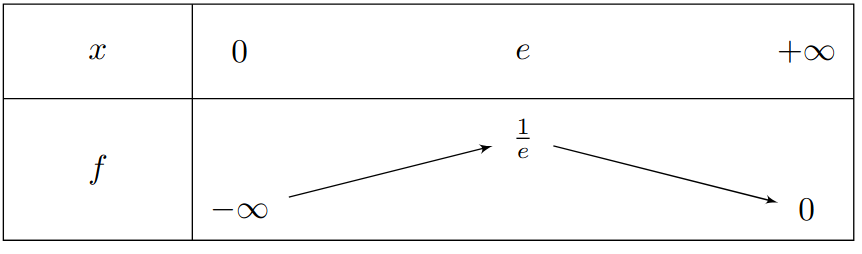
On remarque qu'en \(x=e\), \(f\) atteint un maximum global \(\frac{1}{e}\).
Convexité :
On calcule la dérivée seconde sur \(]0;+\infty[\) :
Le signe de \(f''(x)\) ne dépend que de \(2\ln(x)-3\) car \(x^3 > 0\).
\(2\ln(x)-3 = 0 \iff \ln(x) = \frac{3}{2} \iff x = e^{3/2}\).
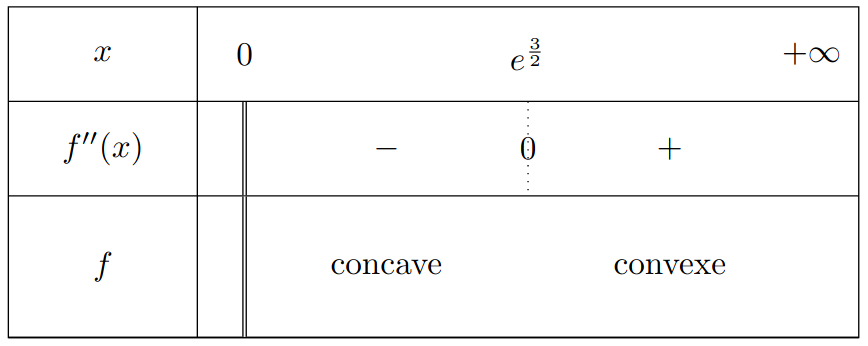
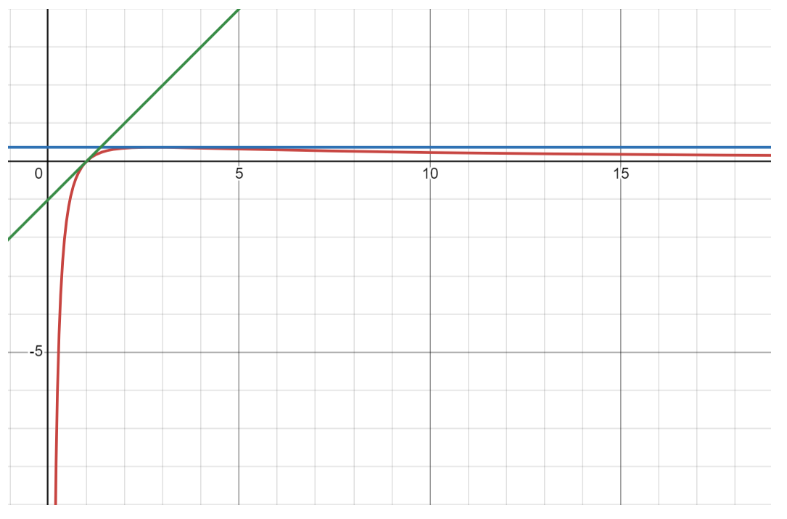
Tracé :
On trace le graphe de la fonction \(f\) (en rouge), avec sa tangente en \(x=1\) (verte, \(y=x-1\)) et sa tangente horizontale en \(x=e\) (bleue, \(y=1/e\)).
Remarque : Nous vous recommandons néanmoins d'aller voir les différents cours en lien avec les différentes notions discutées pour compléter vos outils d'analyse : dérivation, calcul de limite, continuité et convexité.