Terminale : Dérivabilité
Dans tout ce chapitre, on définit \(I\) et \(J\) comme des intervalles de \(\mathbb{R}\).
📚 Table des matières
1. Définitions
Soient \(a \in I\) et \(f : I \mapsto \mathbb{R}\) :
Rappel (Taux d'accroissement).
On appelle taux d'accroissement de la fonction \(f\) en \(a\), la fonction \(\Delta\) définie par :
Définition 2 (Dérivabilité en un point).
On dit que \(f\) est dérivable en \(a\) si :
Autrement dit, il faut que la limite du taux d'accroissement de \(f\) en \(a\) existe et soit finie. Ce nombre est appelé nombre dérivé de \(f\) en \(a\) et est noté \(f'(a)\).
Interprétation graphique.
Si \(\displaystyle\lim_{x \to a} \frac{f(x)-f(a)}{x-a}\) est finie, alors la droite d'équation \(y=f'(a) (x-a) + f(a)\) est appelée tangente de \(f\) en \(a\).
Dans le cas où \(\displaystyle\lim_{x \to a} \frac{f(x)-f(a)}{x-a} = \pm \infty\), la droite d'équation \(x=a\) est appelée tangente de \(f\) en \(a\).
Graphiquement, comme \(f'(a)\) représente le coefficient directeur de la tangente en \(a\) de \(f\), on a bien deux cas :
.png)
Figure 1. \(x \mapsto \sqrt{x}\)
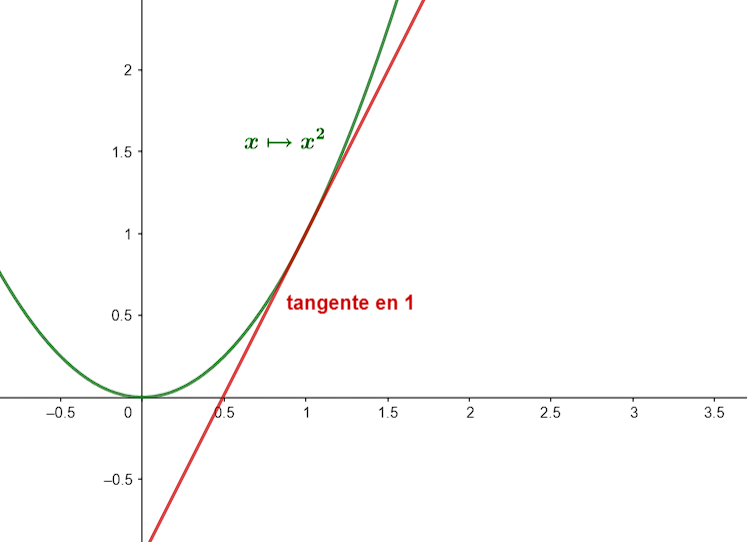
Figure 2. \(x \mapsto x^2\)
Dans le cas de \(x \mapsto \sqrt{x}\), le coefficient directeur de la tangente en 0 vaut \(+\infty\), donc cette fonction n'est pas dérivable en 0. Néanmoins, pour \(x \mapsto x^2\), le coefficient directeur est fini, donc cette fonction est dérivable en 1.
2. Opérations sur les fonctions dérivables
On s'intéresse désormais aux différentes propriétés de la dérivée.
Propriété 3 (Opérations usuelles).
Pour \(f:I \to \mathbb{R}\), \(g:I \to \mathbb{R}\) dérivables et \(a \in I\) :
- Addition : \(f+g\) est dérivable en \(a\) et : \[ (f+g)'(a) = f'(a) + g'(a) \]
- Combinaison linéaire : En généralisant, pour \(\lambda\) et \(\beta\) deux réels, \(\lambda f + \beta g\) est dérivable en \(a\) et : \[ (\lambda f + \beta g)'(a) = \lambda f'(a) + \beta g'(a) \]
- Multiplication : \(fg\) est dérivable en \(a\) et : \[ (fg)'(a) = f'(a) g(a) + f(a) g'(a) \]
- Quotient : Si \(g(a)\) est non nul, alors \(\frac{f}{g}\) est dérivable en \(a\) et : \[ \left(\frac{f}{g}\right)'(a) = \frac{f'g-fg'}{g^2} \]
Exemple 1.
Considérons la fonction \(f : x \mapsto e^{2x}\). Déterminer le domaine de dérivabilité de \(f\) et la dérivée de \(f\).
Correction
Ici, remarquons que \(f(x) = e^x \times e^x\) et la fonction exponentielle est dérivable sur \(\mathbb{R}\) donc par produit de fonctions dérivables, on en déduit que \(f\) est dérivable sur \(\mathbb{R}\). Par définition de l'exponentielle : \(\exp' = \exp\). Finalement, d'après le résultat précédent pour \(x \in \mathbb{R}\) :
\[ f'(x) = e^x e^x + e^x e^x = 2 e^x e^x = 2 e^{2x} \]
On remarque dans l'exemple précédent que \(f\) peut aussi s'interpréter comme la composée de deux fonctions. En effet : \[ f=\exp \circ g \] où \(g:x \mapsto 2x\). Dès lors, le résultat suivant est bien utile :
Propriété 4 (Composition).
Soient \(a \in I\), \(f : I \to J\) dérivable en \(a\) et \(g : J \to \mathbb{R}\) dérivable en \(f(a)\), alors \(g \circ f : I \to \mathbb{R}\) est dérivable en \(a\) et :
3. Croissance et monotonie
Une fois la notion de dérivabilité maîtrisée, il est désormais temps d'en faire usage. Dans cette section, on s'intéresse aux résultats établis grâce au caractère dérivable d'une fonction.
Théorème 3.
Soit \(f:I \to \mathbb{R}\) dérivable :
On en déduit alors un résultat plus général permettant de caractériser entièrement la monotonie d'une fonction à l'aide de sa dérivée :
Théorème 4 (Monotonie à l'aide de la dérivée).
Soit \(f:I \to \mathbb{R}\) une fonction dérivable :
Un résultat plus fort sur la stricte monotonie permet de caractériser encore mieux les variations d'une fonction dérivable :
Théorème 5 (Stricte monotonie à l'aide de la dérivée).
Soit \(f:I \to \mathbb{R}\) une fonction dérivable :
Remarque : En règle générale, on utilise simplement l'implication suivante :
\(f'\) est strictement positive sur I \(\implies\) \(f\) est strictement croissante sur I