Tale Spécialité : Mathématiques : Convexité
Dans ce chapitre, nous allons étudier une propriété importante des fonctions : la convexité. Cette notion va nous permettre de mieux comprendre la forme des courbes et d'établir des inégalités utiles. Nous travaillerons sur un intervalle \(I\) de \(\mathbb{R}\).
📚 Table des matières
1. Notion de sécante (rappels et compléments)
Pourquoi commencer par les sécantes ? La convexité d'une fonction se définit en comparant la courbe avec ses sécantes. Il est donc essentiel de bien maîtriser cette notion avant d'aller plus loin.
Définition 1. (Sécante et corde)
Soit \(f\) une fonction définie sur un intervalle \(I\), et soient \(a\) et \(b\) deux réels de \(I\) avec \(a < b\).
1. La sécante à la courbe de \(f\) passant par les points \(A(a; f(a))\) et \(B(b; f(b))\) est la droite \((AB)\).
2. La corde est le segment \([AB]\) reliant ces deux points.
L'équation de cette sécante est :
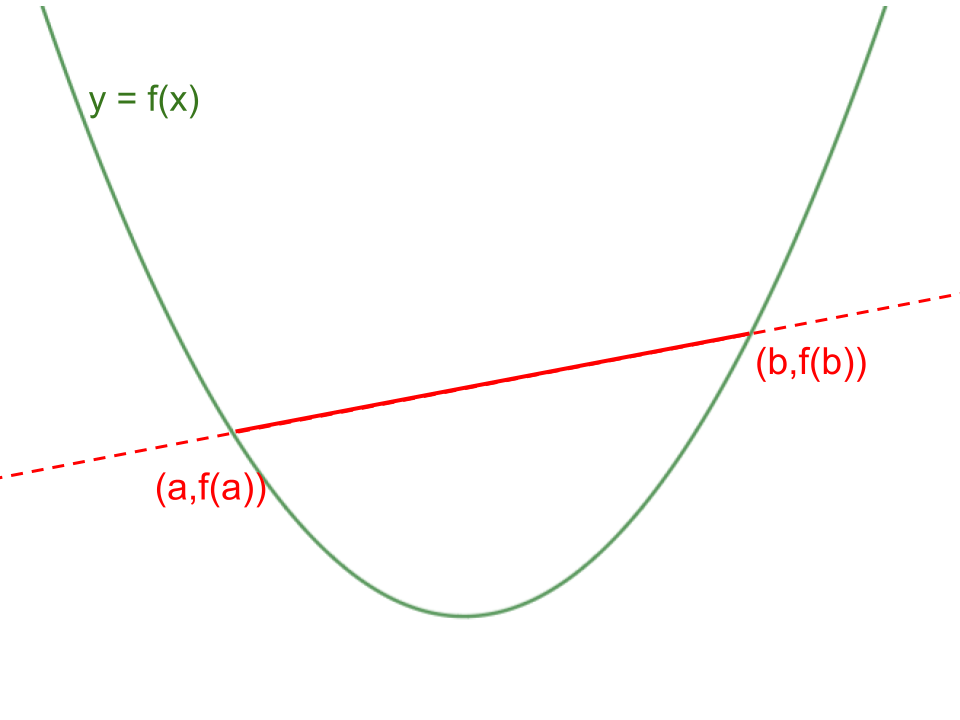
Figure 1. Sécante (droite complète) et corde (segment) entre deux points
Lien avec la notion de segment : Pour bien comprendre la convexité, nous avons besoin de décrire tous les points situés entre \(a\) et \(b\) de manière pratique.
Définition 2. (Combinaison convexe)
Pour deux réels \(a\) et \(b\) avec \(a \leq b\), tout point \(x\) du segment \([a,b]\) peut s'écrire sous la forme :
On dit que \(x\) est une combinaison convexe de \(a\) et \(b\).
Pourquoi cette écriture ? Quand \(\lambda = 0\), on obtient \(x = a\). Quand \(\lambda = 1\), on obtient \(x = b\). Pour les valeurs intermédiaires de \(\lambda\), on obtient tous les points entre \(a\) et \(b\). Cette écriture va être très utile pour définir la convexité.
2. Définition de la convexité
L'idée intuitive : Une fonction est convexe quand sa courbe "fait le dos rond" vers le haut. Mathématiquement, cela signifie que la courbe se situe toujours en-dessous de ses sécantes.
Définition 3. (Fonction convexe)
Une fonction \(f\) définie sur un intervalle \(I\) est dite convexe sur \(I\) si :
Pour tous \(a, b \in I\) et pour tout \(\lambda \in [0,1]\) :
Interprétation graphique : La courbe de \(f\) est située en-dessous de toutes ses sécantes.
Définition 4. (Fonction concave)
Une fonction \(f\) définie sur un intervalle \(I\) est dite concave sur \(I\) si :
Pour tous \(a, b \in I\) et pour tout \(\lambda \in [0,1]\) :
Interprétation graphique. La courbe de \(f\) est située au-dessus de toutes ses sécantes.
Remarque : Une fonction \(f\) est concave si et seulement si \(-f\) est convexe. Nous nous concentrerons donc principalement sur les fonctions convexes.
3. Caractérisation par la dérivée seconde
Pourquoi utiliser la dérivée seconde ? En pratique, vérifier directement la définition de la convexité est souvent difficile. La dérivée seconde nous donne un critère beaucoup plus simple à utiliser.
Théorème 1. (Critère de convexité)
Soit \(f\) une fonction deux fois dérivable sur un intervalle \(I\).
1. \(f\) est convexe sur \(I\) si et seulement si \(f''(x) \geq 0\) pour tout \(x \in I\)
2. \(f\) est concave sur \(I\) si et seulement si \(f''(x) \leq 0\) pour tout \(x \in I\)
Comment retenir ce critère ?
1. \(f''(x) > 0\) : la dérivée première \(f'\) est croissante, donc la courbe "tourne vers le haut" \(\Rightarrow\) convexe
2. \(f''(x) < 0\) : la dérivée première \(f'\) est décroissante, donc la courbe "tourne vers le bas" \(\Rightarrow\) concave
Exemple 1.
Étudions la convexité de \(f(x) = x^2\) sur \(\mathbb{R}\).
\(f'(x) = 2x\) et \(f''(x) = 2\)
Puisque \(f''(x) = 2 > 0\) pour tout \(x \in \mathbb{R}\), la fonction \(f(x) = x^2\) est convexe sur \(\mathbb{R}\).
Exemple 2.
Étudions la convexité de \(g(x) = \ln(x)\) sur \(]0; +\infty[\).
\[g'(x) = \frac{1}{x} \text{ et } g''(x) = -\frac{1}{x^2}\]
Puisque \(g''(x) = -\frac{1}{x^2} < 0\) pour tout \(x > 0\), la fonction \(\ln(x)\) est concave sur \(]0; +\infty[\).
4. Caractérisation par les tangentes
Une autre façon de voir la convexité : Au lieu de comparer avec les sécantes, on peut comparer la courbe avec ses tangentes.
Théorème 2. (Position par rapport aux tangentes)
Soit \(f\) une fonction dérivable sur un intervalle \(I\).
1. \(f\) est convexe sur \(I\) si et seulement si la courbe de \(f\) est au-dessus de toutes ses tangentes
2. \(f\) est concave sur \(I\) si et seulement si la courbe de \(f\) est en-dessous de toutes ses tangentes
Formulation mathématique : Pour une fonction convexe \(f\) et pour tout \(a \in I\) :
Cette inégalité exprime que la courbe est au-dessus de la tangente en \(a\).
5. Point d'inflexion
Qu'est-ce qu'un changement de convexité ? Quand une fonction passe de convexe à concave (ou inversement), il y a un point particulier où ce changement se produit.
Définition 5. (Point d'inflexion)
Un point d'inflexion est un point de la courbe où celle-ci traverse sa tangente, c'est-à-dire un point où la fonction change de convexité.
Théorème 3. (Condition nécessaire pour un point d'inflexion)
Si \(f\) est deux fois dérivable et si \(x_0\) est l'abscisse d'un point d'inflexion, alors \(f''(x_0) = 0\).
Attention : La réciproque n'est pas vraie ! Il faut vérifier que \(f''\) change effectivement de signe.
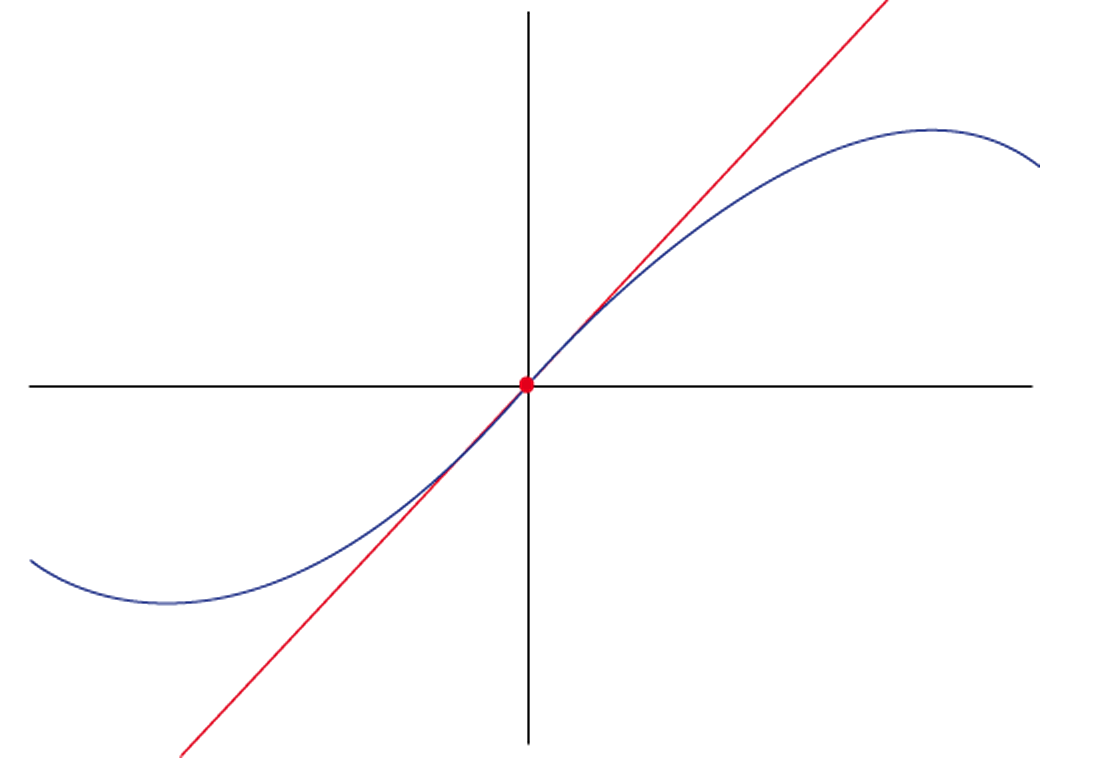
Figure 2. Point d'inflexion : la courbe traverse sa tangente
Exemple 3.
Étudions les points d'inflexion de \(h(x) = x^3\).
\(h'(x) = 3x^2\) et \(h''(x) = 6x\)
\(h''(x) = 0 \Leftrightarrow x = 0\)
Étude du signe de \(h''(x) = 6x\) :
1. Si \(x < 0\) : \(h''(x) < 0\) donc \(h\) est concave
2. Si \(x > 0\) : \(h''(x) > 0\) donc \(h\) est convexe
La fonction change de convexité en \(x = 0\), donc le point \((0, 0)\) est un point d'inflexion.
6. Fonctions de référence
Pourquoi connaître ces résultats ? Ces fonctions apparaissent régulièrement dans les exercices. Connaître leur convexité permet de résoudre plus rapidement les problèmes.
Théorème 4. (Convexité des fonctions usuelles)
1. \(f(x) = x^2\) : convexe sur \(\mathbb{R}\)
2. \(f(x) = x^3\) : concave sur \(]-\infty; 0]\) et convexe sur \([0; +\infty[\)
3. \(f(x) = e^x\) : convexe sur \(\mathbb{R}\)
4. \(f(x) = \ln(x)\) : concave sur \(]0; +\infty[\)
5. \(f(x) = \sqrt{x}\) : concave sur \([0; +\infty[\)
7. Applications de la convexité
À quoi sert la convexité ? La convexité permet de démontrer des inégalités importantes et de résoudre des problèmes d'optimisation.
Exemple d'application : Inégalité arithmético-géométrique (cas \(n=2\))
En utilisant la concavité de \(\ln\) sur \(]0; +\infty[\), on peut démontrer que pour tous \(a, b > 0\) :
Cette inégalité exprime que la moyenne arithmétique est toujours supérieure à la moyenne géométrique.