Terminale : Étude d'un système thermodynamique
📚 Table des matières
1. Introduction
Dans ce chapitre, l'objectif est d'aller plus loin que l'étude mécanique. En effet, cette dernière étudie les interactions entre un système et son environnement. Or, si les systèmes considérés ne sont plus de simples points matériels, alors on observe une variation interne du système.
La thermodynamique se base sur l'étude des transferts thermiques et les conversions d'énergies au sein du système. Pour cela, il est nécessaire de considérer des systèmes avec un grand nombre de molécules.
1.1. Échelle mésoscopique
En thermodynamique, l'échelle microscopique n'est pas adapté puisque les systèmes considérés sont bien trop grand. Par exemple, une simple goutte d'eau possède environ \(10^{22}\) molécules. Appliquer les équations de Newton et les résoudre devient dès lors impossible (il faudrait résoudre \(10^{22}\) équations). Dès lors, on introduit une nouvelle échelle : l'échelle mésoscopique. À cette échelle, seules les grandeurs moyennes (comme la pression, la température etc) ont une importance, sans nécessairement prendre en compte le comportement individuel de chaque molécule.
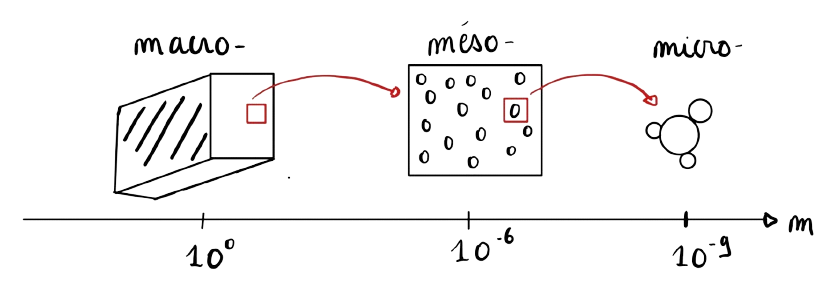
Fig 1. Représentation des différentes échelles
1.2. Système thermodynamique
Après avoir caractérisé l'échelle utilisée, il faut désormais déterminer le système étudié. Un système thermodynamique est une portion de l'espace séparé du reste de l'univers par une frontière. On distingue plusieurs catégories de systèmes :
Différents systèmes thermodynamiques.
1. Système isolé : Système qui n'échange ni énergie, ni matière avec l'extérieur.
Exemple : Le seul véritable système isolé est l'univers lui-même.
2. Système fermé : Système qui n'échange pas de matière mais seulement de l'énergie.
Exemple : Une pompe à chaleur (fournit de l'énergie thermique à une pièce)
3. Système ouvert : Système qui échange de la matière et de l'énergie avec l'extérieur.
Exemple : Une centrale nucléaire.
Dans le cadre de ce chapitre, seuls les systèmes dit fermés seront étudiés.
2. Étude d'un système thermodynamique
Une fois le système bien défini, l'étude thermodynamique permet d'étudier la variation d'énergie au sein même du système lors de son évolution. Pour cela, il nous faut étudier l'énergie interne d'un système.
2.1. Énergie interne
En mécanique classique, un système possède une énergie cinétique et une énergie potentielle macroscopique. Néanmoins, chaque molécule constituant le système possède une énergie (ex : agitation). Si l'on veut rendre compte de l'énergie interne d'un système, il faut considérer ses énergies microscopiques. On note \(E_{c,micro}\) et \(E_{p,micro}\) respectivement l'énergie cinétique et l'énergie potentielle microscopique globale du système thermodynamique :
Énergie interne.
L'énergie interne U d'un système thermodynamique vaut : \[ U = E_{c,micro} + E_{p,micro} \]
2.2. Variables d'état
Pour décrire un tel système, on utilise un petit nombre de variables permettant de décrire complètement son état macroscopique.
Exemple.
Les variables d'états utilisées en règle générale sont la pression P, la température T ou encore la masse volumique \(\rho\).
2.3. Transformations thermodynamiques (Hors-programme)
On s'intéresse désormais aux transformations internes que peut subir un système thermodynamique. Pour cela, on en distingue différents types ;
Différents types de transformations thermodynamiques.
1. Transformation isobare : Transformation à pression constante du système.
2. Transformation isochore : Transformation à volume constant du système.
3. Transformation isotherme : Transformation à température constante du système.
3. Premier principe de la thermodynamique
3.1. Énoncé du premier principe
Après avoir caractérisé complètement un système thermodynamique, étudier l'évolution de l'énergie interne d'un système au cours du temps est nécessaire. Pour cela, on introduit le premier principe de la thermodynamique :
Premier principe de la thermodynamique.
Pour un système thermodynamique fermé, l'énergie interne du système U vérifie la relation suivante :
Remarque : \(Q\) et \(W\) sont des grandeurs algébriques (peuvent être négatifs où positifs) :
1. Si \(Q>0\), alors le système reçoit effectivement de l'énergie thermique à l'extérieur. (De même, si \(W>0\), le système reçoit effectivement du travail)
2. Si \(Q<0\), alors le système cède de l'énergie thermique à l'extérieur. (De même, si \(W<0\), le système fournit du travail vers l'extérieur)
3.2. Cas particulier d'un système incompressible
Lorsque le système considéré est incompressible (= le volume du système reste constant), c'est le cas par exemple d'une bouteille remplie d'air avec le bouchon fermé, alors il existe, lors d'une transformation, une relation entre la variation de température \(\Delta T = T_{final} - T_{initial}\) et la variation d'énergie interne \(\Delta U= U_{final} - U_{initial}\).
Système incompressible.
Lors d'une transformation pour un système incompressible, \(\Delta U\) est proportionnel à \(\Delta T\) et vérifie : \[ \Delta U = C \Delta T \] où \(C\) représente la capacité thermique (en J.K⁻¹) et est souvent exprimé sous la forme : \(C = m \times c\), où m est la masse du système (en kg) et c est la capacité thermique massique (en J.K⁻¹.kg⁻¹)
3.3. Un exemple concret
Considérons un système fermé et incompressible rempli d'eau de masse \(m = 1,5\) kg et de capacité thermique massique \(c = 4180\) J.K⁻¹.kg⁻¹. À l'état initial, le système est à une température \(T_0 = 10°C\). Ce système reçoit une énergie thermique via une résistance de \(R = 50 \Omega\) parcouru par une intensité \(I = 20 A\). Au bout de combien de temps l'eau commencera-t-elle à bouillir ?
On rappelle que la puissance dissipée par effet joule à pour expression : \(P_{th} = R I^2\)
Correction
Appliquons le premier principe de la thermodynamique au système rempli d'eau. Il n'y a pas de travail en jeu et on note Q le transfert thermique reçu par le système. Alors : \[ \Delta U = Q + 0 \] Or, on sait que la puissance dissipée par effet joule \(P_{th}\) correspond à l'énergie thermique reçu par le système (\(Q\)) durant un temps \(\Delta t\), correspondant à l'instant où l'eau se met à bouillir. Donc : \[ \text{(i)} \hspace{10pt} Q = P_{th} \Delta t = R I^2 \Delta t \] D'autre part, le système est incompressible, donc en utilisant le résultat de la section précédente : \[ \text{(ii)} \hspace{10pt} \Delta U = m c (T_{final} - T_{initial}) \] Or, la température finale correspond à l'instant où l'eau se met en ébullition : \(T_{\text{final}} = 100\,^{\circ}\mathrm{C}\). Finalement, en utilisant les résultats \textit{(i)}, \textit{(ii)} et le premier principe, on obtient : \[ \Delta t = \frac{m c (T_{final} - T_{initial})}{R I^2} \] L'application numérique donne : \(\boxed{\Delta t \approx 28 \text{ s}}\)
Remarque : Nous n'avons pas eu besoin de convertir les unités de température en Kelvin car nous avons fait une différence de deux températures.