Terminale : La lumière comme un flux de particules
📚 Table des matières
1. L'effet photoélectrique ou la naissance du photon
1.1. L'effet photoélectrique
L'effet photoélectrique a été découvert par Heinrich Hertz en 1887. Lors de ses expériences sur les ondes électromagnétiques, Hertz a remarqué un phénomène inattendu : lorsqu'il exposait des surfaces métalliques à de la lumière ultraviolette, elles émettaient des électrons. Cette observation était cruciale car elle démontrait que la lumière pouvait directement provoquer l'émission d'électrons d'une surface métallique, un effet désormais connu sous le nom d'effet photoélectrique.
En 1905, Albert Einstein a proposé une explication révolutionnaire de l'effet photoélectrique, qui allait au-delà des théories classiques de l'époque. Einstein a postulé que la lumière n'était pas simplement une onde continue, comme on le croyait à l'époque, mais qu'elle était composée de quanta discrets d'énergie, appelés photons (photon = paquet d'énergie). Selon Einstein, chaque photon avait une énergie \(E\) proportionnelle à la fréquence de la lumière par la relation fondamentale suivante :
1.2. Le modèle de photon
Définition 1. (La constante de Planck)
La constante de Planck est une des constantes fondamentales de l'univers, notée traditionnellement \(h\), et valant \(6,63.10^{-34}\) J.s.
Remarque : Dans certains textes, nous pouvons retrouver la notation \(\hbar\). Cette dernière est appelée constante de Planck réduite et est définie comme suit : \[ \hbar=\frac{h}{2\pi} \]
Définition 2. (Le photon)
Le photon est une particule élémentaire sans masse, constituant la lumière, se déplaçant à la même vitesse que la lumière, ayant une énergie \(E\) et une impulsion \(p\) définies par :
La première relation est appelée relation de Planck-Einstein (allemands), la seconde est appelée la relation de De Broglie (français).
Exercice 1.
Montrer la relation suivante entre l'énergie \(E\) et l'impulsion \(p\) d'un photon dans le vide : \[ \boxed{E=pc} \] où \(c\) est la vitesse de la lumière dans le vide.
1.3. Le seuil d'extraction
Le seuil d'extraction est défini par l'énergie minimale qu'il faut apporter pour que les électrons soient arrachés par la lumière à la surface d'un métal : c'est le travail d'extraction.
Définition 3. (Le travail d'extraction)
Le travail d'extraction est l'énergie minimale qu'il faut apporter aux électrons situés à la surface d'un métal pour les arracher de la surface. Généralement, on note \(W_e\) ce travail d'extraction et il diffère en fonction du métal considéré.
Ainsi, pour décrire l'effet photoélectrique, il faut tenir compte de cette énergie minimale qu'il faut que les photons incidents (arrivant sur le métal) aient pour décrire leur énergie \(E\) après avoir arraché les électrons de la surface du métal. Ainsi, les photons qui auront arrachés des électrons à la surface du métal auront une énergie \(E\) égale à :
Interprétation : Si les photons n'ont pas une énergie \(hf \le W_e\) alors aucun électron ne sera arraché, en revanche, si leur énergie initiale \(hf \ge W_e\) alors des électrons sont arrachés et leur énergie finale vaut \(E=hf-W_e\).
2. La quantification de l'infiniment petit avec le modèle de Bohr
Au début du 20ème siècle, Niels Bohr, physicien danois, publie une série d'ouvrages présentant un nouveau modèle de l'atome. L'atome serait composé en son centre d'un noyau composé de protons et de neutrons (formant les nucléons) et d'électrons qui gravitent autour de l'atome sur des orbites accessibles à différents niveaux d'énergies.
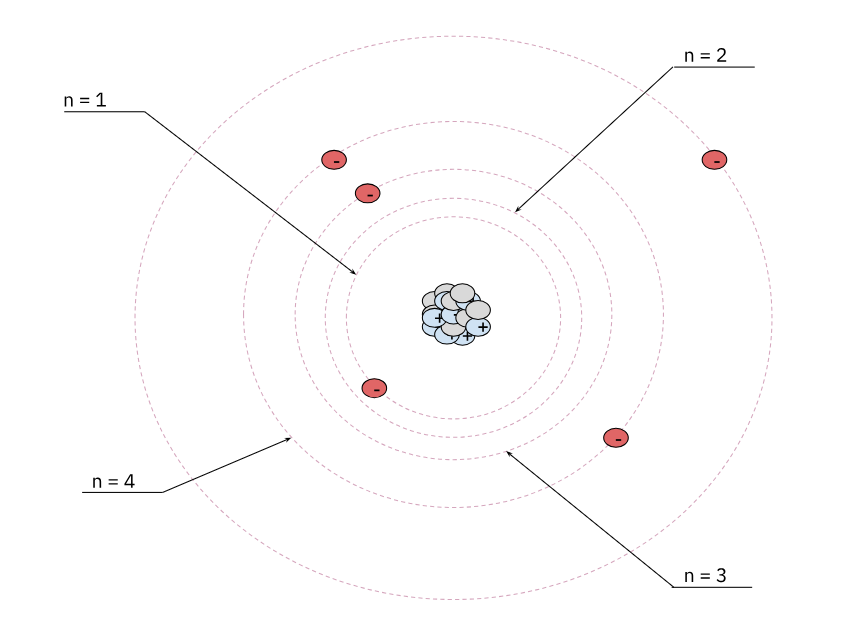
Figure 1. Représentation d'un atome léger (\(Z \lt 10\)) selon le modèle de Bohr
La figure 1 représente un atome léger, ayant un nombre atomique \(Z\) faible, les éléments gris représentant les neutrons, les éléments bleus les protons et les éléments rouges les électrons. On voit bien que les électrons sont situés que sur des orbites, appelées orbites électroniques. Chaque orbite est numéroté par un entier \(n \ge 1\).
2.1. La quantification de l'énergie d'un atome
Dans la théorie de Bohr, les niveaux d'énergies capables d'être atteints par un électron définissent l'état de l'électron (son numéro d'orbite associé).
L'atome d'hydrogène possède plusieurs niveaux d'énergie : le premier niveau, appelé état fondamental où les électrons qui y sont ont une énergie égale à \(E_0=-13,6\) eV ; les autres niveaux ont une énergie définie par la relation suivante :
Rappel : En physique atomistique, on définit l'électron-volt, noté 1 eV, comme l'énergie d'un électron lorsqu'il traverse, d'une armature à l'autre, un condensateur alimenté sous 1 Volt . Ainsi, on en déduit que :
2.2. La quantification des rayons des orbites électroniques
Comme l'énergie est discrétisée alors les rayons des orbites aussi. Si l'on note \(r_n\) la rayon du n-ème état (de la n-ème orbite) alors on en déduit la relation suivante : \[ r_n=n^2a_0 \] où \(a_0\) est appelé le rayon de Bohr valant 53 pm (1 pm = \(10^{-12}\) m).
Exercice 2.
Expliquer en quoi la représentation de l'atome en figure 1 est conforme à la théorie de Bohr.
2.3. Lien à la cellule photovoltaïque
2.3.1. Principe de fonctionnement
Une cellule photovoltaïque, ou cellule photoélectrique est un composant électronique qui, exposé à la lumière, produit de l’électricité grâce à l’effet photoélectrique.
En effet, lorsqu'une surface conductrice est exposée à un flux de photons (lumière) alors si l'énergie du flux est suffisante, ce dernier vient arracher à la plaque conductrice quelques électrons. Cela créé des trous et pour les combler, des électrons artificiellement ajoutés viennent les boucher. Ainsi, on créé une mise en mouvement d'électrons à l'origine du courant électrique.
2.3.2. Puissance électrique fournie
La cellule photovoltaïque assure une conversion photoélectrique (lumière en électricité). A l'état initial, le flux de photons incident a une puissance, appelée puissance fournie et notée \(P_{fournie}\) définie par : \[ P_{fournie}=hf\Delta t \] où \(f\) est la fréquence du flux et \(\Delta t\) la durée d'exposition.
En sortie de la cellule photovoltaïque, l'utilisateur récupère une puissance utile notée \(P_{utile}\). On définit alors le rendement comme une mesure de qualité sur la conversion réalisée, autrement dit, le rendement mesure à quel point notre converser est satisfaisante. En notant \(\eta\) ce rendement, on peut alors l'écrire comme : \[ \eta=\frac{P_{utile}}{P_{fournie}} \]
2.3.3. Calcul du rendement
Pour déterminer la puissance utile, nous avons besoin de la courbe \((I,U)\), on parle de courbe caractéristique de la cellule photovoltaïque. Cette courbe représente en ordonnée l'intensité à travers la cellule en fonction de la tension à ses bornes.
A partir de la courbe \((I,U)\), on détermine la puissance utile par la relation suivante : \[ P_{utile}=U\times I \] On peut même obtenir la courbe de la puissance en prenant différentes valeurs de points \((I,U)\) afin d'obtenir par exemple la puissance utile maximale afin de déterminer le rendement maximal possible à avoir. Finalement, on montre que :