Terminale : La lunette astronomique
Ce cours s'intéresse à un système optique dont l'utilisation est très prisée lorsqu'il s'agit d'observer des objets lointains avec une bonne résolution : la lunette afocale de Kepler appelée aussi la lunette astronomique. Cette lunette est composée de deux lentilles minces convergentes bien placées de façon à ce que l'image de tout objet provenant de l'infini soit observable à l'œil nu.
📚 Table des matières
1. Définitions
Définition 1. (Source de lumière)
On différencie deux sources de lumières : les sources primaires et secondaires. Les sources de lumière primaires sont celles qui émettent leur propre lumière. Les sources de lumières secondaires sont celles qui émettent de de la lumière par réflexion ou encore par diffraction.
Par exemple, le Soleil produit sa propre lumière : c'est une source de lumière primaire. En revanche, la Lune renvoie de la lumière grâce à la réflexion de la lumière provenant du Soleil sur sa surface : c'est une source de lumière secondaire.
On retiendra pour la suite alors que tout objet émet de la lumière lorsqu'il est éclairé s'il n'est pas une source primaire de lumière.
Définition 2. (De l'infini)
On dit d'un objet qu'il est à l'infini lorsqu'il est à une distance de la première lentille très grande devant sa distance focale. Si l'on note \(D\) la distance entre la lentille et l'objet, \(f'\) la distance focale de la lentille alors on dit que l'objet est situé à l'infini par rapport à cette lentille lorsque :
Lorsque l'objet étudié est à une distance de 1 mètre par rapport à une lentille de distance focale \(f'=1\) cm alors on peut considérer que l'objet est à l'infini. Finalement, avec les notations précédentes, si \(\boxed{D>10f'}\), on pourra faire l'hypothèse de l'objet situé à l'infini.
Propriété 1. (Rayon provenant de l'infini)
Un rayon lumineux provenant d'un objet situé à l'infini est un rayon qui provient de l'infini. Tous les rayons provenant de l'infini sont parallèles entre eux.
Preuve
Il suffit de faire un tracé dans le cas d'un objet situé à l'infini. D'un point de vue géométrique, on peut considérer que ces rayons sont de plus en plus parallèles entre eux lorsque l'objet est plus éloigné.
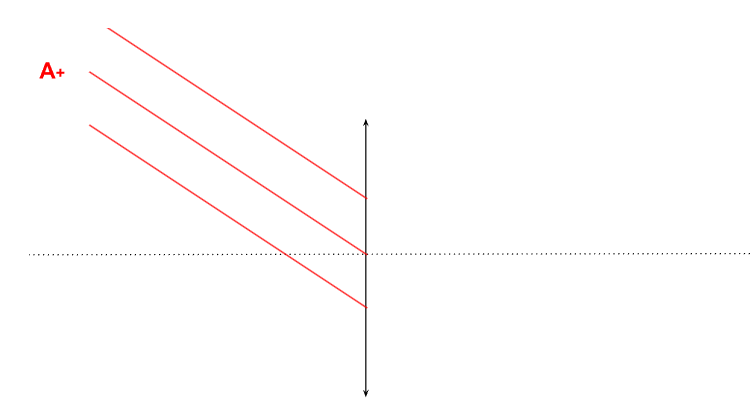
Figure 1. Représentation des rayons provenant de l'infini d'un objet \(A_+\) situé à l'infini
Remarque : Cette propriété est observée lorsqu'on étudie les rayons lumineux qui proviennent du Soleil. Lorsqu'on s'intéresse à la méthode d'Ératosthène pour obtenir une première approximation du rayon de la Terre, on fait l'hypothèse, presque vraie, que les rayons provenant du Soleil sont parallèles entre eux.
Propriété 2. (Image d'un objet à l'infini par une lentille mince convergente)
L'image d'un objet situé à l'infini par une lentille mince convergente est situé sur le plan focal image de cette lentille.
Propriété 3. (Image d'un objet situé sur le plan focal objet par une lentille mince convergente)
L'image d'un objet situé sur le plan focal objet d'une lentille mince convergente est situé à l'infini.
Ces deux dernières propriétés seront utilisées pour définir la lunette astronomique.
2. La lunette astronomique
2.1. Introduction à la lunette afocale
Définition 3. (Système optique afocal)
On dit d'un système optique qu'il est afocal lorsqu'il renvoie une image située à l'infini d'un objet situé à l'infini.
Dès à présent, nous ferons l'étude que des système optiques à deux lentilles minces convergente en série (c'est-à-dire posées à la suite sur l'axe optique).
Propriété 4. (Conjugaison des foyers)
Dans le cas d'un système afocal à deux lentilles minces convergentes, le foyer image de sa première lentille coïncide exactement avec le foyer objet de sa seconde lentille.
Preuve
C'est une conséquence de la définition 3. Si l'on veut que l'image obtenue par la seconde lentille soit à l'infini, l'objet « intermédiaire » doit être situé sur le plan focal objet de cette seconde lentille d'après la propriété 3. Or la première lentille forme l'image de tout objet situé à l'infini sur son plan focal image d'après la propriété 2. Si ces deux plans coïncident, on forme bien un système afocal.
2.2. Construction de la lunette astronomique
Définition 4. (Lunette astronomique)
La lunette astronomique est un système optique afocal à deux lentilles minces convergente en série.
On parle aussi de lunette afocale de Kepler ou encore simplement lunette de Kepler.
Méthode 1. Construction de la lunette astronomique (à savoir)
La lunette astronomique est composée de deux lentilles minces convergentes en série formant un système optique afocal d'après la définition 4. Si l'on note \(f_1\) et \(f_2\) la distance focale respectives de la première lentille appelée objectif et de la seconde lentille appelée oculaire. La propriété 4 impose :
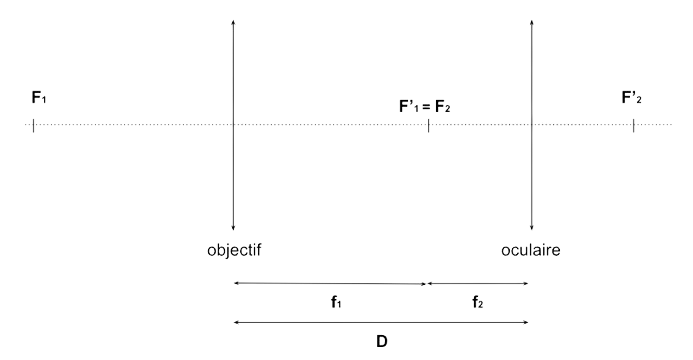
Figure 2. Représentation de la lunette astronomique
Maintenant l'objectif est d'étudier comment sont déviés les rayons provenant de l'infini par un objet situé à l'infini à travers la lunette astronomique pour obtenir à la sortie, des rayons à l'infini.
Méthode 2. Devenir des rayons lumineux à travers la lunette astronomique (à savoir)
Avec ce que l'on sait, construisons le devenir des rayons lumineux à travers cette lunette. D'abord, nous n'avons besoin que d'un seul rayon lumineux au départ pour faire nos tracés mais pour un souci de compréhension, on en prendra deux car on dit toujours en optique qu'il suffit d'au moins deux rayons pour obtenir l'image d'un objet par une lentille.
Soient \((1)\) et \((2)\) deux rayons à l'infini qui arrivent sur l'objectif, comme ils proviennent de l'infini, la proposition 2 permet de dire qu'ils se coupent sur le plan focal image de l'objectif. On détermine ce point à l'aide du rayon qui passe par le centre optique de l'objectif et qui n'est jamais dévié :
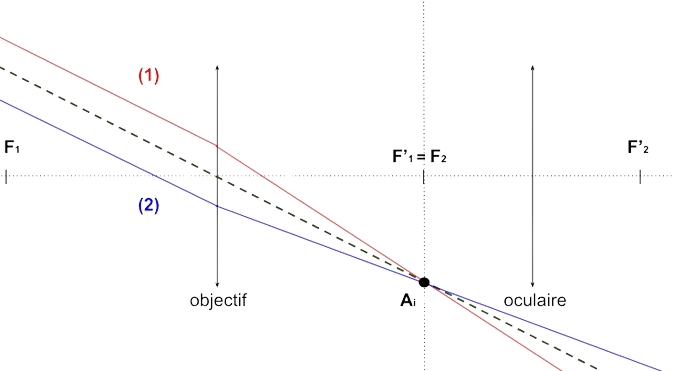
Figure 3. Image formée par l'objectif
Ainsi, on a récupéré le point intermédiaire qu'on a noté \(A_i\). Avec ce point, nous allons construire son image par la seconde lentille, l'oculaire, ce qui nous permettra de conclure.
Comme \(A_i\) ce situe sur le plan focal objet de l'oculaire, son image par l'oculaire sera à l'infini d'après la proposition 3 : en toute rigueur, on devrait considérer l'image intermédiaire \(F'_1A_i\) équivalent aussi à \(F_2A_i\). Ainsi, on a :
.png)
Figure 4. Image formée par l'oculaire
En effet, en considérant à nouveau le rayon passant par le centre optique de l'oculaire alors comme il n'est jamais dévié, alors il donne la direction des rayons émergeant parallèles entre eux. Dès lors, pour construire les rayons en sortie, il faut construire les parallèles du rayon qui passe par le centre optique de l'oculaire.
Conclusion : comme convenu, les rayons à l'infini en entrée ressortent, à travers la lunette astronomique, parallèles entre eux en sortie.
Maintenant, introduisons les angles \(a\) et \(a'\) qui définissent respectivement l'angle apparent des rayons (1) ou (2) (c'est le même) et l'angle apparent des rayons en sortie (en orange sur la figure 3). Ces angles vont nous permettre de caractériser le grossissement notée \(G\) de la lunette astronomique : c'est normal, ce dispositif permet de voir en plus « gros » les objets situés à l'infini.
Remarque : On utilise la lunette de Kepler pour observer les objets célestes : la Lune par exemple. Attention, on ne l'utilise pas sans protection pour observer le Soleil car la lunette concentre sur l'oculaire toute la luminosité perçue en entrée en un point de petite dimension ce qui peut brûler la rétine. On peut remarquer que la lunette astronomique augmente la luminosité de l'objet observé en plus de sa taille.
Définition 5. (Grossissement)
Le grossissement d'une lunette astronomique notée \(G\) est définit comme :
Comme dit précédemment, ce dernier mesure à quel point la lunette grossit les objets observés.
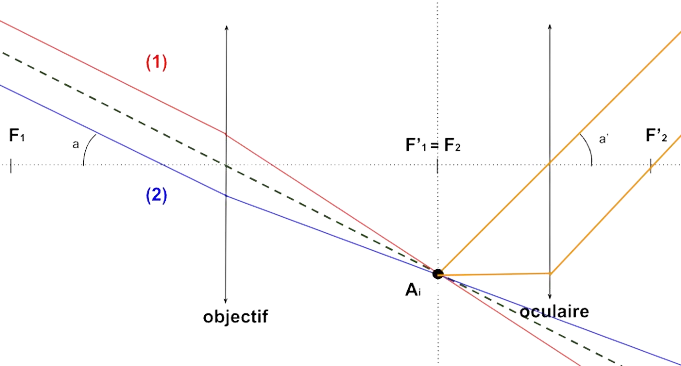
Figure 5. Position des angles \(a\) et \(a'\)
Un résultat à connaître et à savoir démontrer est l'expression du grossissement \(G\) en fonction des distances focales de l'objectif et de l'oculaire. C'est le résultat qui suit :
Proposition 1. (Grossissement)
Si l'on note \(f_1\) la distance focale de l'objectif, \(f_2\) la distance focale de l'oculaire et \(G\) le grossissement de la lunette astronomique alors :
Preuve
En observant la figure, on remarque d'après les formules trigonométriques et en utilisant les propriétés des angles alternes internes : \[ \tan(a)=\frac{F'_1A_i}{f_1} \quad \textrm{et} \quad \tan(a')=\frac{F_2A_i}{f_2} \] Dans l'approximation de Gauss des petits angles (on suppose que les rayons incidents sont peu inclinés par rapport à l'axe optique) : \[ \tan(a)\approx a \quad \textrm{et} \quad \tan(a')\approx a' \] On en déduit alors : \[ G=\frac{a'}{a}=\frac{\frac{F_2A_i}{f_2}}{\frac{F'_1A_i}{f_1}}=\frac{f_1}{f_2} \] ce qui achève cette preuve à connaître.