Terminale : Les lentilles minces
Les lentilles minces sont des dispositifs optiques fascinants qui jouent un rôle crucial dans de nombreux domaines, de la conception d'appareils optiques à la vision humaine elle-même. Comprendre le fonctionnement des lentilles minces est essentiel pour une variété d'applications, allant de l'ingénierie optique à la conception de lunettes correctrices et de lentilles de contact.
Nous allons étudier le comportement de la lumière à travers les lentilles minces et comment se forme l'image d'un objet à travers ces dernières. Pour compléter ce cours, nous vous invitons à aller consulter le cours sur le comportement géométrique de la lumière.
📚 Table des matières
1. Postulats sur la lumière
Définition 1. (Milieu homogène)
Un milieu est homogène lorsque ses propriétés physiques sont identiques en tout point.
La densité et l'indice de réfraction (cf. cours sur le comportement géométrique de la lumière) sont des exemples de propriétés physiques.
Définition 2. (Milieu isotrope)
Un milieu est isotrope lorsque suivant toutes les directions de propagation de la lumière, ses propriétés physiques sont identiques.
Remarque : Ces notions de milieu homogène et isotrope ont été vues dans le cours sur la dynamique du point matériel. En mécanique, un milieu homogène permet d'établir la conservation de la quantité de mouvement et un milieu isotrope permet d'établir la conservation du moment cinétique (capacité d'un système à à être en rotation sur lui-même).
En optique géométrique, nous pouvons représenter les rayons lumineux avec des tracés (traits). Cette représentation est idéaliste, elle ne représente pas la réalité. En effet, Einstein a postulé que la lumière est composée de particules qu'on appelle photons. Les photons sont des particules qui n'ont pas de masse et qui n'agissent pas avec leur environnement, à priori ils n'ont pas de volume. Les rayons lumineux obéissent à trois postulats indispensables si l'on veut faire de l'optique géométrique.
Postulat 1. (Géométrie des rayons lumineux)
Dans un milieu homogène et isotrope, les rayons lumineux sont des droites.
Postulat 2. (Loi du retour inverse de la lumière)
Le trajet effectué par la lumière pour aller d'un point à un autre est le même qu'elle emprunte pour faire le trajet inverse.
Ce postulat découle d'un principe variationnel, on parle aussi de principe de Fermat. Un principe variationnel est un principe selon lequel une grandeur est minimisée par rapport à d'autres grandeurs et vérifiant certaines contraintes. Ce que l'on minimise, c'est le temps de parcours de la lumière.
Postulat 3. (Les rayons lumineux sont indépendants)
Il n’y a pas d’interaction entre deux rayons lumineux, un rayon ne peut pas donc en dévier un autre.
2. Introduction aux lentilles minces
Définition 3. (Une lentille)
Une lentille est un milieu transparent délimité par deux dioptres.
En général, les dioptres ont des formes classiques : plans ou sphériques. Dans le cadre du programme, on suppose que les deux dioptres sont quasiment confondus et qu'ils sont plans.
Définition 4. (Une lentille mince)
Une lentille est mince lorsque sa hauteur est très grande devant son épaisseur.
Si l'on note \(h\) la hauteur de la lentille et \(e\) son épaisseur. On dit que la lentille est mince lorsque \(\boxed{h \gg e}\).
Définition 5. (Centre optique)
On appelle centre optique d'une lentille mince, le point situé sur l'axe optique par lequel tout rayon lumineux n'est pas dévié.
Cette définition est conforme au programme MAIS elle n'est pas rigoureusement bien écrite. La formulation qui suit est hors-programme. En effet, comme une lentille mince n'est pas d'épaisseur nulle, un rayon lumineux passant par son centre optique est nécessairement dévié. Cette déviation rend le rayon sortant parallèle au rayon fictif obtenu par prolongement du rayon incident.
Définition 6. (Lentille mince convergente)
Une lentille mince est convergente lorsque les rayons incidents qui en ressortent convergent vers l'intérieur.
Les lentilles minces convergentes sont celles qui sont les plus étudiées au programme de terminale.
Définition 7. (Lentille mince divergente)
Une lentille mince est divergente lorsque les rayons incidents qui en ressortent divergent vers l'extérieur.
Définition 8. (Foyer objet d'une lentille mince convergente)
Le foyer objet d'une lentille mince convergente est l'unique point par lequel un rayon incident qui passe par lui émerge parallèlement à l'axe optique en sortie. Il est situé à gauche de la lentille à une distance \(f'\), appelée distance focale.
Définition 9. (Foyer image d'une lentille mince convergente)
Le foyer image d'une lentille mince convergente est l'unique point par lequel un rayon sortant de la lentille qui passe par lui avait son rayon incident parallèle à l'axe optique. Il est situé à droite de la lentille à une distance \(f'\), appelée distance focale.
Remarque : On a des définitions analogues pour la lentille mince divergente sauf que le foyer objet de la lentille mince divergente correspond au foyer image de la lentille mince convergente et le foyer image de la lentille mince divergente correspond au foyer objet de la lentille mince convergente.
3. Représentation des lentilles minces
On peut représenter schématiquement les lentilles minces convergentes et divergentes.
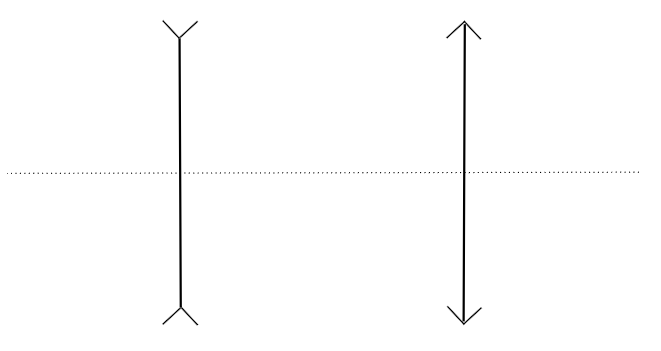
Figure 1. Représentation des lentilles, à gauche la lentille
divergente, à droite, la lentille convergente
Sur la figure 1, l'axe en pointillé désigne l'axe optique. L'intersection entre les lentilles et l'axe optique définit le centre optique. On le note couramment \(O\).
Notons \(F\) et \(F'\) les foyers objet et image respectivement. La lentille mince convergente s'écrit :
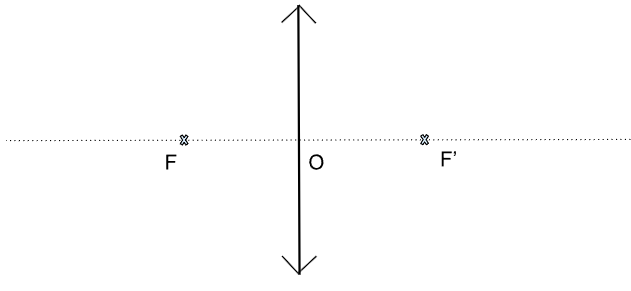
Figure 2. Lentille mince convergente
Sur le dessin, les caractéristiques de la lentille mince convergente permettent d'établir : \[ \overline{OF}=\overline{OF'}=f' \] où \(f'\) est la distance focale.
On réalise la même chose avec la lentille divergente en respectant les définitions :
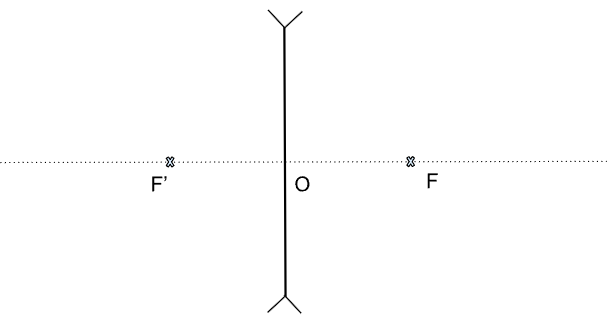
Figure 3. Lentille mince divergente
Définition 10. (La vergence)
On définit la vergence comme l'inverse de la distance \(\overline{OF}=\overline{OF'}\) notée \(V\) définie comme suit :
En général, \(n=1\) car on étudie la propagation des rayons lumineux à travers les lentilles dans l'air ou le vide.
Remarque : La notation \(\overline{OF}\) désigne la distance algébrique de norme \(OF\). Si l'on suppose que l'axe optique est orienté vers la droite alors, \(\overline{OF}=-OF<0\) mais \(\overline{OF'}=OF'>0\) dans le cas d'une lentille mince convergente.
4. Construction d'une image à travers une lentille
4.1. Premiers résultats
On considère un objet noté \(AB\) sur le dessin dont on veut déterminer l'image à travers une lentille mince convergente dans le cas où \(\overline{OA}\). Il ne suffit que de deux rayons pour construire l'image notée \(A'B'\) mais on part du postulat qu'il en faut trois, le troisième étant le rayon qui vérifie qu'on a bien construit \(A'B'\).
On suppose d'abord que \(|\overline{OA}|>|\overline{OF}|\).
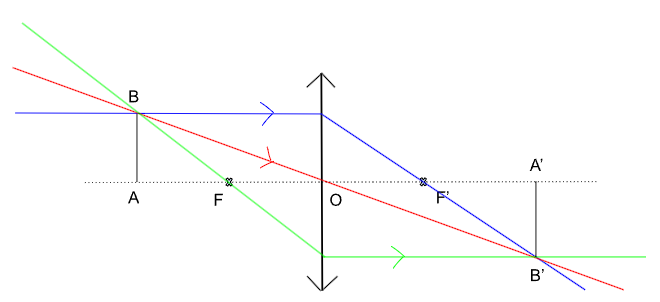
Figure 4. Image formée par une lentille mince convergente, \(|\overline{OA}|>|\overline{OF}|\)
Maintenant, nous pouvons définir plusieurs relations vérifiées pour une lentille mince.
Proposition 1. (L'agrandissement)
On définit comme étant l'agrandissement, la grandeur notée \(\gamma\) qui donne le rapport d'agrandissement entre la taille de l'image et la taille de l'objet à travers une lentille mince. On la définit comme suit :
La première égalité est une définition. La seconde se démontre à partir du théorème de Thalès. Attention, on préfère parler d'agrandissement longitudinal si l'on veut être rigoureux noté \(\gamma_l\). On peut aussi parler d'agrandissement transversal noté \(\gamma_t\).
Proposition 2. (La relation de Newton)
Toute lentille mince vérifie la relation suivante, appelée relation de Newton :
Cette relation se démontre à partir de la proposition 1 et du théorème de Thalès.
Proposition 3. (La formule de conjugaison)
Toute lentille mince vérifie la formule de conjugaison, appelée aussi relation de Descartes :
Preuve (HP)
En utilisant la relation de Chasles dans la relation de Newton en \(O\), on a : \[ (\overline{F'O}+\overline{OA'} )\times(\overline{FO}+\overline{OA} )=-f'^2 \iff (-f'+\overline{OA'} )\times(f'+\overline{OA} )=-f'^2 \] car \(\overline{F'O}=-f'\) (sens indirect) et \(\overline{FO}=f'\) (sens direct). En simplifiant, il en suit que : \[ f'\overline{OA'}-f'\overline{OA}+\overline{OA}\times\overline{OA'}=0 \] En divisant par \(f'\overline{OA}\times\overline{OA'}\), on en déduit la formule de conjugaison : \[ \boxed{\frac{1}{\overline{OA'}}-\frac{1}{\overline{OA}}=\frac{1}{f'}} \]
4.2. Constructions géométriques
Dans le paragraphe précédent, on introduisait les premiers résultats de l'optique géométrique. Ce sont les résultats qui seront toujours vérifiés en pratique. On pourra les utiliser pour vérifier la justesse de nos schémas.
Remarque : On notera LMC pour lentille mince convergente et LMD pour lentille mince divergente.
Construction 1 - cas où \(|\overline{OA}|>|\overline{OF}|\) (LMC) et \(|\overline{OA}|>|\overline{OF'}|\) (LMD) avec \(A\) à gauche
Pour une lentille mince convergente, voici la construction :

Figure 5. Image réelle et renversée formée d'un objet réel
Pour une lentille mince divergente, voici la construction :
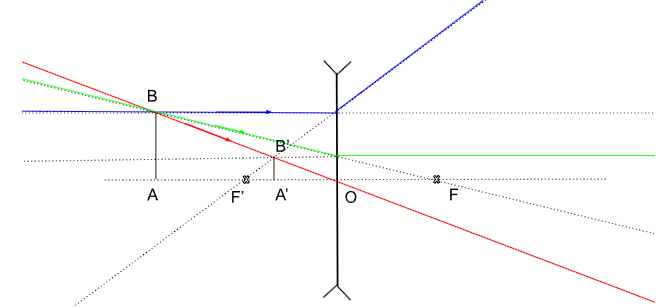
Figure 6. Image virtuelle et droite formée d'un objet réel
Construction 2 - cas où \(|\overline{OA}|<|\overline{OF}|\) avec \(A\) à gauche (LMC) et \(A\) à droite (LMD)
Pour une lentille mince convergente, voici la construction :
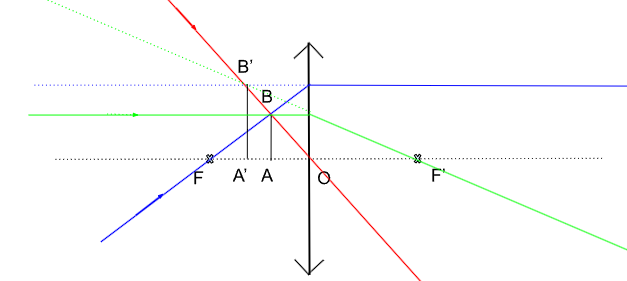
Figure 7. Image virtuelle et droite formée d'un objet réel
Pour une lentille mince divergente, voici la construction :
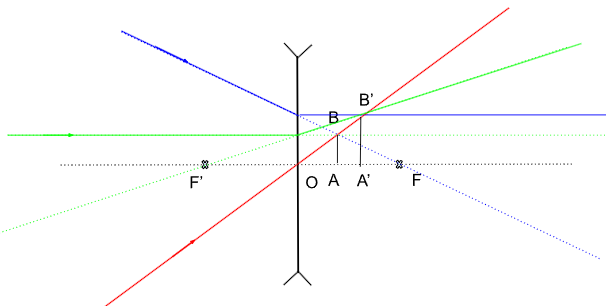
Figure 8. Image réelle et droite formée d'un objet virtuel
Remarque : Les adjectifs de réelle, virtuelle, droite ou renversée sont détaillés dans le cours sur la lunette astronomique. Notons par ailleurs que certaines constructions non mentionnées ici mais très courantes sont présentes dans ce cours dont on vous conseille vivement sa lecture ensuite.
Construction 3 - cas où \(|\overline{OA}|>|\overline{OF'}|\) (LMC) et \(|\overline{OA}|>|\overline{OF}|\) (LMD) avec \(A\) à droite
Pour une lentille mince convergente, voici la construction :
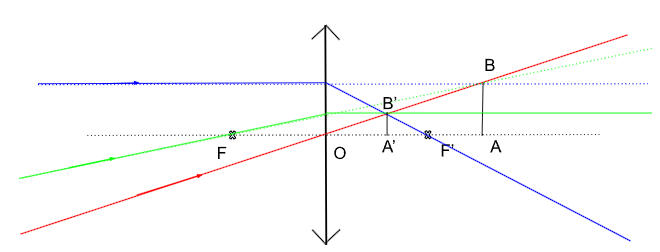
Figure 9. Image réelle et droite formée d'un objet virtuel
Pour une lentille mince divergente, voici la construction :
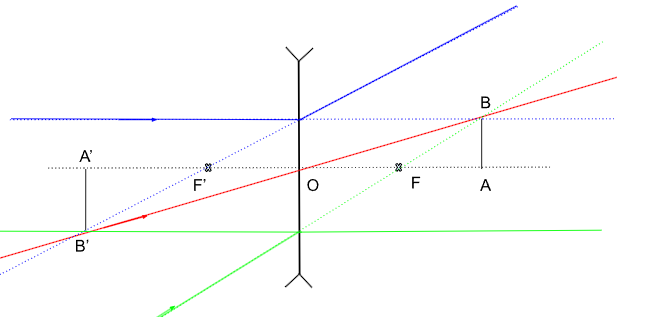
Figure 10. Image virtuelle et renversée formée d'un objet virtuel
Construction 4 - Construction de l'émergent, rayons provenant de l'infini
Pour une lentille mince convergente, voici la construction :
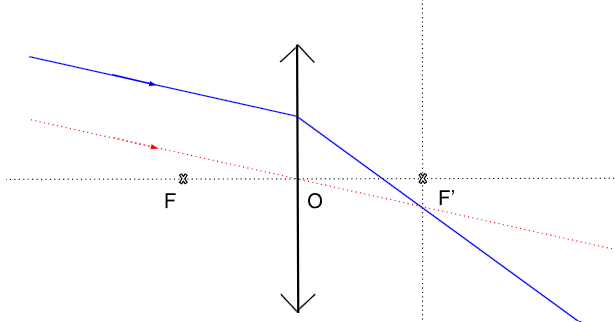
Figure 11. Détermination de la trajectoire du rayon bleu pour une LMC
Pour une lentille mince divergente, voici la construction :
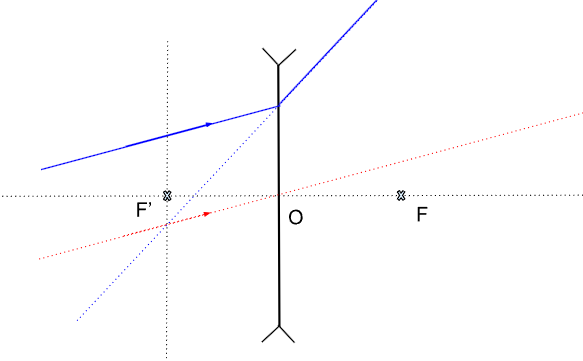
Figure 12. Détermination de la trajectoire du rayon bleu pour une LMD
Remarque : Le principe de la lunette astronomique repose sur la tracé de la figure 11.