Terminale : Exercices sur la mécanique des fluides
La mention ❤️ indique que la méthode de résolution proposée par l'exercice est à maîtriser et à savoir refaire, on peut aussi parler d'exercice classique. Finalement, chaque exercice possède sa propre difficulté : 🌶️ pour un exercice facile, 🌶️🌶️ pour un exercice de difficulté moyenne et 🌶️🌶️🌶️ pour un exercice difficile dans sa résolution.
Exercices d'application
Exercice 1 (Formule de Torricelli) ❤️ 🌶️ 🌶️ 🌶️
Le but de cet exercice est d'établir la formule de Torricelli : on considère un récipient de hauteur \(h\) dont on creuse un trou vertical de section \(S\) dans son fond. La situation se schématise comme suit :
.png)
La vitesse au point \(B\) est donnée alors par la formule de Torricelli : \[ v_B=\sqrt{2gh} \] avec \(g\) l'intensité de pesanteur supposée constante.
Le fluide assimilé à de l'eau est supposé parfait, incompressible et est représenté en bleu. On suppose que son écoulement à travers \(B\) est permanent et on note \(S_B\) la section du trou en \(B\). On suppose initialement que l'altitude de \(A\) vaut \(h\) et qu'au cours du temps, cette dernière diminue (\(h=h(t)\)). On note \(g\) l'intensité de la pesanteur supposée constante dont le vecteur est dirigé vers le bas. On note \(v_A\) la vitesse du point \(A\), \(v_B\) celle du point \(B\) et \(S_A\) la section en \(A\).
1. En utilisant la conservation du débit en \(A\) et en \(B\), établir que : \[ v_B \gg v_A \]
2. En considérant une ligne de courant entre \(A\) et \(B\), démontrer que : \[ P_0+\rho g h=P_0+\frac{1}{2}\rho v_B^2 \] où \(P_0\) est la pression atmosphérique dont on rappellera la valeur.
3. En déduire alors la formule de Torricelli.
Voir l'indice
1. Utilisez la conservation du débit volumique (Prop. 2 du cours) : \(S_A v_A = S_B v_B\). Le récipient est très large (\(S_A\)) par rapport au trou (\(S_B\)), donc \(S_A \gg S_B\).
2. Appliquez la loi de Bernoulli (Th. 2) entre A et B. \(P_A\) et \(P_B\) sont tous deux ouverts à l'air libre, ils sont donc égaux à la pression atmosphérique \(P_0\). On pose \(z_B=0\) et \(z_A=h\). Utilisez le résultat de la Q1 pour simplifier \(v_A\).
3. Isolez \(v_B\) à partir de l'équation de la Q2.
Afficher le corrigé
Corrigé non disponible pour le moment.
Exercice 2 (Tube convergent) 🌶️ 🌶️ 🌶️
On considère la situation suivante, une particule fluide traverse un tube convergent (dont la section diminue) :
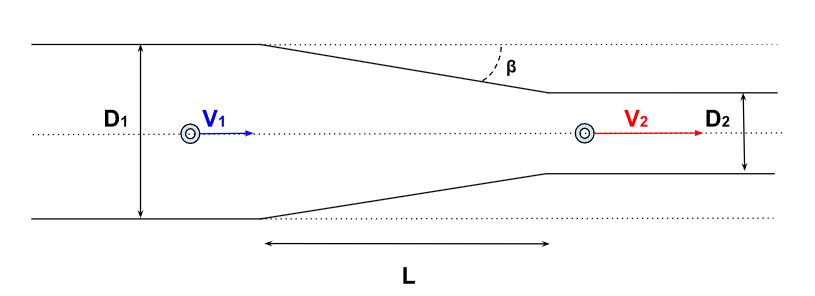
On note \(D_1\) le diamètre de la partie amont du tube (avant déformation) et \(V_1\) la vitesse de la particule fluide dans cette première partie, on note \(D_2\) le diamètre de la partie aval du tube (après déformation) et \(V_2\) la vitesse de la particule fluide dans cette seconde partie. \(L\) représente la longueur sur laquelle le tube rétrécit et son angle de rétrécissement est donnée par \(\beta\).
Le fluide considéré est parfait subissant un écoulement permanent.
1. Rappeler la définition de fluide parfait.
2. Comparer les vitesses \(V_1\) et \(V_2\) dans le cas d'un tube convergent.
3. En supposant qu'en amont et en aval le tube est cylindrique, déterminer l'expression du rapport \(\frac{D_1}{D_2}\) en fonction de \(V_1\) et \(V_2\).
4. Exprimer la différence \(D_1-D_2\) en fonction de \(L\) et \(\beta\).
5. Si l'on cherche à avoir en sortie une vitesse \(V_2\) dix fois plus élevée que \(V_1\), déterminer la valeur de la longueur \(L\) qu'il faut sachant que \(D_1=10\) cm et \(\beta=10^\circ\).
Voir l'indice
2. Utilisez la conservation du débit volumique (Prop. 2) : \(S_1 V_1 = S_2 V_2\). Comme le tube converge, \(S_2 < S_1\).
3. La section \(S\) d'un tube cylindrique de diamètre \(D\) est \(S = \pi (D/2)^2 = \frac{\pi D^2}{4}\). Remplacez cela dans la conservation du débit.
4. Regardez le schéma. Vous pouvez dessiner un triangle rectangle dont l'hypoténuse est \(L\) et le côté opposé est \((D_1-D_2)/2\).
5. Utilisez la Q3 pour trouver \(D_2\) (sachant que \(V_2 = 10V_1\)). Puis utilisez la Q4 pour trouver \(L\).
Afficher le corrigé
Corrigé non disponible pour le moment.
Exercice 3 (Application du théorème de Bernoulli) 🌶️ 🌶️ 🌶️
On considère deux points \(A\) et \(B\) confinés dans un tube de courant. On note \(z_A\) l'altitude du point \(A\), \(z_B\) l'altitude du point \(B\) de telle sorte que \(z_A<z_B\). On suppose qu'un fluide parfait s'écoule en \(A\) à un débit volumique \(D_v\). La pression en \(A\) est notée \(P_A\) et on cherche à déterminer la pression en \(B\).
En \(A\), le tube de courant a un diamètre \(D_A\) et en \(B\), un diamètre \(D_B\).
1. Représenter la situation par un schéma.
2. Déterminer l'expression de la pression en \(B\).
3. Application numérique : \(z_A=5\) m, \(z_B=10\) m, \(D_v=500\) L.s⁻¹, \(P_A=1\) bar, \(D_A=50\) cm et \(D_B=75\) cm.
Voir l'indice
2. Appliquez la loi de Bernoulli (Th. 2) entre A et B : \(P_A+\rho g z_A+\frac{1}{2}\rho v_A^2=P_B+\rho g z_B+\frac{1}{2}\rho v_B^2\). Isolez \(P_B\).
3. Vous devez d'abord calculer \(v_A\) et \(v_B\). Utilisez la conservation du débit : \(D_v = S_A v_A = S_B v_B\). N'oubliez pas de convertir **toutes** les unités en S.I. (L/s en m³/s, bars en Pa, cm en m).
Afficher le corrigé
Corrigé non disponible pour le moment.
En route vers le supérieur
Exercice 4 (Le siphon) ❤️ 🌶️ 🌶️ 🌶️
On représente la situation suivante où l'on vide un réservoir grâce à un différentiel de pression créé par un tube d'air :
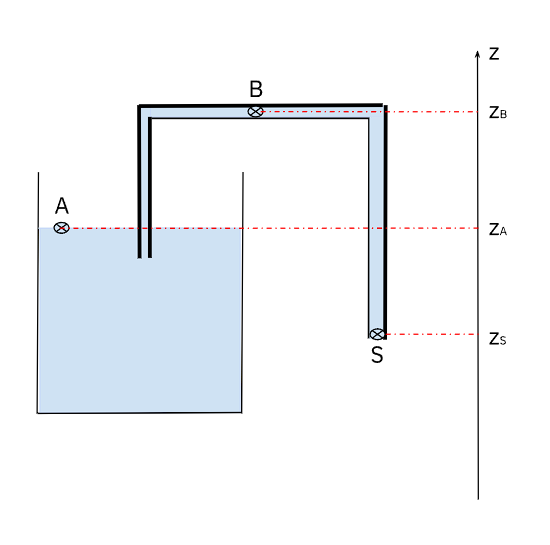
Ici, l'on considère trois points \(A\), \(B\) et \(S\) : un à la surface du liquide contenue dans le réservoir, un point situé dans la partie supérieure du tube de vidange, un autre situé en sortie du siphon.
On repère à l'aide d'un axe \(z\), les altitudes de \(A\), \(B\) et \(S\) par \(z_A\), \(z_B\) et \(z_S\) respectivement.
Le siphon est un tube cylindrique de diamètre \(D=10\) mm. Le réservoir contient un fluide supposé parfait, le débit entrant dans le siphon est faible dans l'écoulement peut être supposé lent, l'accélération de la pesanteur peut être supposée constante et est notée \(\vec{g}\) valant 9,81 m.s⁻². On note \(h\) la différence d'altitude entre \(B\) et \(A\) et \(H\), la différence d'altitude entre \(A\) et \(S\) valant 2,5 m. On note \(p\) la norme du poids du fluide à l'état initial par unité de volume : \[ p=\frac{mg}{V} \] où \(m\) est la masse du fluide et \(V\) son volume initial. On prend \(p=10\) kN.m⁻³.
1. Calculer la vitesse d'écoulement en \(S\), notée \(V_S\), à l'aide du théorème de Bernoulli appliqué entre \(A\) et \(S\).
2. En déduire le débit volumique tout au long du siphon.
3. Déterminer l'expression qui donne la pression en \(B\), notée \(P_B\), en fonction de la pression atmosphérique \(P_0\), \(h\), \(H\) et \(p\).
4. Application numérique de \(P_B\) : on suppose que \(h=0,5\) m.
5. Pour quelle valeur de \(h\) peut-on étudier le modèle du siphon ?
Voir l'indice
1. Appliquez Bernoulli entre A et S. \(P_A = P_S = P_{atm}\) (pression atmosphérique). On suppose \(v_A \approx 0\) (grand réservoir). La différence d'altitude est \(z_A - z_S = H\).
2. Utilisez \(D_v = S_S \times V_S\), où \(S_S\) est la section du tube de diamètre \(D\).
3. Appliquez Bernoulli entre A et B. \(P_A = P_{atm}\), \(v_A \approx 0\). La vitesse \(v_B\) est la même que \(v_S\) (fluide incompressible, tube de section constante). La différence d'altitude est \(z_B - z_A = h\). Notez que \(p = \rho g\).
5. Le siphon ne fonctionne que si le fluide reste liquide. La pression en tout point doit être supérieure à la pression de vapeur saturante (qu'on approxime ici à 0). Calculez le \(h\) maximal pour lequel \(P_B > 0\).
Afficher le corrigé
Corrigé non disponible pour le moment.
Exercice 5 (Tube de pitot) ❤️ 🌶️ 🌶️ 🌶️
On considère un dispositif de mesure de vitesse en utilisant le théorème de Bernoulli. Il est utilisé comme un capteur de vitesse pour les engins de l'aviation civile - en particulier, les avions de ligne. Le dispositif est le suivant :
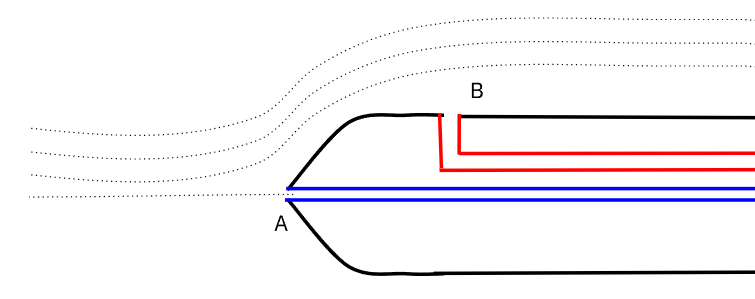
En pointillé, ce sont les lignes de courant de l'air arrivant à l'entrée du tube, en \(A\), on représente une première entrée sur laquelle les lignes de courant viennent se casser (c'est ce qu'on appelle un point d'arrêt) et en \(B\), une entrée à la surface du tube mais qui se situe sur une ligne de courant.
1. Justifier qu'en \(A\), la vitesse d'entrée est nulle.
2. Justifier qu'en \(B\), la vitesse d'entrée est égale à celle de l'avion.
3. Exprimer la différence de pression entre \(A\) et \(B\) notée \(\Delta_{A\rightarrow B}P\) en fonction de la vitesse de l'avion notée \(v\).
4. Calculer \(\Delta_{A\rightarrow B}P\) si \(v=1000\) km.h⁻¹.

Photographie d'une sonde pitot, SOURCE : France Bleu
Voir l'indice
1. Le point A est un "point d'arrêt" (stagnation point). Le fluide arrive de face et est stoppé net à cet endroit pour mesurer la pression totale.
2. Le point B est un trou sur la paroi, parallèle à l'écoulement. Il mesure la pression statique du fluide sans perturber sa vitesse, qui est la vitesse de l'air par rapport à l'avion (donc \(v\)).
3. Appliquez la loi de Bernoulli entre A et B. On suppose que les points sont à la même altitude (\(z_A = z_B\)). Vous avez \(v_A = 0\) et \(v_B = v\). Isolez \(\Delta P = P_A - P_B\).
4. N'oubliez pas de convertir la vitesse en m/s ! (1000 km/h \(\approx\) 278 m/s). Il vous faudra la masse volumique de l'air \(\rho_{air} \approx 1.225\) kg/m³ (non donnée mais standard).
Afficher le corrigé
Corrigé non disponible pour le moment.