Terminale : Mécanique des fluides
Jusqu'à là, nous avons appris à étudier le mouvement des systèmes assimilables à des points matériels (hypothèse du point matériel, cf cours sur la dynamique du point matériel) et le mouvement des gaz supposés parfaits avec le modèle du gaz parfait (cf. cours sur la thermodynamique). En revanche, à ce stade, il nous est impossible de modéliser le mouvement de n'importe quel gaz et liquide... C'est l'objet de ce chapitre, les étudier sous certaines conditions : lorsqu'ils sont assimilables à un fluide.
📚 Table des matières
1. Introduction à la notion de fluide
Définition 1. (Milieu matériel)
On dit d'un milieu qu'il est matériel lorsqu'il est composé d'atomes.
Remarque : La vide est le seul milieu qui n'est pas matériel.
Définition 2. (Contrainte)
On appelle contrainte, toute force surfacique (force par unité de surface). Si l'on note \(\sigma\) la contrainte d'une force \(\vec{F}\) sur une surface \(S\) alors :
Remarque (HP) : On peut décrire chaque contrainte avec deux composantes distinctes. Une composante dite normale et une composante dite tangentielle. Si l'on considère un point \(M\) d'une surface, il est possible de définir en ce point un plan tangent (localement alignée à la surface) et une droite normale à ce plan tangent (perpendiculaire au plan) passant par \(M\). Si l'on considère le vecteur contrainte écrit en \(M\), notée \(\vec{\sigma}(M)\), ce vecteur aura une composante dans le plan tangent en \(M\) et suivant la droite normale en \(M\). On note respectivement ces composantes \(\vec{\sigma}_t(M)\) et \(\vec{\sigma}_n(M)\). On en déduit alors : \[ \boxed{\vec{\sigma}(M)=\vec{\sigma}_t(M)+\vec{\sigma}_n(M)} \] En notant \(\sigma(M)\) la norme du vecteur \(\vec{\sigma}(M)\), on en déduit que : \[ \boxed{\sigma(M)=\sqrt{||\vec{\sigma}_t(M)||^2+||\vec{\sigma}_n(M)||^2}} \] \(\sigma_t(M)\) représente la contrainte tangentielle en \(M\) et \(\sigma_n(M)\) représente la contrainte normale en \(M\).
Définition 3. (Milieu matériel déformable)
Un milieu matériel est déformable s'il change de forme lorsqu'il est soumis à des contraintes.
Remarque : On dit d'un milieu qu'il est parfaitement déformable lorsqu'il change de forme même s'il est soumis à de faibles contraintes.
Définition 4. (Fluide)
Un fluide est un milieu matériel qui est parfaitement déformable.
Remarque : La définition donnée de fluide est partiellement rigoureuse. Il faudrait plutôt parler de milieu matériel parfaitement déformable aux contraintes tangentielles. Les molécules d'un fluide sont au mouvement les unes par rapport aux autres.
Remarque : Les fluides regroupent les liquides et les gaz. Un plasma est un état de la matière dans lequel les particules sont ionisées à une température élevée. Un plasma est aussi un fluide.
En mécanique des fluides, on distingue deux sous-domaines : la statique des fluides où l'on étudie les fluides au repos et la dynamique des fluides où l'on étudie les fluides en mouvement.
2. Propriétés d'un fluide
Définition 5. (La masse volumique du fluide)
En notant \(m\) la masse du fluide et \(V\) son volume, la masse volumique notée \(\rho\) se définit comme :
Définition 6. (La densité du fluide)
En notant \(m\) la masse du fluide, \(V\) son volume et \(\rho_{ref}\) la masse volumique de référence du fluide, la densité notée \(d\) se définit comme :
Définition 7. (La viscosité du fluide)
La viscosité d'un fluide, notée \(\eta\), est une grandeur qui caractérise à quel point le fluide possède des frottements internes. De manière équivalente, cela désigne sa capacité à s'écouler.
Remarque : Un fluide de grande viscosité résiste davantage aux effets de gravité lorsqu'il s'écoule. Inversement, un fluide de faible viscosité s'écoule plus facilement.
Remarque : Le miel a une plus grande viscosité que l'eau liquide.
Définition 8. (Fluide parfait)
Un fluide est dit parfait lorsque sa viscosité est nulle. On parle aussi de fluide idéal.
Remarque : Tout fluide de viscosité non nulle est appelée fluide réel.
Définition 9. (Fluide statique)
Un fluide est dit statique lorsqu'il est au repos. Le fluide n'est pas en mouvement.
Définition 10. (Fluide incompressible)
Un fluide est dit incompressible lorsque le volume qu'il occupe au repos ne peut être réduit même s'il est soumis à des contraintes. En d'autres termes, sa masse volumique doit être uniforme (la même en tout point du fluide) et constante (indépendante du temps).
3. Statique des fluides
3.1. Corps immergée : poussée d'Archimède
Lorsqu'un corps est immergée dans un fluide au repos (fluide statique), ce dernier subit une force qui s'oppose à son mouvement naturel, sa chute. On appelle cette force la poussée d'Archimède. Elle s'oppose alors à la force gravitationnelle subie par le corps, son propre poids.
On veut que cette force soit nulle lorsque le corps n'est pas plongé dans le fluide au repos, elle doit être plus grande que le poids lorsque sa densité est plus petite que celle du fluide et enfin, le corps doit être capable de flotter lorsque cette force sera plus grande que son poids.
On fera l'hypothèse que les grandeurs liées au fluide, dans la suite, seront constantes.
Définition 11. (Poussée d'Archimède)
La poussée d'Archimède est la force qui s'oppose au poids d'un corps lorsqu'il est immergé dans un fluide de masse volumique \(\rho\). En notant \(\vec{g}\) l'accélération de la pesanteur dirigée vers le bas et \(V_i\) le volume de la partie immergée du corps étudié, la poussée d'Archimède notée \(\vec{\Pi}\) s'écrit :
Remarque : Attention, à ne pas faire de confusion dans cette formule. C'est bien la masse volumique \(\rho\) du fluide dans lequel se trouve le corps étudié et \(V_i\) le volume de la partie immergée du corps.
Observons que cette expression de force s'oppose bien au poids colinéaire à \(\vec{g}\). Connaissant \(\rho\) et \(V_i\), on peut savoir si un corps sera capable ou non de flotter à la surface du fluide considéré.
3.2. Loi de la statique des fluides
Théorème 1. (Loi de la statique des fluides)
Soit un fluide incompressible et au repos de masse volumique \(\rho\). On considère deux points \(A\) et \(B\) situés sur le même axe vertical dirigé vers le haut d'altitude respectives \(z_A\) et \(z_B\) et de pression respectives \(P_A\) et \(P_B\). L'identité suivante est toujours vérifiée, on l'appelle loi de la statique des fluides (incompressibles) :
Remarque : Pour aller plus loin, si l'on utilise les notations avec les différentielles \(dP\) et \(dz\) alors, on peut récrire la loi de la statique des fluides comme : \[ dP=-\rho g dz \] ce qui s'écrit de manière équivalente, \[ \frac{dP}{dz}=-\rho g \] lorsque l'axe est dirigé vers le haut. C'est cette relation qui établit le théorème 1. Elle se démontre en réalisant un bilan des forces de pression sur un volume élémentaire de fluide, appelée particule fluide, définie à l'échelle mésoscopique (entre \(10^{-8}\) et \(10^{-4}\) mètres). Sa démonstration est hors-programme.
4. Écoulement d'un fluide
Définition 12. (Ligne de courant)
Une ligne de courant est une des trajectoires suivies par les molécules au sein d'un fluide lors son écoulement.
Définition 13. (Caractéristiques de l'écoulement d'un fluide)
L'écoulement d'un fluide est défini à partir de certaines données. On parle alors des caractéristiques de l'écoulement. Pour définir l'écoulement, il nous faut alors connaître la vitesse en chaque point du fluide, la pression en chaque point du fluide et la masse volumique en chaque point du fluide.
Remarque : Un fluide étant composé d'une infinité de points définis dans un volume \(V\), on appelle l'ensemble des vitesses de ses points, le champ de vitesse noté \(\vec{v}(M,t)\). On fait la même chose avec la pression et la masse volumique pour définir un champ de pression \(P(M,t)\) et la masse volumique (non uniforme à priori) \(\rho(M,t)\).
Définition 14. (Écoulement permanent)
L'écoulement d'un fluide est permanent lorsque ses caractéristiques sont indépendantes du temps. En d'autres termes, le champ de vitesse, le champ de pression et la masse volumique sont indépendants du temps.
Définition 15. (Le débit volumique)
Le débit volumique notée \(D_v(t)\) représente la variation de volume du fluide à travers une surface \(S\) par laquelle il s'écoule au cours du temps. Si l'on note \(dV\) cette variation alors,
Proposition 1. (Le débit volumique d'un fluide incompressible)
Le débit volumique d'un fluide incompressible s'exprime comme le produit de la surface traversée par ce fluide et sa vitesse de traversée. En notant \(S\) cette surface et \(v\) la vitesse de traversée, le débit volumique \(D_v(t)\) s'exprime comme :
Remarque : Remarquons le résultat sous-jacent suivant : \[ \boxed{\forall M\in S, \space v(M,t)=v(t)} \] sous les mêmes hypothèses.
Proposition 2. (Conservation du débit volumique)
Le débit volumique d'un fluide incompressible en écoulement permanent se conserve au cours du temps. En tout point \(M\) du fluide incompressible en écoulement permanent, on a :
Remarque : On considère un tuyau infini suivant l'axe \(\vec{z}\) de section variable. On note \(S\) la fonction qui définit la surface du tuyau en \(z\), on note \(S(z)\) cette surface. On définit la fonction \(v\) qui définit la vitesse le long de l'axe de \(z\) et l'on note \(v(z)\) la vitesse en \(z\) au sein d'un fluide incompressible traversant le tuyau. On suppose l'écoulement du fluide permanent. On en déduit que le produit suivant se conserve : \[ \forall z\in\mathbb{R}, \space S(z)v(z)=cste \]
Théorème 2. (Loi de Bernoulli)
Si l'on considère un fluide parfait et incompressible subissant un écoulement permanent alors son énergie volumique se conserve le long d'une ligne de champ. Si l'on considère deux points \(A\) et \(B\) et les deux triplets \((P_A,z_A,v_A)\) et \((P_B,z_B,v_B)\) représentant respectivement la pression, l'altitude et la vitesse en chaque point alors, on a toujours :
Remarque : Une hypothèse cachée pour justifier de la conservation de l'énergie volumique est de supposer que le champ de pesanteur (gravitationnel) de la Terre est constant. Dans ce cas, le théorème 2 s'applique toujours.
5. Dynamique des fluides incompressibles
Définition 16. (Pression statique)
Si l'on note \(P\) la pression d'un fluide au repos constante et uniforme, alors la pression statique notée \(P_s\) est égale à la pression \(P\) :
Remarque : Par définition de fluide statique (au repos), on comprend cette définition.
Définition 17. (Pression hydrostatique)
Si l'on considère un fluide de masse volumique \(\rho\) à l'altitude \(z\) dans un champ de pesanteur d'intensité uniforme notée \(g\) alors, la pression hydrostatique notée \(P_h\) est définie comme :
Remarque : Cette définition provient de la loi de la statique des fluides incompressibles et au repos.
Définition 18. (Pression dynamique)
Si l'on considère un fluide de masse volumique \(\rho\) se déplaçant à la vitesse \(v\), la pression dynamique notée \(P_d\) est définie comme :
Remarque : A l'aide des trois pressions précédemment définies, on peut écrire différemment la loi de Bernoulli* :
Proposition 3. (Effet Venturi)
Soit un fluide parfait et incompressible subissant un écoulement permanent. Si la section par laquelle le fluide s'écoule diminue alors la vitesse du fluide augmente et sa pression diminue.
Preuve
Si la section traversée diminue, comme le débit se conserve d'après la proposition 2, la vitesse du fluide à travers cette surface augmente. Si la vitesse augmente, son carré aussi et donc d'après la loi de Bernoulli, comme on suppose l'écoulement à altitude constante alors la variation de pression diminue. Ce qui implique que la pression diminue.
Pour terminer, nous allons considérer un récipient de hauteur \(h\) dont on creuse un trou vertical de section \(S\) dans son fond. Nous allons établir la formule de Torricelli qui énonce que la vitesse en \(B\) s'écrit : \[ v_B=\sqrt{2gh} \] avec \(g\) l'intensité de pesanteur supposée constante.
On représente la situation étudié comme suit :
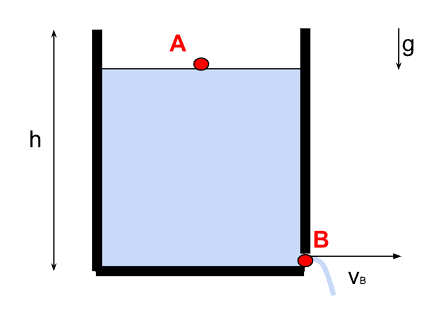
Le fluide supposé parfait, incompressible est représenté en bleu. On suppose que son écoulement à travers \(B\) est permanent et on note \(S_B\) la section du trou en \(B\). On suppose initialement, l'altitude de \(A\) valant \(h\) et qu'au cours du temps, cette dernière diminue. On note \(g\) l'intensité de la pesanteur dont le vecteur est dirigé vers le bas. On note \(v_A\) la vitesse du point \(A\), \(v_B\) celle du point \(B\) et \(S_A\) la section en \(A\). Au vu de la représentation, on peut suppose \(S_A \gg S_B\).
Comme le débit volumique se conserve, celui en \(A\) et en \(B\) sont égaux d'où : \[ S_Av_A=S_Bv_B \] Comme on a supposé \(S_A \gg S_B\) alors il en suit que \(v_A \ll V_B\) donc il est crédible de négliger la valeur de la vitesse en \(A\) car quasi-nulle.
Il existe une ligne de courant allant de \(A\) à \(B\) qui permet d'écrire avec la loi de Bernoulli, que sur cette ligne de courant, l'énergie volumique est conservée d'où : \[ P_A+\rho g z_A+\frac{1}{2}\rho v_A^2=P_B+\rho g z_B+\frac{1}{2}\rho v_B^2 \] L'égalité se simplifie comme suit avec \(z_A=h\) initialement et \(z_B=0\) : \[ P_A+\rho g h=P_B+\frac{1}{2}\rho v_B^2 \] Or \(A\) et \(B\) sont en contact avec l'extérieur donc ces points ont même pression qu'on notera \(P\) d'où : \[ P+\rho g h=P+\frac{1}{2}\rho v_B^2 \] On en déduit finalement que : \[ v_B=\sqrt{2gh} \] C'est un exercice très classique dont le raisonnement doit être compris et maîtrisé.