Terminale : Exercices sur l'approche énergétique des mouvements
La mention ❤️ indique que la méthode de résolution proposée par l'exercice est à maîtriser et à savoir refaire, on peut aussi parler d'exercice classique. Finalement, chaque exercice possède sa propre difficulté : 🌶️ pour un exercice facile, 🌶️🌶️ pour un exercice de difficulté moyenne et 🌶️🌶️🌶️ pour un exercice difficile dans sa résolution.
Exercices d'application
Exercice 1 (Étude du pendule simple) ❤️ 🌶️ 🌶️ 🌶️
On considère une tige de longueur \(l\) qui oscille autour du point \(O\) dans le plan \((O,x,y)\). On attache au bout de la tige une masse \(m\) dont la position varie au cours du temps, on note \(M(t)\), la position de la masse \(m\) à l'instant \(t\). On prendre \(t_0\) comme le temps initial auquel on lâche la tige et la masse. On supposera que la tige est de masse nulle. On suppose que la masse \(m\) ne subit que l'effet de son propre poids et la tension du fil.
Le but de cet exercice est d'établir l'équation différentielle sur la position de la masse \(m\). On admet que le mouvement de la masse \(M\) ne dépend que de la valeur d'angle \(\theta\).
.png)
1. Justifier que l'angle \(\theta\) est une fonction du temps.
2. Montrer que l'énergie mécanique se conserve au cours du temps.
En se plaçant dans le repère de Frenet, on établit que la vitesse du point \(M\) a pour expression : \[ v_M(t)=l\frac{d\theta(t)}{dt}\cdot\vec{t} \]
3. Refaire la figure en plaçant le repère de Frenet en \(M\) en prenant comme origine le point \(O\).
4. Montrer que l'énergie cinétique de la masse \(m\) s'écrit : \[ E_c(t)=\frac{1}{2}ml^2\left(\frac{d\theta(t)}{dt}\right)^2 \]
5. En considérant deux positions successives de la masse \(m\), entre les instants \(t\) et \(t+dt\), montrer que la différence d'altitude selon l'axe \(y\), notée \(dy\) est donnée par : \[ dy=l(1-\cos(d\theta)) \] où \(d\theta\) est l'écart angulaire entre les deux positions.
6. Montrer que l'énergie potentielle de la masse \(m\) s'écrit : \[ E_p(t)=mgl(1-\cos(\theta(t))) \]
7. A partir de la conservation de l'énergie mécanique, expliquer pourquoi on a : \[ \frac{dE_m(t)}{dt}=0 \]
8. En déduire l'équation différentielle suivante : \[ \frac{d^2\theta(t)}{dt^2}+\omega_0^2\sin(\theta(t))=0 \] où \(\omega_0\) est à exprimer en fonction des constantes \(l\) et \(g\).
Voir l'indice
2. Faites le bilan des forces. La tension \(\vec{T}\) est perpendiculaire au déplacement, son travail est nul. Le poids \(\vec{P}\) est une force conservative. L'énergie mécanique se conserve donc.
4. Utilisez \(E_c = \frac{1}{2}mv_M^2\) et l'expression de \(v_M(t)\) donnée.
6. Exprimez l'altitude \(y_M\) en fonction de \(l\) et \(\theta\) (avec \(y=0\) au point le plus bas). L'énergie potentielle de pesanteur est \(E_p = mg y_M\).
7. & 8. \(E_m = E_c + E_p = \text{constante}\). Dérivez cette expression par rapport au temps. N'oubliez pas que \(\frac{d(\cos\theta)}{dt} = -\sin(\theta) \cdot \frac{d\theta}{dt}\) et \(\frac{d}{dt}\left( (\frac{d\theta}{dt})^2 \right) = 2 \cdot \frac{d\theta}{dt} \cdot \frac{d^2\theta}{dt^2}\).
Afficher le corrigé
Corrigé non disponible pour le moment.
Exercice 2 (Énergie mécanique d'un corps céleste sur une orbite circulaire) ❤️ 🌶️ 🌶️ 🌶️
Le but de cet exercice est d'établir un résultat fondamental : si un corps céleste de masse \(m\) a une trajectoire circulaire alors son énergie mécanique, notée \(E_m\), se conserve et vaut : \[ E_m=-G\frac{mM_{\circ}}{2r} \] où \(M_{\circ}\) est la masse de son corps attracteur.
1. Si l'on considère uniquement l'influence du corps attracteur sur le corps céleste étudié, montrer que l'énergie mécanique du corps céleste se conserve.
2. Représenter le système étudié, qu'on assimilera à un point matériel de masse \(m\) et noté \(C\), gravitant autour de son corps attracteur qu'on assimilera aussi à un point matériel de masse \(M_\circ\) et noté \(A\).
3. En revenant à la définition du travail d'une force, montrer que l'énergie potentielle de gravitation de \(C\) existe, qu'on notera \(E_{pg}\), et est égale à : \[ E_{pg}=-G\frac{mM_\circ}{r} \]
4. Dans le cas d'un mouvement circulaire, exprimer la valeur de la vitesse du corps céleste \(C\).
5. Montrer alors que l'énergie cinétique de \(C\) notée \(E_c\) s'écrit : \[ E_c=G\frac{mM_\circ}{2r} \] (Note : il y a une erreur de signe dans le LaTeX, l'énergie cinétique est positive)
6. En déduire que l'énergie mécanique de \(C\) s'écrit : \[ E_m=-G\frac{mM_{\circ}}{2r} \]
Voir l'indice
1. La force gravitationnelle est une force conservative. En l'absence de forces non conservatives (frottements, etc.), l'énergie mécanique se conserve.
4. Appliquez le PFD au corps \(C\). La force \(\vec{F}_g\) est égale à \(m\vec{a}\). En mouvement circulaire uniforme, l'accélération est centripète et vaut \(a = v^2/r\).
5. Utilisez l'expression de \(v\) (ou \(v^2\)) de la Q4 et injectez-la dans \(E_c = \frac{1}{2}mv^2\).
6. Faites la somme : \(E_m = E_c + E_{pg}\).
Afficher le corrigé
Corrigé non disponible pour le moment.
Exercice 3 (Énergie potentielle électrique) 🌶️ 🌶️ 🌶️
Le but de cet exercice est de montrer que l'énergie potentielle d'une charge \(q\), notée \(E_p\), résultante de la présence d'une charge \(Q\) a pour expression : \[ E_p=K\frac{qQ}{r} \] où \(r\) désigne la distance entre les deux charges.
A partir de la définition du travail d'une force, montrer le résultat souhaité.
Voir l'indice
La variation d'énergie potentielle est l'opposé du travail de la force conservative : \(\Delta E_p = -W(\vec{F}_e)\).
Calculez le travail \(W = \int_{A}^{B} \vec{F}_e \cdot d\vec{l}\), où \(\vec{F}_e = K\frac{qQ}{r^2}\vec{u}_r\). L'intégrale de \(\frac{1}{r^2} dr\) est \(-\frac{1}{r}\).
Par convention, on fixe \(E_p = 0\) lorsque \(r \to \infty\).
Afficher le corrigé
Corrigé non disponible pour le moment.
En route vers le supérieur
Exercice 4 (Étude d'un ressort élastique) ❤️ 🌶️ 🌶️ 🌶️
Première partie : étude dynamique du mouvement
Selon un axe horizontale \(x\), on fixe une masse \(m\) à un ressort de raideur \(k\) et de longueur à vide (au repos) \(l_0\).
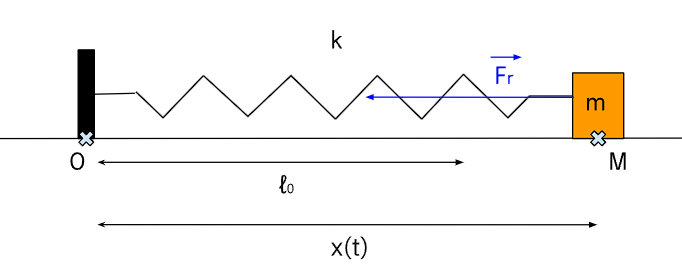
On appelle \(\vec{F_r}\) la force subie par la masse \(m\) lorsqu'on tire sur le ressort (pour rappel, elle est attachée au ressort), la force de rappel élastique et elle vaut : \[ \vec{F_r}=-k(x(t)-l_0)\vec{x} \]
1. En ne considérant que l'action de la pesanteur et élastique, établir que : \[ a_x(t)+k(x(t)-l_0)=0 \] (Note : erreur dans le LaTeX, il manque \(m\). L'équation devrait être \(a_x(t) + \frac{k}{m}(x(t)-l_0) = 0\))
2. En posant \(X(t)=x(t)-l_0\), établir l'équation différentielle suivante : \[ \frac{d^2X(t)}{dt^2}+\omega_0^2 X(t)=0 \]
3. Montrer que les fonctions de la forme suivante sont solution de l'équation différentielle précédente : \[ X:t\mapsto A\sin(\omega_0 t)+B\cos(\omega_0 t) \]
Du postulat d'élasticité du ressort, on en déduit la relation suivante appelée loi de Hooke : \[ \sigma=E\cdot\varepsilon \] où \(\sigma\) désigne la contrainte suivant l'axe \(x\), \(E\) une constante désignant la rigidité du ressort et \(\varepsilon\) le rapport entre le déplacement relatif \(X\) et la longueur à vide \(l_0\).
4. Montrer que la constante de raideur \(k\) s'exprime en fonction de la constante de rigidité \(E\) : \[ k=\frac{ES}{l_0} \] où \(S\) est la section du ressort.
Deuxième partie : étude énergétique du mouvement
5. Montrer que l'énergie cinétique de la masse \(m\) vaut : \[ E_c(t)=\frac{1}{2}m\left(\frac{dX(t)}{dt}\right)^2 \]
6. En revenant à la définition du travail d'une force, établir que l'énergie potentielle élastique s'écrit : \[ E_p(t)=\frac{1}{2}kX^2(t) \]
7. En admettant que l'énergie mécanique se conserve, retrouver l'équation différentielle précédente : \[ \frac{d^2X(t)}{dt^2}+\omega_0^2 X(t)=0 \]
Voir l'indice
1. PFD : \(m\vec{a} = \sum \vec{F}\). Les forces sont Poids, Réaction Normale, Force de rappel \(\vec{F}_r\). Le poids et la réaction se compensent sur un plan horizontal. \(\vec{a} = a_x \vec{x}\).
5. \(v = \frac{dx}{dt}\). Or \(X(t) = x(t) - l_0\), donc \(\frac{dX}{dt} = \frac{dx}{dt}\). \(E_c = \frac{1}{2}mv^2\).
6. \(\Delta E_p = -W(\vec{F}_r) = - \int \vec{F}_r \cdot d\vec{l}\). Avec \(\vec{F}_r = -kX \vec{x}\) et \(d\vec{l} = dX \vec{x}\).
7. \(E_m = E_c + E_p = \text{Cste}\). Dérivez cette somme par rapport au temps et posez \(\frac{dE_m}{dt} = 0\).
Afficher le corrigé
Corrigé non disponible pour le moment.
Exercice 5 (Illustration des énergies) 🌶️ 🌶️ 🌶️
Représenter sur un graphique sans tenir compte de l'échelle l'allure des énergies cinétique, potentielle et mécanique dans les situations suivantes.
1. Cas de la chute libre sans vitesse initiale.
2. Cas de la chute libre avec vitesse initiale.
3. Cas d'un projectile lancé à une certaine inclinaison avec une vitesse initiale.
4. Cas du glissement d'une brique sur le sol sans inclinaison jusqu'à son arrêt complet.
Voir l'indice
Tracez trois courbes : \(E_c\), \(E_p\), et \(E_m\).
1, 2, 3 : Pas de frottements \(\implies\) \(E_m = \text{Cste}\) (ligne horizontale). \(E_p = mgz\), \(E_c = E_m - E_p\).
4 : Frottements \(\implies\) La force non-conservative travaille. \(E_m\) diminue au cours du temps (probablement de façon linéaire ou quadratique selon le modèle de frottement) jusqu'à 0.
Afficher le corrigé
Corrigé non disponible pour le moment.
Exercice 6 (Roulement d'un cylindre sur une pente inclinée) 🌶️ 🌶️ 🌶️
On considère un cylindre qui roule sur une pente inclinée d'un angle \(\alpha\) purement lisse par rapport à l'horizontale. On note \(m\) la masse du cylindre et on assimile à un point matériel \(M\) de masse \(m\) l'ensemble du cylindre. On lâche sans vitesse initiale le cylindre en \(A\) et on cherche à déterminer sa vitesse en \(B\) puis le temps mis pour faire le trajet \(AB\).
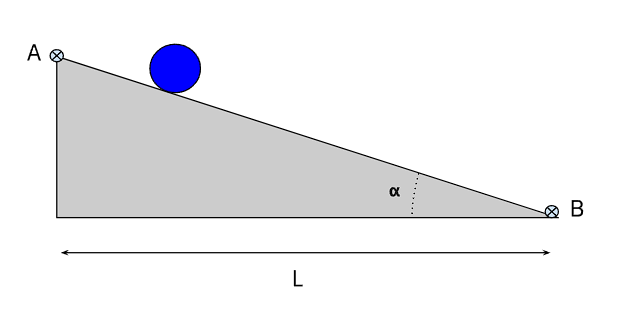
1. Quelle hypothèse de l'énoncé permet de négliger les frottements ?
2. Quelle information ne doit-on ne pas considérer si l'on assimile notre cylindre à un point matériel ?
3. A partir du théorème de l'énergie cinétique, déterminer l'expression de la vitesse du cylindre en \(B\).
4. En utilisant le principe fondamental de la dynamique, déterminer le temps mis par le cylindre pour parcourir la distance \(AB\).
Voir l'indice
1. "purement lisse".
2. Le fait qu'il "roule" (rotation). Un point matériel ne peut pas tourner sur lui-même.
3. Appliquez \(\Delta E_c = W_{ext}(\vec{F})\). La seule force qui travaille est le poids. \(E_c(B) - 0 = W(\vec{P})\). Le travail du poids est \(mg \Delta z = mg (z_A - z_B)\).
4. PFD : \(m\vec{a} = \sum \vec{F} = \vec{P} + \vec{R}\). Projetez sur l'axe de la pente pour trouver \(a\). Puis utilisez \(x(t) = \frac{1}{2} a t^2\) pour trouver \(t\) quand \(x = AB\).
Afficher le corrigé
Corrigé non disponible pour le moment.