Terminale : Aspect énergétique du mouvement
📚 Table des matières
1. Travail d'une force
Définition 1. (Travail d'une force)
Le travail d'une force \(\vec{F}\), noté \(W\left(\vec{F}\right)\), pour une force constante sur un déplacement \(\overrightarrow{AB}\), est définie par la formule suivante :

Figure 1. Représentation graphique des vecteurs
Cette notion bien que fondamentale, est cependant difficile à interpréter. En fait, le travail d'une force représente l'énergie fournie par la force au système lorsque ce dernier est en déplacement.
Le travail \(W\left(\vec{F}\right)\) s'exprime donc en Joules (J).
Quelques interprétations.
On introduit alors le vocabulaire suivant pour caractériser un travail :
- Si \(W\left(\vec{F}\right) \geq 0\) (i.e. \(\alpha \in [0,\frac{\pi}{2}]\)), on dira que le travail est moteur (il ne s'oppose pas au mouvement).
- Si \(W\left(\vec{F}\right) \leq 0\) (i.e. \(\alpha \in [\frac{\pi}{2},\pi]\)), on dira que le travail est résistant (il s'oppose au mouvement).
Exemple (Travail du poids). On se place dans la situation suivante :
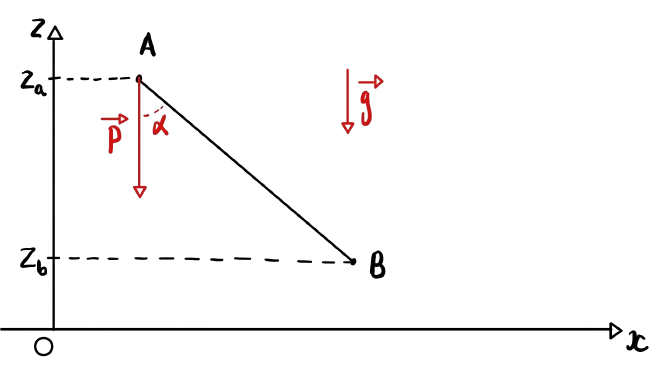
Figure 2. Représentation graphique de la situation
On souhaite calculer le travail du poids. Pour cela, on applique simplement la formule :
\[ W(\vec{P}) = m \vec{g} \cdot \overrightarrow{AB} = mg AB \cos (\alpha) \]
où AB représente la longueur du segment \([A,B]\).
Or, en utilisant les formules de trigonométrie, on obtient le résultat suivant: \(\cos(\alpha) = \frac{z_a - z_b}{AB}\)
On en déduit finalement l'expression du travail du poids ( à connaître !) :
\[ W(\vec{P}) = mg(z_a - z_b) \]
Donc, le travail est moteur si le point A est à une altitude plus importante que le point B et résistant sinon.
On remarque ici que le travail du poids ne dépend pas de la trajectoire suivie par le mobile mais seulement des points de départ et d'arrivée. Cette observation mène alors à l'introduction de la notion de forces conservatives (section 3.1).
2. Théorème de l'énergie cinétique
Théorème 1. (Théorème de l'énergie cinétique)
Considérons un système soumis à n forces quelconques \(\vec{F_1}, ... , \vec{F_n}\), lors d'un déplacement entre les points A et B. Alors, la variation d'énergie cinétique entre A et B, noté \(\Delta_{A \to B} E_c\) vérifie :
Ce résultat est important et découle directement du PFD, on pourra donc l'utiliser à la place de ce dernier et cela pourra avoir de nombreux avantages (cf. TD associé).
Il nous faut maintenant généraliser ce résultat en prenant en compte l'énergie total du système permettant le mouvement (on n'exclut donc l'énergie thermique par exemple). Pour cela, il faut considérer une nouvelle forme d'énergie : l'énergie potentielle.
3. Forces conservatives et énergies potentielles
3.1. Forces conservatives
Définition 2. (Forces conservatives)
On appelle force conservative toute force dont son travail, lors d'un déplacement quelconque, ne dépend pas de la trajectoire. Si l'on considère deux chemins \(C_1\) et \(C_2\) comme ci-dessus :
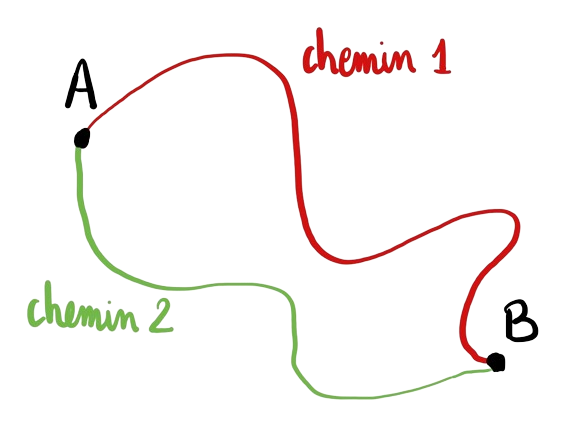
Alors, le travail est invariant dans les deux cas.
Exemple.
- Force conservative : Le poids
- Force non-conservative. En terminale, les seules forces non-conservatives considérées seront les forces de frottements
3.2. Énergie potentielle
Définition 3. (Énergie potentielle)
L'énergie potentielle, généralement notée \(E_p\) dérive d'une force conservative. Elle correspond à la partie d'énergie, possédé par un système, pouvant être convertie en une autre forme d'énergie.
Explication hors-programme : Comme \(E_p\) dérive d'une force \(\vec{F}\) conservative (i.e. vérifie une équation de la forme \(dE_p = - \vec{F} \cdot d\vec{x}\), avec d\(\vec{x}\) un petit déplacement), alors on peut montrer le résultat suivant :
Lien entre travail et énergie potentielle.
La variation d'énergie potentielle d'un système entre A et B vérifie : \[ \Delta_{A \to B} E_p = -W_{AB}\left(\vec{F}\right) \]
Exemple. Expression de l'énergie potentielle de pesanteur (= poids) : \(E_{pp} = mgz\), où z correspond à la variation d'altitude.
On a donc réussi à décrire toutes les énergies permettant à un système le mouvement.
4. Théorème de l'énergie mécanique
Définition 4. (Énergie mécanique)
On définit l'énergie mécanique, noté \(E_m\), comme la somme de l'énergie cinétique \(E_c\) et de l'énergie potentielle \(E_p\). Autrement dit :
On rappelle ici que l'énergie cinétique d'un système vaut \(\frac{1}{2} m v^2\) et que l'énergie potentielle dépend de la configuration du système.
Théorème 2. (Théorème de l'énergie mécanique)
En partant du théorème 1, on montre que la variation d'énergie mécanique d'un système entre A et B vérifie (pour un système soumis à n forces non conservatives) :