Terminale : Exercices sur l'électrocinétique
La mention ❤️ indique que la méthode de résolution proposée par l'exercice est à maîtriser et à savoir refaire, on peut aussi parler d'exercice classique. Finalement, chaque exercice possède sa propre difficulté : 🌶️ pour un exercice facile, 🌶️🌶️ pour un exercice de difficulté moyenne et 🌶️🌶️🌶️ pour un exercice difficile dans sa résolution.
Exercices d'application
Exercice n°1 (Mesure expérimentale d'une capacité lors de la charge) ❤️ 🌶️ 🌶️ 🌶️
On considère un circuit RC série possédant un générateur de force électromotrice \(E\).
1. On cherche dans cette question à relever la tension notée \(u_c\) du condensateur de capacité \(C\) au cours du temps. Quel outil peut-on utiliser ? Dessiner le circuit RC série en incluant le générateur et l'instrument de mesure choisi.
On donne le tableau de mesure suivant :

où \(t\) est donné en secondes.
2. En déduire la capacité \(C\) du condensateur étudié.
Données. \(R=10\) k\(\Omega\).
Voir l'indice
Pour trouver \(\tau\), vous pouvez utiliser deux méthodes : la méthode de la tangente à l'origine (l'abscisse de l'intersection de la tangente avec l'asymptote \(y=E\)) ou la méthode des 63% (le temps au bout duquel \(u_c(t) = 0,63 \times E\)). Essayez de voir si les deux donnent un résultat cohérent.
Afficher le corrigé
1. On utilise un voltmètre. Le cicruit ainsi réalisé ressemble à :
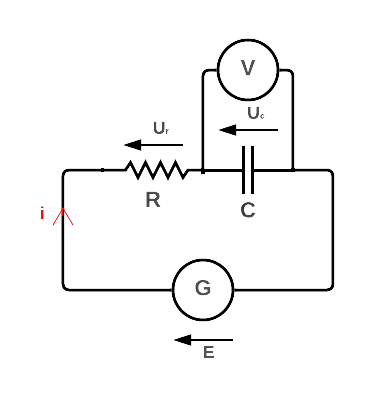
2. Dans ce genre de question, il faut rapidement identifier une démarche de résolution. On connaît deux relations fondamentales mettant en jeu la capacité \(C\) :
\[ q(t)=Cu_c(t)\quad et \quad \tau=RC \]On a aucun accès au tableau de valeurs de \(q\) donc on doit se tourner vers la seconde relation. Ici, \(R\), étant déjà fourni, il faut trouver \(\tau\). Pour s'y prendre, on va devoir raisonner graphiquement. Traçons \(u_c\) en fonction de \(t\).
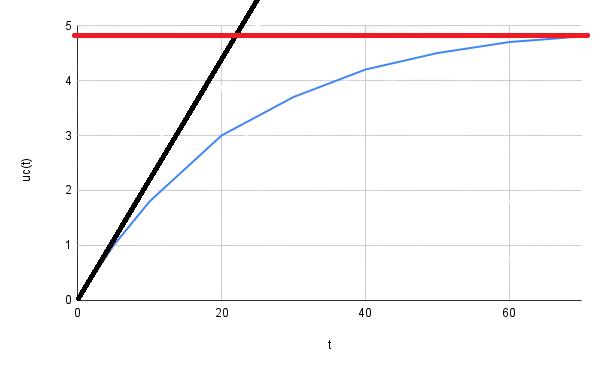
En bleue a été représenté le graphe de la fonction \(u_c\). En noir a été traçé la tangente à l'origine et en rouge la droite d'équation \(y=\lim\limits_{t \rightarrow +\infty} u_c(t)=4,8\) V (la valeur de cette limite est approximative). D'après le cours, on peut récupèrer la valeur \(\tau\) en déterminant l'abscisse du point d'intersection entre les courbes noire et rouge. Graphiquement, on lit \(\tau=22\) s.
\(2^{ème}\) réponse possible pour trouver \(\tau\) : D'après le cours, on sait qu'à \(t=\tau\), \(u_c(\tau)=0,63E\) où \(E=4,8\) V. En faisant la calcul, on obtient que \(u_c(\tau)=3,024\) V. En se référant au tableau, on en déduit approximativement que : \(\tau=20\) s.
Comme \(C=\frac{\tau}{R}\) et que l'on connaît \(R\), on en déduit : \(C=2,2\) mF.
Exercice n°2 (Application des lois des mailles et des nœuds) ❤️ 🌶️ 🌶️ 🌶️
1. Calculer la valeur des tensions algébriques manquantes :
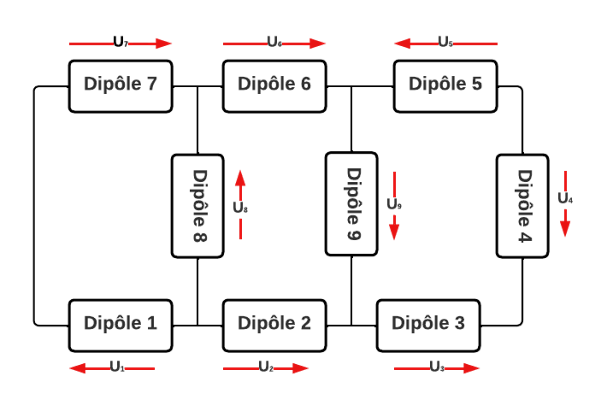
Données. \(u_1=5\) V, \(u_2=4\) V, \(u_3=-3\) V, \(u_4=6\) V, \(u_9=12\) V, \(u_6=-2\) V.
2. Calculer les intensités algébriques dans cette configuration :
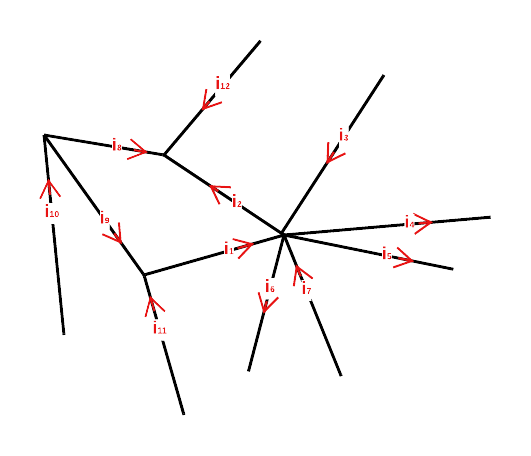
Données. \(i_1=5\) A, \(i_9=4\) A, \(i_{10}=-7\) A, \(i_{12}=6\) A, \(i_3=12\) A, \(i_6=-2\) A, \(i_7=-1\) A, \(i_5=4\) A.
Voir l'indice
Tensions (Loi des mailles) : Faites attention au sens des flèches. Si vous parcourez la maille dans un sens et qu'une flèche de tension est dans le même sens, comptez-la positivement (\(+\)u), sinon négativement (\(-\)u). La somme doit valoir 0.
Intensités (Loi des nœuds) : La somme des courants qui entrent dans un nœud est égale à la somme des courants qui en sortent.
Afficher le corrigé
1. Il suffit d'appliquer la loi des mailles dont chacune des trois mailles du circuit.
Dans la première maille, on écrit : \[ u_1+u_7-u_8=0 \quad (1) \]
Dans la seconde maille, on écrit : \[ u_6+u_9+u_8-u_2=0 \quad (2) \]
Dans la troisième maille, on écrit : \[ u_5+u_9+u_3-u_4=0 \quad (3) \]
L'équation (3) nous permet d'accéder à la valeur de \(u_5\) : \(\boxed{u_5=-3 \text{ V}}\). L'équation (2) nous permet d'accéder à la valeur de \(u_8\) : \(\boxed{u_8=-6 \text{ V}}\). L'équation (1) nous permet d'accéder à la valeur de \(u_7\) : \(\boxed{u_7=-11 \text{ V}}\).
2. On note \(N_1\), \(N_2\), \(N_3\) et \(N_4\) les nœuds suivants :
.png)
Ici, il suffit d'appliquer la loi des noeuds en les 4 nœuds \(N_1\), \(N_2\), \(N_3\) et \(N_4\) :
Au nœud 1, on écrit : \[ i_1=i_9+i_{11} \quad (1) \]
Au nœud 2, on écrit : \[ i_{10}=i_8+i_9 \quad (2) \]
Au nœud 3, on écrit : \[ i_2+i_8+i_{12}=0 \quad (3) \]
Au nœud 4, on écrit : \[ i_1+i_3+i_7=i_2+i_4+i_5+i_6 \quad (4) \]
L'équation (1) nous permet d'obtenir \(\boxed{i_{11}=1 \text{ A}}\). L'équation (2) nous permet d'obtenir \(\boxed{i_{8}=-11 \text{ A}}\). L'équation (3) nous permet d'obtenir \(\boxed{i_{2}=5 \text{ A}}\). L'équation (4) nous permet d'obtenir \(\boxed{i_{4}=9 \text{ A}}\).
Exercice n°3 (Expression de la charge \(q\) dans un circuit électrique) 🌶️ 🌶️ 🌶️
On considère un circuit RC série contenant un générateur de force électromotrice \(E\). On étudie dans cet exercice la charge du condensateur de capacité \(C\).
1. Etablir l'équation différentielle portée sur la tension du condensateur notée \(u_c\).
2. Résoudre cette équation différentielle en exploitant la valeur initale de \(u_c\).
3. En déduire l'expression de l'intensité du courant notée \(i\).
4. Rappeler la relation liant \(i\) à la charge du circuit \(q\).
5. En déduire l'expression de la charge \(q\).
6. En reprenant le circuit, montrer que \(q\) vérifiait l'équation différentielle suivante : \[ \frac{dq(t)}{dt}+\frac{q(t)}{\tau}=\frac{E}{R} \quad (1) \]
7. Vérifier que l'expression de \(q\) obtenue en question 5 est solution de (1).
Voir l'indice
Cet exercice montre que l'on peut décrire le circuit avec \(u_c\) ou \(q\).
Pour la Q5, le plus simple est d'utiliser la relation fondamentale \(\boxed{q(t) = C \times u_c(t)}\) avec le résultat de la Q2.
Pour la Q6, partez de l'équation de la Q1 et remplacez \(u_c\) par \(\frac{q}{C}\) et \(\frac{du_c}{dt}\) par \(\frac{1}{C}\frac{dq}{dt}\).
Afficher le corrigé
1. L'équation différentielle a déjà été établi dans le cours d'électrocinétique : \[ \frac{du_c(t)}{dt}+\frac{u_c(t)}{\tau}=\frac{E}{\tau} \quad (\dagger) \] où \(\tau=RC\).
2. On rappelle que : \(\boxed{u_c(0)=0}\) lors de la charge. D'après le cours, (\(\dagger\)) est une équation différentielle linéaire normalisée du premier ordre à second terme constant. La solution générale est de la forme :
\[ u_c(t)=C^{ste}exp\left(-\frac{t}{\tau}\right)+E \]
où \(C^{ste}\) est une constante réelle.
D'après la condition initiale, on en déduit que : \(\boxed{C^{ste}=-E}\). D'où :
\[ u_c(t)=E\left(1-exp\left(-\frac{t}{\tau}\right)\right) \]
3. Par définition, on a : \[ i(t)=i_c(t)=C\frac{du_c(t)}{dt} \] Ainsi, par dérivation, on en déduit : \[ i_c(t)=\frac{E}{R}exp\left(-\frac{t}{\tau}\right) \]
4. D'après le cours, on a : \[ i(t)=\frac{dq(t)}{dt} \]
5. Retournons l'expression de la question 4 et exprimons \(q\) en fonction de \(i\). Il suffit de primitiver la relation précédente : \[ q(t)=\int i(t)dt \] Soit on primitive \(i\) et on en déduit \(q\) ou soit ou utilise l'égalité suivante : \[ q(t)=Cu_c(t) \] Ainsi, on en déduit immédiatement : \[ q(t)=EC\left(1-exp\left(-\frac{t}{\tau}\right)\right) \]
6. Comme \(u_c\) vérifie l'équation : \[ \frac{du_c(t)}{dt}+\frac{u_c(t)}{\tau}=\frac{E}{\tau} \quad (\dagger) \] De plus, \(q(t)=Cu_c(t)\) et \(\frac{du_c(t)}{dt}=\frac{1}{C}\frac{dq(t)}{dt}\). On en déduit que \(q\) vérifie l'équation différentielle donnée : \[ \frac{dq(t)}{dt}+\frac{q(t)}{\tau}=\frac{E}{R} \]
7. L'expression de \(q\) trouvée en question 5 vérifie bien l'équation de la question 6.
En route vers le supérieur
Exercice n°4 (Energie emmagasinée par un condensateur) ❤️ 🌶️ 🌶️ 🌶️
1. Rappeler l'expression de l'intensité aux bornes d'un condensateur \(i_c\).
2. Rappeler l'expression de la puissance électrique d'un dipôle traversée par un courant \(i\) et possédant une tension aux bornes notée \(u\).
3. Calculer la puissance électrique d'un condensateur notée \(P_c\). Cette puissance est-elle une fonction du temps ? Justifier.
On rappelle que par définition, une puissance dérive d'une énergie. En notant \(E(t)\) l'énergie d'un dipôle électrique et \(P(t)\) sa puissance électrique alors on en déduit la relation suivante : \[ P(t)=\frac{dE(t)}{dt} \] On remarquera que la puissance et l'énergie sont des fonctions du temps.
4. Déterminer l'expression de l'énergie électrique emmagasinée par le condensateur notée \(E_c\). L'énergie \(E_c\) est-elle une fonction du temps ? Justifier.
5. En utilisant un argument physique sur l'énergie \(E_c\), montrer que la tension \(u_c\) est nécessairement une fonction continue au cours du temps.
Voir l'indice (Aide mathématique)
Aide mathématique pour la question 4 :
Soit \(f\) une fonction de dérivée continue alors la dérivée de \(f^2\) est donnée par la formule suivante : \[ \forall t>0, \quad \frac{d\left(f^2(t)\right)}{dt}=2f'(t)f(t) \] Réciproquement, on peut écrire : \[ \int_{}^{} f'(t)f(t) \, \mathrm{d}t=\frac{1}{2}f^2(t) \] Ces deux écritures sont équivalentes.
Afficher le corrigé
1. D'après le cours, on a : \[ i_c(t)=C\frac{du_c(t)}{dt} \]
2. On définit la puissance électrique \(P\) comme : \[ \boxed{P=ui} \]
3. Il suffit de développer la réponse de la question 2 : \[ \begin{align*} P_c &= u_c(t)i_c(t)\\ P_c &= u_c(t)\left(C\frac{du_c(t)}{dt}\right)\\ P_c &= Cu_c(t)\frac{du_c(t)}{dt} \end{align*} \] \(P_c\) est bien sûr une fonction du temps car en régime variable, \(u_c\) et \(i\) varient avec le temps.
4. Il faut utiliser l'aide mathématique, on doit chercher à écrire \(P_c\) comme la dérivée d'une énergie qu'on note \(E_c\). L'astuce est de remarquer que : \[ \frac{du_c^2(t)}{dt}=2u_c(t)\frac{du_c(t)}{dt} \] On poursuit alors les calculs de la question 3 : \[ \begin{align*} P_c &= Cu_c(t)\frac{du_c(t)}{dt}\\ P_c &= \frac{1}{2}C\frac{du_c^2(t)}{dt}\\ P_c &= \frac{d\left(\frac{1}{2}Cu_c^2(t)\right)}{dt} \end{align*} \] On pose alors : \(\boxed{E_c(t)=\frac{1}{2}Cu_c^2(t)}\). Cette énergie correspond à l'énergie emmagasinée au sein du condensateur.
5. L'énergie est une grandeur physique continue. En effet, une discontinuité de l'énergie n'est pas envisable dans la vraie vie à cause des principes de conservation de l'énergie. Comme \(E_c\) est continue, d'après son expression, on en déduit que \(\boxed{u_c \text{ est continue}}\).
Exercice n°5 (Résistance équivalente en série et en dérivation) ❤️ 🌶️ 🌶️ 🌶️
L'objectif de cet exercice est de savoir quelle résistance faut-il prendre pour remplacer deux résistances en série et en dérivation.
On considère, dans le suite de l'exercice, deux résistances, la première notée 1 de résistance \(R_1\) et la seconde notée 2 de résistance \(R_2\). D'autre part, on considère une autre résistance notée 0 de résistance \(R_0\).
1. On place les résistances 1 et 2 en série. On cherche l'expression de \(R_0\) telle que le système {1+2} équivaut au système {0}.
En utilisant la loi des mailles, montrer la relation suivante :
\[ R_0=R_1+R_2 \]
2. On place les résistances 1 et 2 en dérivation. On cherche l'expression de \(R_0\) telle que le système {1+2} équivaut au système {0}.
2.1. En utilisant la loi des nœuds, établir l'égalité : \[ \frac{u_{r_0}}{R_0}=\frac{u_{r_1}}{R_1}+\frac{u_{r_2}}{R_2} \] où \(u_{r_k}\) est la tension aux bornes de la résistance k.
2.2. En utilisant la loi des mailles, montrer la relation suivante : \[ \frac{1}{R_0}=\frac{1}{R_1}+\frac{1}{R_2} \]
Voir l'indice
Pour la série : Le courant \(i\) qui traverse les deux résistances est le même (\(i_0=i_1=i_2\)). Les tensions s'ajoutent : \(u_0 = u_1 + u_2\).
Pour la dérivation : La tension \(u\) aux bornes des deux résistances est la même (\(u_0 = u_1 = u_2\)). Les courants s'ajoutent : \(i_0 = i_1 + i_2\).
Afficher le corrigé
1. On se place dans la configuration suivante :
.png)
D'après la loi des mailles, on peut écrire : \[ u_{r_0}=u_{r_1}+u_{r_2} \] D'après la loi d'Ohm, on en déduit : \[ R_0i=R_1i+R_2i \] En simpliant par \(i\), il en résulte que : \[ \boxed{R_0=R_1+R_2} \]
2. On se place dans la configuration suivante :
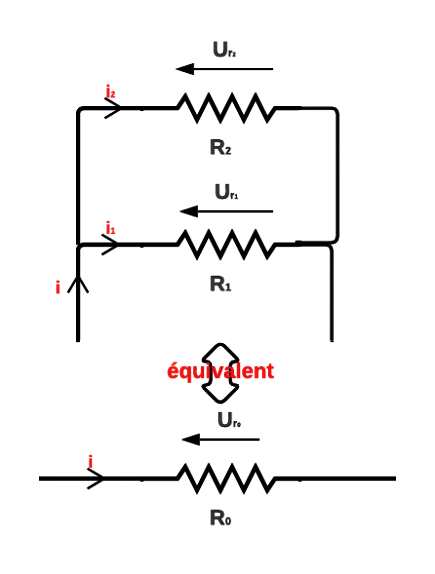
2.1. C'est une conséquence directe de la loi des nœuds : \[ i=i_1+i_2 \] D'après la loi d'Ohm, il en suit que : \[ \frac{u_{r_0}}{R_0}=\frac{u_{r_1}}{R_1}+\frac{u_{r_2}}{R_2} \]
2.2. La loi des mailles nous permet d'écrire l'égalité suivante : \[ u_{r_0}=u_{r_1}=u_{r_2} \] En écrivant avec la réponse précédente le résultat de la question 2.1, on déduit : \[ \frac{u_{r_0}}{R_0}=\frac{u_{r_0}}{R_1}+\frac{u_{r_0}}{R_2} \] En simplifiant par \(u_{r_0}\), on démontre que : \[ \boxed{\frac{1}{R_0}=\frac{1}{R_1}+\frac{1}{R_2}} \]
Exercice n°6 (Condensateur équivalent en série et en dérivation) ❤️ 🌶️ 🌶️ 🌶️
L'objectif de cet exercice est de savoir quel condensateur faut-il prendre pour remplacer deux condensateurs en série et en dérivation.
On considère, dans le suite de l'exercice, deux condensateurs, le premier noté 1 de capacité \(C_1\) et le second noté 2 de capacité \(C_2\). D'autre part, on considère un autre condensateur noté 0 de capacité \(C_0\).
1. On place les condensateurs 1 et 2 en série. On cherche l'expression de \(C_0\) telle que le système {1+2} équivaut au système {0}.
1.1. Justifier l'égalité suivante : \[ C_0u_{c_0}=C_1u_{c_1}=C_2u_{c_2} \] où \(u_{c_k}\) représente la tension aux bornes du condensateur k.
1.2. En utilisant la loi des mailles, montrer la relation suivante : \[ \frac{1}{C_0}=\frac{1}{C_1}+\frac{1}{C_2} \]
2. On place les condensateurs 1 et 2 en dérivation. On cherche l'expression de \(C_0\) telle que le système {1+2} équivaut au système {0}.
2.1. Justifier par un argument sur la charge \(q\) de la maille principale la relation suivante : \[ C_0u_0=C_1u_{c_1}+C_2u_{c_2} \]
2.2. En utilisant la loi des mailles, montrer la relation suivante : \[ C_0=C_1+C_2 \]
Voir l'indice
Attention, les règles pour les condensateurs sont l'inverse de celles des résistances !
Pour la série : La charge \(q\) sur chaque condensateur est la même (\(q_0 = q_1 = q_2\)). Les tensions s'ajoutent : \(u_0 = u_1 + u_2\).
Pour la dérivation : La tension \(u\) aux bornes des deux condensateurs est la même (\(u_0 = u_1 = u_2\)). Les charges s'ajoutent : \(q_0 = q_1 + q_2\).
Afficher le corrigé
On raisonne comme dans l'exercice précédent.
1. On se place dans la configuration suivante :
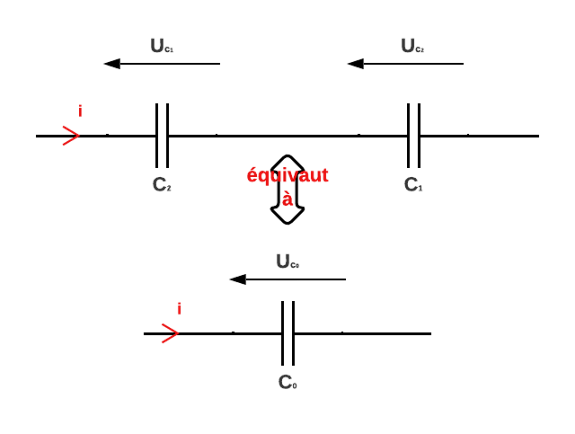
1.1. Notons \(q\) la charge qui passe à travers une section de fil qu'on suppose égale en tout point du circuit (hypothèse évoquée dans le cours). Or cette charge \(q\) est la même aux condensateurs 0, 1 et 2 car l'intensité est la même en ces points. On a l'égalité : \[ q_0=q_1=q_2 \] D'après le cours, on en déduit que : \[ C_0u_{c_0}=C_1u_{c_1}=C_2u_{c_2} \]
1.2. La loi de mailles nous permet d'écrire la relation : \[ u_{c_0}=u_{c_1}+u_{c_2} \] En injectant cette relation dans celle obtenue à la question 1.1, on trouve : \[ C_0\left(u_{c_1}+u_{c_2}\right)=C_1u_{c_1} \] Or, on peut exprimer \(u_{c_2}\) en fonction de \(u_{c_1}\) par la relation : \[ u_{c_2}=\frac{C_1}{C_2}u_{c_1} \] En regroupant toutes ces équations, on en déduit que : \[ C_0\left(u_{c_1}+\frac{C_1}{C_2}u_{c_1}\right)=C_1u_{c_1} \] Il suffit maintenant de simpliquer par \(u_{c_1}\) : \[ C_0\left(1+\frac{C_1}{C_2}\right)=C_1 \] En isolant \(C_0\), on en conclut que : \[ \boxed{\frac{1}{C_0}=\frac{1}{C_1}+\frac{1}{C_2}} \]
2. La configuration adoptée maintenant est la suivante :
.png)
2.1. Ici, il suffit de comprendre que la charge est une grandeur additive. En effet, on peut appliquer une loi des nœuds adaptée à la charge \(q\) : \[ q_0=q_1+q_2 \] D'après la relation du cours liant la charge à la tension du condensateur, on a : \[ C_0u_0=C_1u_{c_1}+C_2u_{c_2} \]
2.2. La loi des mailles permet de justifier l'égalité : \[ u_{c_0}=u_{c_1}=u_{c_2} \] Ainsi, on peut réecrire le résultat de la question précédente : \[ C_0u_0=C_1u_{c_0}+C_2u_{c_0} \] En simplifiant par \(u_{c_0}\), on peut conclure : \[ \fbox{C_0=C_1+C_2} \]
Exercice n°7 (BAC Centres étrangers 2022) 🌶️ 🌶️ 🌶️
L'intérêt de sujet est d'observer quelques utilisations pratiques d'un condensateur.
I. La balance capacitive
Dans la vie quotidienne, certaines balances électroniques utilisent un capteur à capacité variable afin de mesurer la masse des objets. Pour comprendre le fonctionnement d’un tel dispositif, on envisage dans cette partie une modélisation très simplifiée dans laquelle la balance est modélisée par un condensateur comportant une armature mobile reliée au plateau de pesée et une armature fixe reliée au support de la balance.
On modélise simplement une balance de laboratoire :

Lorsque la balance est à vide (sans masse sur le plateau), la distance entre les deux armatures est notée \(e_0\). Lorsqu’un objet de masse \(M\) est posé sur le plateau de pesée, les armatures du condensateur se rapprochent, modifiant alors la valeur de sa capacité \(C\). Les deux armatures ne peuvent pas entrer en contact grâce à la présence de petites butées de taille négligeable devant \(e_0\). La mesure de la capacité \(C\) par un dispositif électronique permet alors de déterminer la masse \(M\) de l’objet.

On pourrait montrer mais on l'admet que la capacité \(C\) du condensateur dépend de la géométrie du condensateur et des caractéristiques du milieu isolant choisi entre les armatures : \[ C=\frac{\epsilon_0\epsilon_rS}{e} \quad (2) \] \(S\) représente la surface des armatures, \(\epsilon_0\) la permitivité diélectrique du vide valant \(8,85.10^{-12}\) F.m⁻¹, \(\epsilon_r\) la permitivité diélectrique relative à l'isolant choisi valant 1 pour l'air et le vide, \(e\) représente la distance entre les deux armatures et on prend comme référence \(e_0=1\) m.
1. Domaine d'utilisation de la balance
1.1. Calculer la valeur de la capacité du condensateur à vide notée \(C_0\).
1.2. Qualitativement, expliquer comment varie la capacité \(C\) lorsqu'on place une masse sur le plateau de la balance.
On suppose que si on place un objet de masse \(M\) sur le plateau de la balance, le support passe d'une distance \(D_0\) à une distance \(D\) grâce à l'action d'une force \(\vec{F}\) dirigée vers le haut dont la norme est donnée par l'expression : \[ \left\|\vec{F}\right\|=k\left(D_0-D\right) \quad (3) \] avec \(k=980\) N.m⁻¹.
1.3.1. Montrer que si l'on pose un objet de masse \(M\) sur la balance, connaissant la distance entre le support et le plateau notée \(D\), on peut écrire : \[ M=\frac{k}{g}\left(D_0-D\right) \quad (4) \] avec \(g=9,81\) N.kg⁻¹.
1.3.2. On admet que l'armature du condensateur se déplace de la même distance que le plateau lorsqu'on y pose un objet de masse \(M\). Montrer qu'il existe une masse maximale notée \(M_{max}\) que peut mesurer la balance à déterminer en fonction des données de l'énoncé.
2. Mesure de la masse à peser
Pour déterminer la valeur de la capacité \(C\) du condensateur et en déduire la valeur de la masse immobile sur le plateau, on étudie la charge du condensateur à partir du circuit ci-dessous. À l’instant \(t = 0\), le condensateur est déchargé ; on applique alors au circuit la tension \(E\).
2.1. Déterminer l'équation différentielle vérifiée par \(u_c\) dans le circuit suivant :
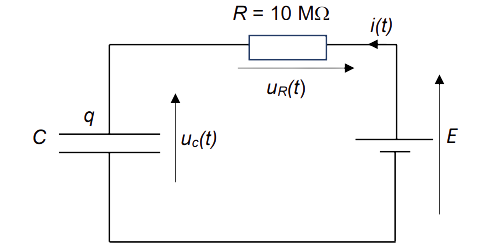
2.2. Définir une constante de temps notée \(\tau\) en fonction de \(R\) et \(C\).
2.3. Rappeler une condition initale vérifiée \(u_c\) dans ce cas en la justifiant.
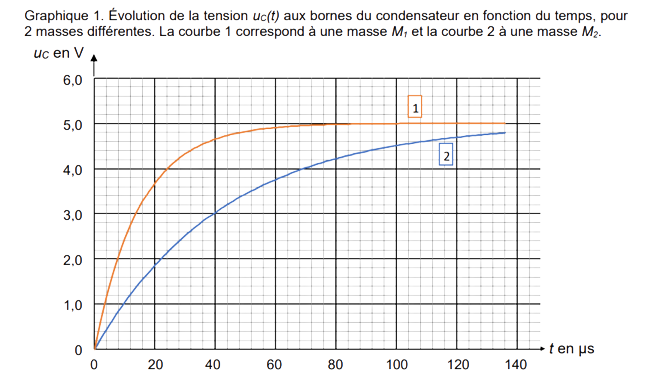
2.4. En déduire que \(u_c\) se met sous la forme suivante : \[ u_c(t)=E\left(1-exp\left(-\frac{t}{\tau}\right)\right) \quad (5) \] En annexe est fourni deux graphes 1 et 2 présentant la mesure de la tension \(u_c\) au cours du temps pour deux masses distinctes \(M_1\) et \(M_2\).
2.5. Déterminer quel graphe correspond à une grande valeur de capacité \(C\) en justifiant votre réponse.
2.6. En s'aidant des graphes 1 et 2 fournis, déterminer la valeur de la masse \(M_2\). La méthode utilisée devra être présentée et justifiée.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.
Annexe de l'exercice :
Voir l'indice
C'est un problème de synthèse. La clé est de chaîner les relations :
- Relier la masse \(M\) à la distance \(D\) (ou \(e\)) grâce au PFD (Q 1.3.1).
- Relier la distance \(e\) à la capacité \(C\) (Q 1.2 / Éq. 2).
- Relier la capacité \(C\) au temps \(\tau\) (Q 2.2).
- Trouver \(\tau\) sur le graphe (Q 2.6) en utilisant la méthode des 63%.
- Remonter la chaîne : \(\tau_2 \rightarrow C_2 \rightarrow e_2 \rightarrow M_2\).
Afficher le corrigé
1.1. Il suffit d'utiliser la relation (2) et d'en faire l'application numérique (point de vigilance : ici, les données de l'énoncé ne sont pas toutes dans les unités du système international des unités !) On rappelle que 1 cm² est égal à \(10^{-4}\) m². On en déduit que : \(C_0=\frac{\epsilon_0\epsilon_rlL}{e_0}\) = 1,06.\(10^{-14}\) F.
1.2. Lorsque une masse est posée sur le plateau, il en suit que la distance entre le plateau et l'armature fixe diminue donc la valeur de \(e\). Dans notre cas, \(C\) est inversement proportionnel à \(e\) donc \(C\) croît dans ce cas.
1.3.1. Pour effectuer la mesure de la masse, on attend l'équilibre du plateau. A cette étape, la vitesse du plateau relativement au référentiel terrestre est nulle. Il en résulte que son accélération est nulle. En appliquant le principe fondamental de la dynamique à notre système {Plateau} dans le référentiel terrestre alors il en suit que : \[ \boxed{\vec{0}=\vec{F}+M\vec{g}} \] où la masse du plateau est négligée par rapport à la masse \(M\).
En projetant nos vecteurs \(\vec{F}\) et \(\vec{g}\) dans le plan, (même direction mais sens opposé), la relation devient : \[ 0=\left\|\vec{F}\right\|=k\left(D_0-D\right)-Mg \] D'où la relation demandée : \[ \boxed{M=\frac{k}{g}\left(D_0-D\right)} \]
1.3.2. La différence \(\left(D_0-D\right)\) est bornée entre 0 quand \(D=D_0\) et \(D_0\) quand \(D=0\). Or on fait l'hypothèse que le plateau est fixé à l'armature mobile donc ils se déplacent depuis la même distance initiale d'où \(D_0=e_0\). La masse maximale \(M_{max}\) qu'on peut mesurer est celle qui amenera le plateau à \(D=0\), d'où : \[ \boxed{M_{max}=\frac{k}{g}e_0} \]
2.1. L'équation différentielle a déjà été établi dans le cours d'électrocinétique : \[ \frac{du_c(t)}{dt}+\frac{u_c(t)}{RC}=\frac{E}{RC} \]
2.2. On pose comme constante de temps notée \(\tau\) la valeur : \[ \tau=RC \]
2.3. On rappelle que : \(\boxed{u_c(0)=0}\) lors de la charge. En effet, à \(t=0^-\), la tension est nulle et par continuité, on en déduit que \(u_c(0)=0\).
2.4. D'après le cours, l'équation obtenue est une équation différentielle linéaire normalisée du premier ordre à second terme constant. La solution générale est de la forme :
\[ u_c(t)=C^{ste}exp\left(-\frac{t}{\tau}\right)+E \]
où \(C^{ste}\) est une constante réelle.
D'après la condition initiale, on en déduit que : \(\boxed{C^{ste}=-E}\). D'où :
\[ u_c(t)=E\left(1-exp\left(-\frac{t}{\tau}\right)\right) \]
2.5. Soient \(C_1\) et \(C_2\) deux valeurs de capacités telles que :
\[ \begin{align*}
&\quad C_1
2.6. Ici, on veut déterminer \(M_2\). Si l'on fait l'inventaire des résultats qu'on connaît à ce stade, on sait que :
\[ M_2=\frac{k}{g}\left(e_0-e_2\right) \quad et \quad \tau=RC_2 \]
Graphiquement, on peut récupérer \(\tau\) en sachant pour quelle valeur de \(t\), \(u_c\) (courbe bleue) atteint 63 \% de sa valeur limite qu'on notera \(E\). On peut lire graphiquement que \(E=4,8\) V donc \(u_c(\tau)=3,0\) V. Il en résulte que \(\tau=40\) µs. Comme \(R=10\) M\(\Omega\), on a : \(C_2=4,0.10^{-12}\) F. D'après la relation (3) [Note: il s'agit de la relation (2) dans l'énoncé] de l'énoncé donnant l'expression de \(C_2\), on peut écrire :
\[ \boxed{e_2=\frac{\epsilon_0\epsilon_rS}{C_2}} \]
Par application numérique, on trouve : \(e_2=2,7\) mm. D'après la relation exprimant \(M_2\), on peut conclure : \(M_2=99,63\) kg. Ce résultat est-il crédible ? Regardons ça...
Analysons ce résultat pour achever cet exercice. Les armatures sont passées d'une distance de séparation de 1 m à une distance de quelques millimètres. C'est logique que cette masse soit grande et d'autre part, proche de \(M_{max}\) qui vaut 99,90 kg car \(e_2 \ll e_0\). Cela conclut cet exercice.