Terminale : L'électrocinétique
Dans ce chapitre, nous allons étudier les lois fondamentales de l'électricité en mouvement (l'électrocinétique). Nous nous intéresserons aux lois de base comme la loi des nœuds et la loi des mailles, avant de nous concentrer sur le comportement d'un composant essentiel en régime variable : le condensateur, à travers l'étude du circuit RC série.
📚 Table des matières
1. Premières lois de l'électrocinétique
Définition 1. (Électrocinétique)
L'électrocinétique désigne la branche de l'électricité qui s'intéresse à l'étude des phénomènes propres à l'électricité en mouvement. Elle s'oppose à l'électrostatique.
Théorème 1. (La loi des nœuds)
En un nœud d'un circuit électrique, la somme algébrique des intensités est nulle.
Intéressons nous à un nœud à \(n\) entrées algébriques :
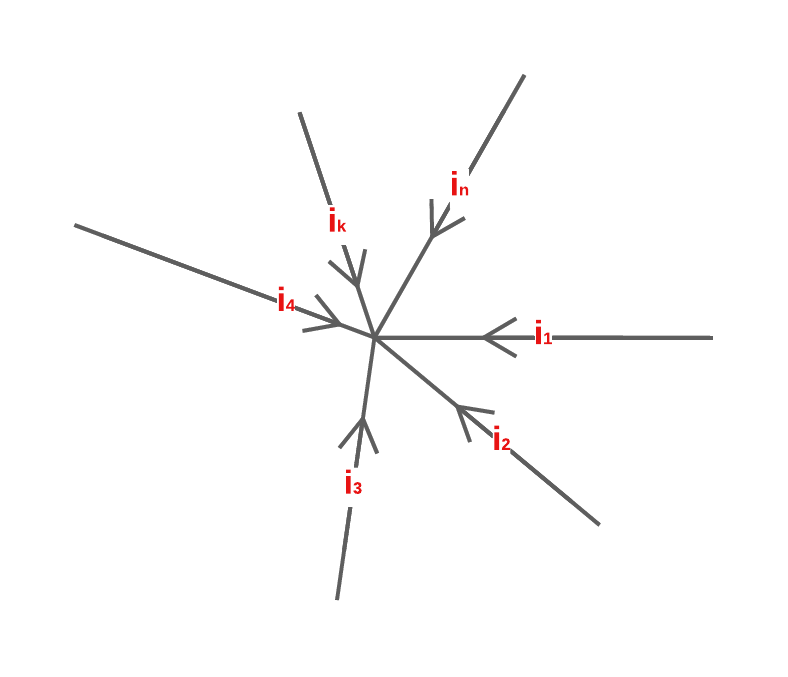
Figure 1. Nœud électrique
Ici, \(\epsilon_k=+1\) lorsque \(i_k\) est une entrée et \(\epsilon_k=-1\) lorsque \(i_k\) est une sortie.
Théorème 2. (La loi des mailles)
Dans un circuit électrique, la somme algébrique des tensions est nulle.
Intéressons nous à un circuit électrique composé de \(n\) dipôles électriques :
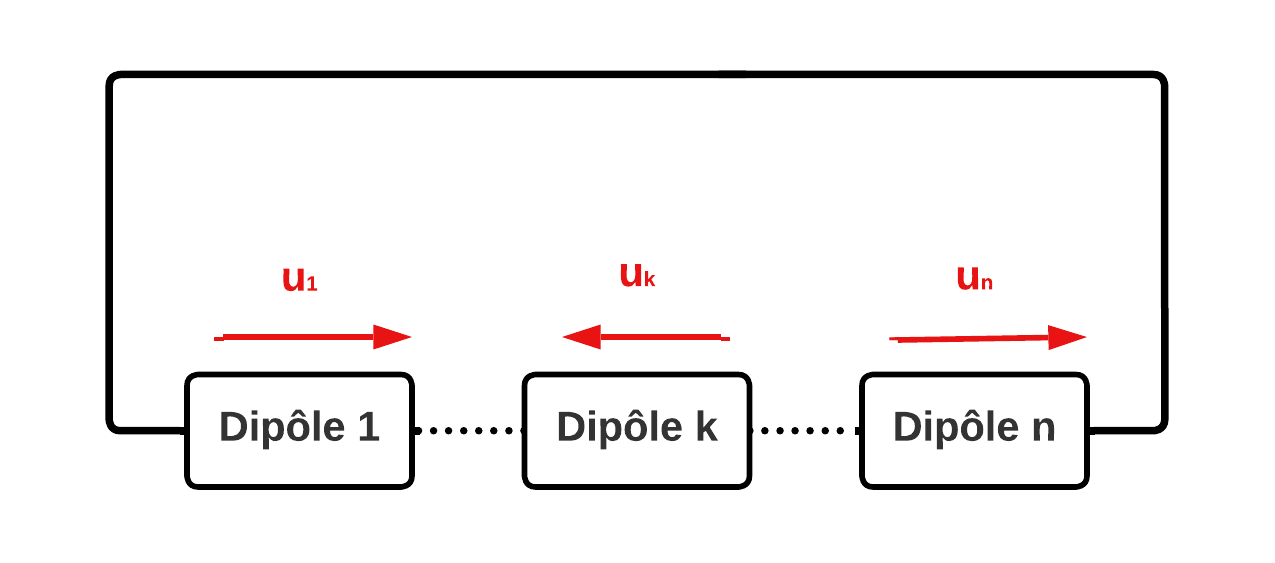
Figure 2. Maille électrique
Ici, \(\epsilon_k=+1\) lorsque \(u_k\) est orientée dans le même sens de lecture de la maille et \(\epsilon_k=-1\) dans le cas contraire.
Remarque : Attention, dans les énoncés précédents, les grandeurs \(i_k\) et \(u_k\) sont algébriques, autrement dit, elles peuvent être positives comme négatives.
Théorème 3. (La loi d'Ohm)
Toute résistance a sa tension qui est proportionnelle à l'intensité du courant qui la traverse.
où \(U\) désigne la tension, \(I\) l'intensité du courant et \(R\) le coefficient de proportionnalité appelé résistance.
Cette loi a été découverte par le physicien allemand Georg Ohm au \(19^e\) siècle. Elle est phénoménologique, c'est-à-dire qu'elle n'a pas de démonstration mathématique mais qu'elle a été prouvée expérimentalement seulement.
2. Le condensateur
Définition 2. (Régime variable)
Un circuit électrique est en régime variable lorsque ses grandeurs caractéristiques varient au cours du temps.
En régime variable, l'intensité du courant et les tensions des dipôles varient au cours du temps.
Définition 3. (Intensité du courant en régime variable)
En régime variable, l'intensité électrique du circuit \(i\) varie au cours du temps, c'est donc une fonction du temps. On pose par définition :
où \(q(t)\) représente le nombre de charges qui traverse une section de fil à l'instant \(t\). On admet (HP) que \(q(t)\) ne dépend pas de la section considérée.
Définition 4. (Le condensateur)
Un condensateur est un dipôle électrique constitué de deux armatures conductrices parallèles séparées par un composant diélectrique, l'équivalent d'un isolant. Lorsqu'il est alimenté par un courant, l'une des plaques accumule des charges positives et l'autre des charges négatives.
Voici le schéma d'un condensateur en électrocinétique :
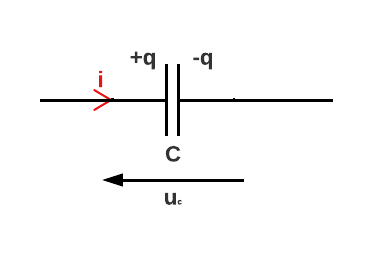
Figure 3. Condensateur en convention récepteur
Cette représentation est vraie lorsque le condensateur est en convention récepteur seulement, nous verrons qu'en convention générateur, l'intensité \(i\) est dirigée dans l'autre sens, du + au -.
Définition 5. (La capacité)
Dans un condensateur, la charge \(q\) d'un condensateur est proportionnelle à sa tension notée \(u_c\). En régime variable, comme \(u_c\) dépend du temps, \(q\) en dépend aussi.
La constante \(C\) s'appelle capacité du condensateur et s'exprime en Farads (F).
On peut donner un sens physique à la constante \(C\). Elle illustre à quel point le condensateur peut stocker des charges sur ses armatures. On parle de pouvoir d'accumulation. Une capacité grande implique un nombre de charges plus grand à la surface des armatures.
On peut montrer (Hors programme) que la capacité dépend de la géométrie du condensateur et des caractéristiques du milieu diélectrique choisi.
Proposition 1. (Intensité aux bornes d'un condensateur)
Aux bornes d'un condensateur, l'intensité notée \(i_c\) s'exprime par la relation suivante :
Preuve
D'après la définition 3, l'intensité aux bornes d'un condensateur s'exprime par la relation : \[i_c(t)=\frac{dq(t)}{dt}\] Or d'après la définition 5, on peut aussi écrire : \[q(t)=Cu_c(t)\] En injectant la seconde relation dans la première, comme \(C\) est une constante, on obtient : \[i_c(t)=\frac{d\left(Cu_c(t)\right)}{dt}=C\frac{du_c(t)}{dt}\] Ce qui achève la preuve.
3. Le circuit RC série : charge du condensateur
3.1 Le schéma du circuit étudié
Dans cette section, on va appliquer tout ce qui a été vu précedemment pour étudier le comportement dynamique d'un circuit électrique : le circuit électrique RC.
Définition 6. (Le circuit RC série)
Le circuit RC série est un circuit d'une seule maille composé d'un générateur de force électromotrice notée \(E\), d'un condensateur de capacité \(C\) et d'une résistance de valeur \(R\).
Voici le schéma du circuit que l'on étudie :
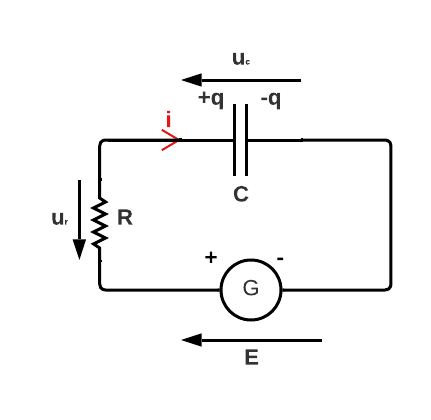
Figure 4. Circuit RC série (charge)
Remarque : A partir de maintenant, on ne fera plus la distinction entre \(i\) et \(i_c\), c'est-à-dire, que : \(i=i_c\).
3.2 Approche dynamique du circuit
L'objectif de cette partie est d'étudier les grandeurs caractéristiques du circuit RC série : l'intensité du courant \(i\) et la tension aux bornes du condensateur \(u_c\).
D'après la proposition 1, si l'on détermine \(u_c\) alors on pourra aussi trouver \(i\). Comment déterminer l'expression de \(u_c\) ? On va chercher à établir une équation où la seule inconnue sera \(u_c\), on verra que cette équation réunira des constantes, \(u_c\) et sa dérivée \(\frac{du_c}{dt}\). On parle d'équation différentielle.
Exercice (À savoir refaire!)
Détermination de l'expression de \(u_c\) et de \(i\)
1. En appliquant la loi des mailles dans le circuit RC étudié, montrer que l'équation différentielle s'écrit :
où \(\tau=RC\).
2. Déterminer l'expression de \(u_c\) sachant que \(u_c(0)=0\).
Correction.
1. Appliquons la loi des mailles dans la figure 4, on obtient donc :
\[u_r(t) + u_c(t) = E\]D'après la loi d'Ohm, on peut écrire :
\[u_r(t) = Ri(t)\]D'autre part, la propositon 1 fournit la relation suivante :
\[i_c(t)=i(t)=C\frac{du_c(t)}{dt}\]En injectant les relations (5) et (6) dans (4), on obtient finalement :
\[RC\frac{du_c(t)}{dt} + u_c(t) = E\]En divisant l'équation (7) par \(\tau=RC\), on en déduit (3) :
\[\frac{du_c(t)}{dt} + \frac{u_c(t)}{\tau} = \frac{E}{\tau}\]2. Ici, on a une équation différentielle linéaire du premier ordre à second membre constant. D'après le cours sur les équations différentielles, on sait que les solutions sont de la forme :
\[y : \mathbb{R^+} \to \mathbb{R}, \quad y(t)=C^{ste}exp\left(-\frac{t}{\tau}\right) + E\]où \(C^{ste}\) désigne une constante. Pour déterminer LA solution qui nous intéresse, on doit déterminer la bonne constante. D'après le cours, trouver la bonne constante se fait en ayant une condition initiale sur \(u_c\). Supposons que \(u_c\) s'écrit :
\[u_c(t)=C^{ste}exp\left(-\frac{t}{\tau}\right)+E\]alors comme \(u_c(0)=0\), on obtient l'implication suivante :
\[C^{ste}+E=0 \Longrightarrow C^{ste}=-E\]On en déduit finalement l'expression de \(u_c\) :
\[u_c(t)=E\left(1-exp\left(-\frac{t}{\tau}\right)\right)\]Proposition 2. (Continuité de la tension \(u_c\))
La tension aux bornes d'un condensateur est continue. En mode récepteur, lorsque le condensateur se charge, on peut écrire : \(u_c(0)=0\).
(La preuve qui suit, celle de la proposition 2, est hors programme. On invite tout de même le lecteur à la lire et à comprendre les idées mises en jeu derrière car elle fait intervenir diverses notions dont celle de continuité en un point.)
Preuve (Hors programme)
On distingue deux instants, \(t=0\) et \(t=0^-\) (instant peu avant \(t=0\)). C'est à \(t=0\) qu'on branche et allume le générateur donc avant, en \(t=0^-\), aucune tension n'était imposée au circuit. Ici le condensateur agit comme un récepteur, il se charge au cours du temps donc quand rien ne lui est imposé à \(t=0^-\), il ne contient pas de charge d'où \(q(t=0^-)=0\). D'après la relation donnée à la définition 5, on en déduit aussi que : \(u_c(t=0^-)=0\).
Comme la tension \(u_c\) est continue car \(u_c\) est dérivable, on a, entre autres, l'égalité :
\[u_c(t=0^-)=u_c(t=0)\]
Cette relation n'est que l'écriture de la définition de la continuité en un point, ici 0. Finalement, c'est comme ça qu'on en déduit que :
\[u_c(0)=0\]
Ce qui achève la preuve.
Définition 7. (Le temps caractéristique du circuit RC série)
On peut définir une grandeur appelée temps caractéristique, notée généralement \(\tau=RC\), telle qu'à cet instant, \(u_c\) a atteint 63\% de sa valeur maximale, \(E\) :
Remarque : Lorsqu'on procéde aux calculs, on peut montrer que : \(u_c(3\tau) \approx 0,95E\). Pour approfondir légèrement, on dit que \(3\tau\) est le temps de réponse à 5\% du circuit et on le note \(\tau_{5\%}\). Ainsi, on a : \(\tau_{5\%}=3\tau\).
Proposition 3. (Expression de la tension \(u_c\))
La tension aux bornes du condensateur s'exprime par la relation :
où \(\tau=RC\).
Preuve
La preuve correspond à toute la correction de l'exercice précédent.
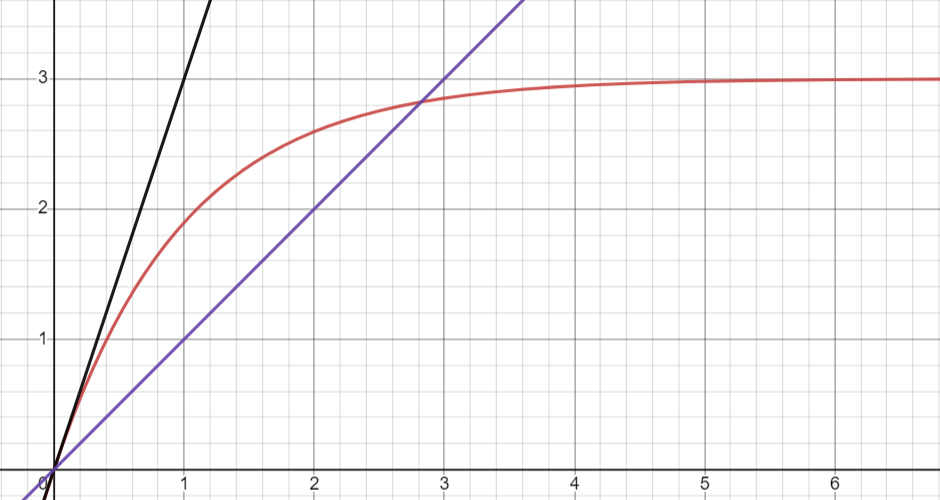
Figure 5. Tracé de \(u_c(t)\) (charge) avec tangente à l'origine
Remarque : (lecture graphique). Lorsque on nous fournit le graphe de la tension \(u_c\), on peut retrouver les valeurs des paramètres \(E\) et \(\tau\). Si l'on trouve \(\tau\) par exemple, connaissant \(R\), on peut en déduire la valeur de \(C\).
Pour retrouver \(E\), il suffit d'observer quelle est la limite de \(u_c\) quand \(t \rightarrow + \infty\).
Pour retrouver \(\tau\), il suffit de tracer en 0 la droite tangente au graphe de la fonction \(u_c\). Ensuite, il faut calculer l'abscisse du point d'intersection entre cette tangente et la droite horizontale d'équation \(y=E\). Cette abscisse est \(\tau\).
C'est ce qu'on peut être amené à faire en TP par exemple.
Proposition 4. (Expression de l'intensité \(i_c\))
L'intensité aux bornes du condensateur s'exprime par la relation :
où \(\tau=RC\).
Preuve
D'après la proposition 1, on peut écrire : \[i_c(t)=C\frac{du_c(t)}{dt}\] Il suffit de dériver l'expression de \(u_c\) donnée dans la proposition 3 pour retrouver celle de \(i_c\). Ainsi, on peut écrire : \[i_c(t)=C\frac{d\left(E\left(1-exp\left(-\frac{t}{\tau}\right)\right)\right)}{dt}=EC\frac{d\left(1-exp\left(-\frac{t}{\tau}\right)\right)}{dt}=\frac{EC}{\tau}exp\left(-\frac{t}{\tau}\right)=\frac{E}{R}exp\left(-\frac{t}{\tau}\right)\] car on rappelle que \(\tau=RC\). Ce qui achève la preuve.
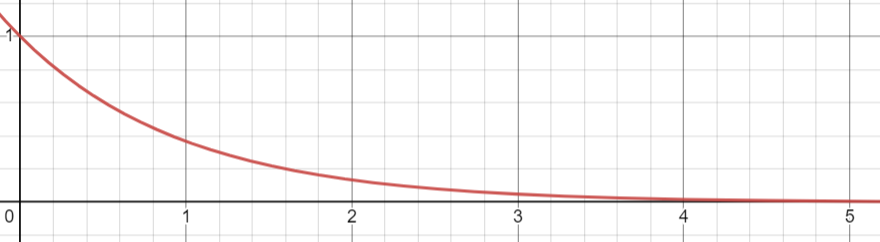
Figure 6. Tracé de \(i_c(t)\) (charge)
Remarque : Les courbes d'intensité sont moins exploitées en pratique mais peuvent être utiles pour connaître la valeur de \(\tau\).
En effet, à l'origine, l'intensité \(i_c(0)\) prend la valeur \(\frac{E}{R}\).
À \(t=\tau\), on peut montrer que l'intensité a perdu 63\% de sa valeur initiale pour ne valoir, à cet instant, que \(0,37\frac{E}{R}\). Ainsi, on cherche graphiquement à quel instant \(t\), \(i_c(t) \approx 0,37 \times i_c(0)\). On aura alors : \(t=\tau\).
4. Le circuit RC série : décharge du condensateur
4.1 Le schéma du circuit étudié
Dans cette section, on étudie une autre forme de circuit RC série. Le condensateur est un dipôle qui est à la fois un récepteur (partie 3), mais aussi un générateur. En effet, un condensateur se charge comme on pourrait charger une pile et lorsqu'il est chargé, on peut l'utiliser pour qu'il délivre tout ce qu'il a accumulé.
Ainsi, le condensateur peut aussi jouer le rôle de générateur lorsqu'il est chargé. C'est l'objet d'étude de cette nouvelle partie.
Remarque : Dans le schéma qui suit, on intègre deux mailles. Une qui permet au condensateur de se charger (interrupteur \(K_1\)) et d'atteindre une tension \(E\). Une autre où le condensateur se décharge dans une résistance (interrupteur \(K_2\)).
D'abord on ferme \(K_1\) (et \(K_2\) ouvert), le condensateur se charge. Dans un second temps, lorsqu'il est complètement chargé, on ouvre \(K_1\) et on ferme \(K_2\), c'est ce qui assure la décharge.
Voici le schéma du circuit que l'on étudie (on considère \(K_1\) ouvert et \(K_2\) fermé) :
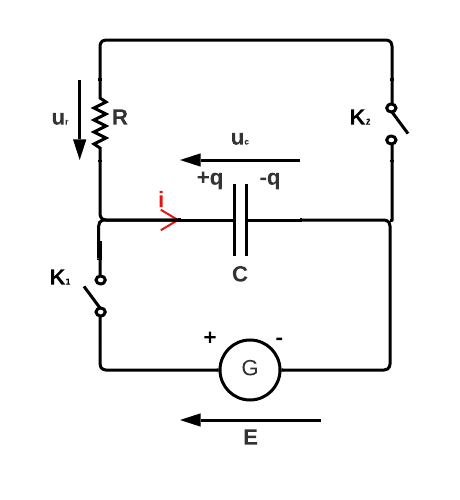
Figure 7. Circuit RC (décharge)
Remarque : A partir de maintenant, on ne fera plus la distinction entre \(i\) et \(i_c\), c'est-à-dire, que : \(i=i_c\).
Proposition 5. (Intensité aux bornes du condensateur en convention générateur)
Aux bornes d'un condensateur, l'intensité notée \(i_c\) s'exprime par la relation suivante :
Preuve
C'est la même preuve que dans la proposition 1.
4.2 Approche dynamique du circuit
L'objectif est de voir à quoi ressemble les expressions de \(u_c\) et \(i\). On procéde de la même façon, on cherche à établir une équation différentielle portée sur \(u_c\).
Proposition 6. (Expression de la tension \(u_c\))
La tension aux bornes du condensateur s'exprime par la relation :
où \(\tau=RC\) et \(u_c(0)=E\).
Preuve
On opère comme dans l'exercice précédent. On applique d'abord la loi des mailles dans le nouveau circuit étudié (maille du dessus) :
\[u_r(t)+u_c(t)=0\]
Ensuite, on utilise la loi d'Ohm couplée à la proposition 5 :
\[RC\frac{du_c(t)}{dt}+u_c(t)=0\]
On en déduit en posant \(\tau=RC\), l'équation différentielle suivante :
\[\frac{du_c(t)}{dt}+\frac{u_c(t)}{\tau}=0\]
D'après le cours, la forme générale des solutions de l'équation différentielle linéaire homogène d'ordre 1 est :
\[y(t)=C^{ste}exp\left(-\frac{t}{\tau}\right)\]
Comment déterminer \(C^{ste}\) ? Il nous faut une condition initiale. On suppose que le condensateur était totalement chargé à \(t=0\). Par continuité de la tension \(u_c\) au point 0 (basculement de l'interrupteur), on justifie l'égalité : \(u_c(t=0)=E\).
On en déduit que : \(C^{ste}=E\). Ce qui permet d'écrire finalement :
\[u_c(t)=Eexp\left(-\frac{t}{\tau}\right)\]
Ce qui achève la preuve.
Définition 8. (Le temps caractéristique du circuit RC série)
On peut définir une grandeur appelée temps caractéristique, notée généralement \(\tau=RC\), telle qu'à cet instant, \(u_c\) a diminué en atteignant 37\% de sa valeur initiale, \(E\) :
Remarque : Lorsqu'on procéde aux calculs, on peut montrer que : \(u_c(3\tau) \approx 0,05E\).
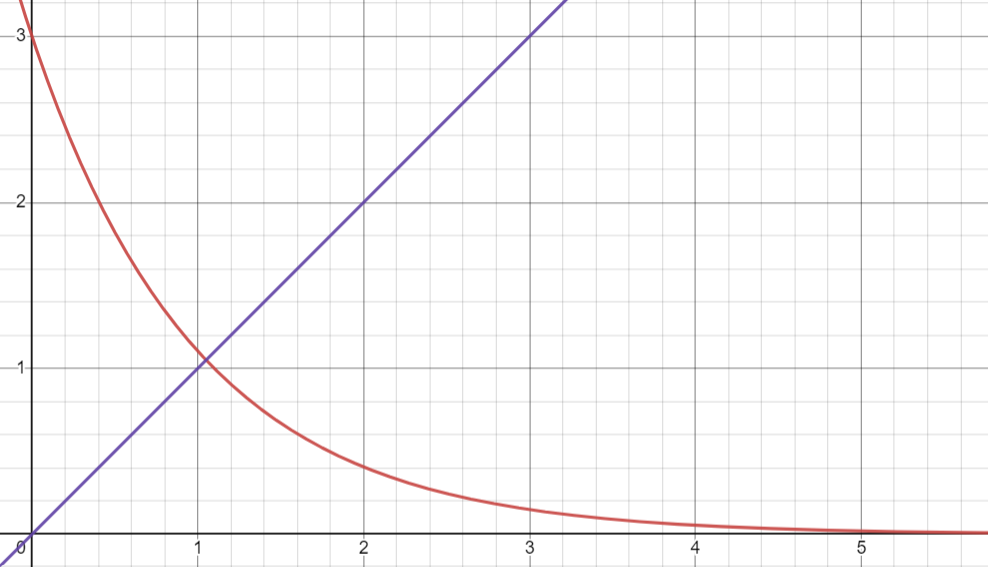
Figure 8. Tracé de \(u_c(t)\) (décharge)
Remarque : (lecture graphique). Ici, on peut encore graphiquement retrouver les valeurs de \(E\) et de \(\tau\). Lors de la décharge, à l'origine, \(u_c(0)=E\).
D'autre part, on sait qu'à \(t=\tau\), \(u_c(\tau) \approx 0,37E\). En cherchant l'abscisse correspondant à 37% de la valeur initiale, on trouve \(\tau\).
Proposition 7. (Expression de l'intensité \(i_c\))
L'intensité aux bornes du condensateur s'exprime par la relation :
où \(\tau=RC\).
Preuve
Il suffit d'utiliser la relation connue de \(i_c\) en fonction de \(u_c\) donnée par la proposition 5. On peut écrire : \[i_c(t)=C\frac{du_c(t)}{dt}=C\frac{d\left(Eexp\left(-\frac{t}{\tau}\right)\right)}{dt}=-\frac{EC}{\tau}exp\left(-\frac{t}{\tau}\right)=-\frac{E}{R}exp\left(-\frac{t}{\tau}\right)\] Ce qui achève la preuve.
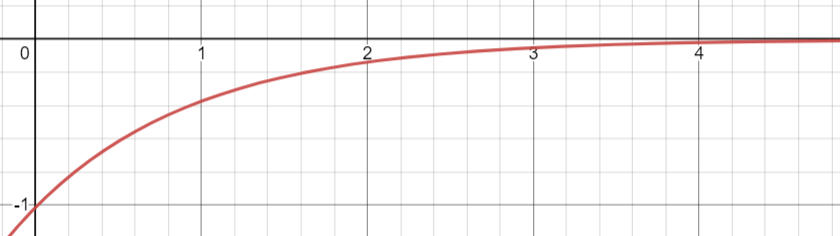
Figure 9. Tracé de \(i_c(t)\) (décharge)
Remarque : (Signe de \(i_c\)). Quelle est la différence entre \(i_c\) en convention récepteur (charge) et \(i_c\) en convention générateur (décharge) ?
Lorsque le condensateur se charge, sa tension \(u_c\) croît. Sa dérivée \(\frac{du_c(t)}{dt}\) est donc positive. Comme \(C>0\), il en résulte que : \(i_c(t)>0\).
Lorsque le condensateur se décharge, sa tension \(u_c\) décroît. Sa dérivée \(\frac{du_c(t)}{dt}\) est donc négative. Comme \(C>0\), il en résulte que : \(i_c(t)<0\).
Pour résumé, en convention récepteur, \(i_c(t)>0\) et en convention générateur (décharge, avec même sens de flèche pour i), \(i_c(t)<0\).