Terminale : Dynamique du point matériel
Étudier le mouvement d'un système, c'est faire de la cinématique. Néanmoins avant de débuter, il nous faut savoir quelles sont les causes qui ont provoqué son mouvement. C'est l'objet de ce cours qui s'intéresse à la dynamique de point matériel. Encore ici, on évoque l'hypothèse du point matériel qui a été traitée dans le cours sur la cinématique du point matériel et qui sera rediscutée en section 4.
📚 Table des matières
1. Notion abstraite de forces
1.1. Présentation du concept
Pour comprendre la mise en mouvement des objets, Isaac Newton a introduit le concept de forces. En quoi consiste ce concept ?
Newton a postulé que pour mettre en mouvement un objet, il fallait exercer sur lui une action. En d'autres termes, il faut « agir » sur l'objet. Cette action peut être faite par contact : balle tirée par le pied au foot ; cette action peut être faite à distance : l'action de la pesanteur que l'on ressent appelée aussi gravité. Ainsi, en connaissant toutes les forces qui s'exercent sur un objet, on pourrait grâce à des outils mathématiques les lier à la description du mouvement de l'objet : c'est l'intérêt du principe fondamental de la dynamique.
Newton choisit de modéliser graphiquement les forces à l'aide du concept de vecteurs en mathématiques : une force possède un point d'application, une direction, un sens et une norme. C'est le premier postulat (énoncé admis par la communauté scientifique) :
Postulat 1. (La force mécanique)
Toute force possède un point d'application parmi ceux qui constituent le système, une direction, un sens et une norme aussi appelée intensité de la force. Son unité est appelée le Newton (symbole : N).
Comme dit précédemment, il existe deux types de forces, celles qui agissent par contact et les autres par distance. C'est le second postulat.
Postulat 2. (Les types de forces)
Les forces se déclinent en deux sous-familles : les actions de contact et les actions à distance.
Exemple. Le poids et la force électrostatique sont des actions à distance. La force de rappel d'un ressort, la force de traction et les forces de frottements sont des actions de contact.
En mécanique, un système est soit soumis à aucune force soit à une ou plusieurs forces. En général, il est admis que le seul système soumis à aucune force est l'univers tout entier. Tous les autres systèmes possibles sont eux tous forcément soumis à au moins une force même si elle est d'intensité très faible. Il en suit la définition suivante :
Définition 1. (Les types particuliers de systèmes)
On dit d'un système qu'il est isolé lorsqu'il est soumis à aucune force. On dit d'un système qu'il est pseudo-isolé lorsque les forces qui s'exercent sur lui se compensent entre elles.
Remarque. Ainsi, l'univers est un système dit isolé. D'autre part, tout système isolé est un système pseudo-isolé si l'on considère des forces qui sont d'intensité nulle qui s'appliquent à notre système isolé.
Allons plus loin... dans la précision. Considérons un gaz de particules chargées. Choisissons comme système le gaz tout entier. Lorsqu'on réalise le bilan des forces qui s'exerce sur notre gaz, on ne recense que les forces dites « extérieures ». On est d'accord pour dire que dans le gaz, les particules s'exercent entre elles des actions à distance de nature électrique (forces électrostatiques). Mais ces dernières ne joueront aucun rôle dans la description du mouvement du système vu qu'elles restent internes au système et se compensent deux à deux (cf. section 4). C'est ce qui conduit à la méthode suivante :
Méthode. Bien entamer un problème de mécanique (ÉTAPE 1)
On définit le système à étudier puis on réalise le bilan des forces extérieures qui s'exercent sur notre système.
1.2. Exemples de forces
Nous avons vu dans la précédente section des exemples de forces mais nous n'avons pas vu leur forme vectorielle (leur écriture sous forme de vecteur comme le suggère le postulat 1).
La première force la plus évoquée est celle engendrée par la gravité. La force gravitationnelle n'est pas universelle, elle ne s'exerce pas de la même manière sur tout système. Tout corps génère autour de lui un champ de gravité tant qu'il est massif. Cela se résume dans le postulat qui suit :
Postulat 3. (Source de gravité)
Tout système de masse non nulle génère un champ de gravité tout autour de lui et qui agit dans toutes les directions de l'espace.
Le postulat 3 n'est pas vraiment un postulat mais il provient de l'écriture admise de la force gravitationnelle. Rappelons avant d'énoncer la définition qui suit, tout système \(\mathcal{S}\) dont on n'étudie pas les rotations peut être vu comme un point matériel écrit en son centre de gravité et de même masse (cf. cours sur la cinématique du point matériel où l'hypothèse a été évoquée).
Définition 2. (Expression de la force gravitationnelle)
Soient \(A\) et \(B\) deux points matériels, l'un de masse \(m\) et l'autre de masse \(M\). La force gravitationnelle qu'exerce le point \(A\) sur le point \(B\) prend la forme vectorielle suivante :
D'autre part, la force qu'exerce le point \(B\) sur le point \(A\) prend la forme vectorielle suivante :
Remarque : On peut observer qu'avec les notations de la définition précédente, on a : \[ \vec{F}_{A\rightarrow B}=-\vec{F}_{B\rightarrow A} \] c'est ce qu'on appelle la troisième loi de Newton : le principe des actions réciproques.
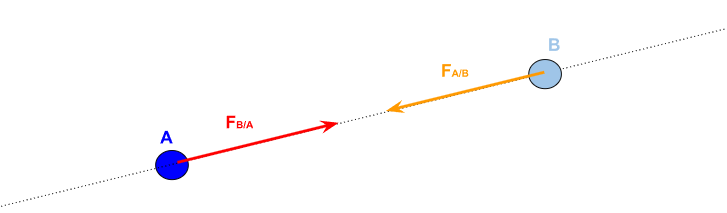
Figure 1. - Représentation vectorielle de la force gravitationnelle s'exerçant entre \(A\) et \(B\)
Remarque : La force gravitationnelle est une force attractive.
Pour affiner le postulat 3, nous allons définir le champ gravitationnel. Le champ gravitationnel est le champ vectoriel (champ constitué que de vecteurs) qui permet de ressentir, en un point, la présence d'une particule massive à proximité (la notion de proximité est subjective ici selon les échelles de distances mises en jeu).
Définition 3. (Expression du champ gravitationnel ou champ de gravité)
Soit \(A\) un point matériel de masse \(m\). Le champ gravitationnel ou champ de gravité qu'exerce le point \(A\) sur un point quelconque de l'espace \(B\) prend la forme vectorielle suivante :
Remarque : Avec les notations précédentes, si \(B\) est un point de masse \(M\), on peut écrire : \[ \boxed{\vec{F}_{A\rightarrow B}=M\times\vec{\mathcal{G}}_{A\rightarrow B}} \] Il est aussi commun de croiser la notation \(\vec{\mathcal{G}}_A(B)\) au lieu de \(\vec{\mathcal{G}}_{A\rightarrow B}\) en exercice. Ces deux notations bien que différentes représentent la même chose.
Définissons maintenant l'expression de la force électrostatique aussi appelée force électrique ou encore loi de Coulomb en hommage au scientifique qui a laissé son nom à l'unité de la charge électrique notée C (cf. cours sur l'électrocinétique). C'est la force qui s'exerce entre deux particules chargées. Par analogie à la force gravitationnelle, elle est engendrée par le champ électrique créé par chacune des particules chargées.
Postulat 4. (Source chargée)
Tout système de charge non nulle génère un champ électrique tout autour de lui et qui agit dans toutes les directions de l'espace.
Ce postulat à nouveau découle de la définition de la force électrique. Avant de l'écrire, précisons que comme pour le modèle du point matériel, il est possible de réduire tout système chargé à une particule de même charge. La particule sera réduit au point qui constitue le centre des charges électriques (à la différence du cas gravitationnel où c'était le centre de masse).
Définition 4. (Expression de la force électrique)
Soient \(A\) et \(B\) deux particules chargées, l'une de charge \(q\) et l'autre de charge \(Q\). La force électrique qu'exerce le point \(A\) sur le point \(B\) prend la forme vectorielle suivante :
D'autre part, la force qu'exerce le point \(B\) sur le point \(A\) prend la forme vectorielle suivante :
Remarque : On peut à nouveau observer qu'avec les notations de la définition précédente, on a : \[ \vec{F}_{A\rightarrow B}=-\vec{F}_{B\rightarrow A} \]
Remarque : La force électrique est une force attractive si les charges électriques sont de signe opposé et répulsive lorsqu'elles ont le même signe.
De la même manière que pour le champ gravitationnel, nous allons définir aussi l'expression du champ électrique. C'est le champ vectoriel qui permet de ressentir, en un point, s'il existe à proximité une particule chargée.
Définition 5. (Expression du champ électrique ou champ électrostatique)
Soit \(A\) un point chargé de charge \(q\). Le champ électrique ou champ électrostatique qu'exerce le point \(A\) sur un point quelconque de l'espace \(B\) prend la forme vectorielle suivante :
Remarque : Avec les notations précédentes, si \(B\) est un point de charge \(Q\), on peut écrire : \[ \boxed{\vec{F}_{A\rightarrow B}=Q\times\vec{\mathcal{E}}_{A\rightarrow B}} \] Il est aussi commun de croiser les notations \(\vec{\mathcal{E}}_A(B)\) ou \(\vec{E}_A(B)\) au lieu de \(\vec{\mathcal{E}}_{A\rightarrow B}\) en exercice. Ces trois notations bien que différentes représentent la même chose.
Il existe d'autres forces comme la force de rappel d'un ressort qui vérifie dans un certain domaine, ce qu'on appelle la loi de Hooke (HP) qui est un modèle de force élastique ; la tension ressentie par un fil qui n'a pas d'expression propre ; la réaction normale subie par le support qui s'oppose à une partie du poids (plus précisément son projeté suivant la normal au support) ou encore les forces de frottements dont il existe pleins de modèles différents pour les décrire.
Intéressons nous maintenant à la définition du poids sur Terre. Dans une certaine mesure, le poids n'est pas vraiment défini comme il le sera dans la suite (du fait que le référentiel terrestre n'est pas galiléen par rapport au référentiel géocentrique) mais pour le montrer cela dépasse largement le cadre du programme. Proposons alors un modèle simplifié de poids terrestre.
La force gravitationnelle qu'exerce la Terre (réduit à son centre de masse noté \(O_T\) de masse \(M_T\)) sur un objet quelconque à sa surface (réduit à un point \(O\) de masse \(m\)) à une altitude \(h\) faible, c'est-à-dire \(h \ll R_T\) où \(R_T\) est le rayon terrestre, peut s'écrire : \[ \vec{F}_{O_T\rightarrow O}=-G\frac{mM_T}{R_T^3}\overrightarrow{O_TO} \] On note par la suite \(\vec{\mathcal{G}_T(O)}\) le champ de gravité généré par la Terre en \(O\) : \[ \vec{\mathcal{G}}_T(O)=-G\frac{M_T}{R_T^3}\overrightarrow{O_TO} \] On montre alors qu'en norme, pour \(h=0\), \(||\vec{\mathcal{G}}_T(O)||\approx\) 9,81 m.s⁻¹. On pose par convention \(g\) l'intensité de pesanteur comme étant égale à la norme du champ gravitationnel à la surface terrestre et \(\vec{g}\) son vecteur associé : \[ g=||\vec{\mathcal{G}}_T(h=0)||\quad \textrm{et} \quad \vec{g}=\vec{\mathcal{G}}_T(h=0) \] Ainsi, on peut définir le poids définit comme étant le vecteur \(\vec{P}\) et qui s'écrit : \[ \boxed{\vec{P}=m\vec{g}} \] On retrouve bel et bien la définition du poids qui s'exprime en Newton.
1.3. Limite du concept de forces (HP)
Pour finir cette section, parlons des limites liées à ce concept. C'est en particulier, ce qui a animé Einstein a allé voir d'autres horizons pour élaborer une nouvelle théorie plus sophistiqué qui tient compte des effets physiques que l'on observe dans la vie : dilatation du temps (le temps n'est pas uniforme, il ne s'écoule pas de la même façon là où on se trouve dans l'univers), contraction des longueurs (les objets se contractent sur eux-mêmes quand leur vitesse approche celle de la lumière définie comme une limite des vitesses dans le vide), la déformation des surfaces... on parle alors d'effets relativistes de l'espace-temps.
Comment fait un objet \(A\) pour savoir qu'un objet \(B\) est à proximité de lui pour savoir s'il doit agir sous l'effet d'une force ou non ? Réalisons une expérience de pensée en considérant la Lune et la Terre. C'est grâce à l'attraction gravitationnelle que la Lune orbite autour de la Terre, c'est pour cela qu'on parle aussi de satellite naturel. Mais par quel phénomène, la Lune sait qu'elle doit orbiter autour de la Terre ? La Terre communique-t-elle avec la Lune par un transfert de flux d'informations ? Si l'on pense qu'il existe un tel transfert d'informations donc des particules « spéciales » qui apporte à la Lune l'information que la Terre se trouve à proximité d'elle, cela conduit à une absurdité... En effet, cela laisse envisager que ces particules se propagent à une vitesse qui est « infinie », donc bien plus grande que celle de la lumière, c'est impossible !
Donc on ne voit pas comment unifier ce concept à la réalité de ce que l'on perçoit. Il faut alors abandonner ce concept... en fait, pas vraiment. On pourra toujours parler de forces pour parler d'actions, c'est une transcription de la réalité que l'on observe. Ce concept n'est pas réel mais décrit simplement les actions mécaniques, on peut alors le garder. Pour le garder, il faut ajouter les deux postulats suivants :
Postulat 5. (Forces et référentiels)
L'écriture des forces est indépendante du référentiel choisi.
Postulat 6. (Vitesse de la lumière)
La vitesse de la lumière est la même dans tous les référentiels. La lumière impose comme étant une limite physique des vitesses, sa vitesse dans le vide. On la note \(c\) et elle vaut environ \(3.10^8\) m.s⁻¹.
Remarque : Pour une étude plus approfondie sur le sujet, on oriente le lecteur averti vers les cours de relativité (d'abord restreinte puis générale) pour mieux saisir la limite fixée par le modèle newtonien.
2. Les lois de Newton
2.1. Principe d'inertie
Ici, on introduit la première loi de Newton, vu comme son premier postulat, qui permet d'étudier les systèmes à vitesse constante ou inversement, les systèmes pseudo-isolés.
Principe 1. (Principe d'inertie - 1ère loi de Newton)
Il existe une classe de référentiels privilégiées dans lesquels tout système pseudo-isolé est soit immobile soit en mouvement rectiligne uniforme. Ces référentiels sont appelés référentiels galiléens.
Remarque : Le référentiel héliocentrique peut être supposé galiléen en toute circonstance. Pour une analyse plus approfondie, le référentiel héliocentrique appelé aussi référentiel de Kepler est en translation par rapport au référentiel de Copernic (lié au centre de masse du système solaire, très proche du centre de masse de Terre) et le référentiel de Copernic est presque proche d'être galiléen.
Le référentiel géocentrique peut être supposé galiléen pour des expériences étudiées sur une échelle de temps très faible devant un an. C'est en particulier le cas pour l'étude du mouvement de la Lune autour de la Terre ou encore de l'ISS autour de la Terre.
Enfin, le référentiel terrestre peut être supposé galiléen pour des expériences étudiées sur une échelle de temps très faible devant un jour. C'est en particulier le vrai lorsqu'on étudie un lancer d'objet par exemple.
Remarquons que le caractère galiléen est étroitement lié à la durée du phénomène. Il suffit de s'en convaincre en se disant que les phénomènes à l'origine du caractère non galiléen des référentiels étudiés (initialement avant toute hypothèse) n'ont pas le temps d'«assez agir» en peu de temps devant les temps de révolution de ces référentiels.
Nous ne développerons pas pourquoi ces référentiels ne sont pas au départ galiléens mais il peut être intéressant de retenir que c'est l'effet des marées qui permet de mettre en évidence que le référentiel géocentrique n'est pas galiléen et que c'est la légère déviation vers l'est des objets en chute libre qui met en évidence le caractère non galiléen du référentiel terrestre.
Remarque : On peut aussi récrire la première loi de Newton comme suit : \[ \boxed{\vec{v}=\overrightarrow{C^{ste}}\iff\sum_{i}\vec{F}_i^{(ext)}=\overrightarrow{0}} \] où \(\vec{v}\) désigne la vitesse de notre système et \(\vec{F}_i^{(ext)}\) une des forces extérieures subie par le système.
Définition 6. (Référentiel galiléen - Première version)
Un référentiel est galiléen lorsqu'il vérifie le principe d'inertie.
On peut aussi établir l'équivalence (HP) suivante entre la définition précédente et celle qui suit :
Définition 7. (Référentiel galiléen - Seconde version (HP))
Un référentiel est galiléen lorsqu'il est constitué d'un espace homogène et isotrope et d'un temps uniforme.
(HP+) Précisons les termes employés dans cette définition. Un espace est homogène lorsque si l'on effectue une translation d'une unité d'espace alors on obtient le même espace. Un espace est isotrope lorsque les lois de la physique sont les mêmes suivant n'importe quelle direction choisie. Le temps est uniforme dans un référentiel lorsque les lois de la physique dans ce référentiel ne dépendent pas de l'instant considéré pour les écrire.
Cette écriture permet d'écrire le principe de relativité de Galilée qui suit :
Principe 2. (Principe de relativité de Galilée)
Les lois de la physique sont les mêmes dans tous les référentiels galiléens.
Remarque : Cette écriture rappelle le postulat 6 avec la vitesse de la lumière. On fixe là encore, une harmonisation pour accorder ce que l'on obtient par le calcul avec ce que l'on observe en pratique.
2.2. Principe fondamental de la dynamique
Ici, on énonce un nouveau principe, le principe fondamental de la dynamique appelé aussi seconde loi de Newton. Il permet, comme dit dans le paragraphe § 1.1, de concilier le modèle mathématique de forces aux outils de la cinématique. Il s'énonce comme tel :
Principe 3. (Principe fondamentale de la dynamique - 2ème loi de Newton)
Soit \(\vec{p}\) la quantité de mouvement d'un système \(\mathcal{S}\) de masse \(m\) et de vitesse \(\vec{v}\) qui subit un ensemble de forces extérieures \(\vec{F}_1,\vec{F}_2,...,\vec{F}_i\) alors il possible d'écrire l'égalité suivante dans tout référentiel galiléen :
Remarque : Cette écriture n'est encore valable que parce qu'il est possible de réduire à un point matériel de même masse notre système (cf. section 4 pour plus d'informations) car on ne s'intéresse pas à ses mouvements de rotation. Toujours dans l'hypothèse du point matériel, l'égalité précédente s'écrit pour le point matériel qui coïncide avec le centre de gravité du système \(\mathcal{S}\). Ainsi, il est plus présentable de parler de quantité de mouvement lié au centre de gravité noté \(G\), d'impulsion \(\vec{p}_G\).
Après cette remarque précieuse, le principe fondamental de la dynamique se réécrit : \[ \boxed{\frac{d\vec{p}_G}{dt}=\sum_{i=1}^n\vec{F}_i} \] et en notant \(\vec{v}_G\) la vitesse de \(G\) et on suppose la masse \(m\) constante, \[ \boxed{m\frac{d\vec{v}_G}{dt}=\sum_{i=1}^n\vec{F}_i} \] qui est aussi équivalente à la forme suivante si l'on note \(\vec{a}_G\) l'accélération de \(G\) : \[ \boxed{m\vec{a}_G=\sum_{i=1}^n\vec{F}_i} \] c'est cette dernière forme qu'on retient en général.
On observe qu'il est possible de retomber sur le principe d'inertie lorsqu'on fait l'hypothèse d'un système pseudo-isolé. Il sera alors soit immobile soit en mouvement rectiligne uniforme.
2.3. Principe des actions réciproques
Ici, on développe la troisième loi de Newton aussi appelée principe des actions principes. En bref, si un corps \(A\) exerce une force sur \(B\) alors \(B\) exerce sur \(A\) l'opposé de cette force. On résume cela dans l'énoncé suivant :
Principe 4. (Principe des actions réciproques - 3ème loi de Newton)
Tout système qui exerce une force sur un autre système système ressent de ce dernier la même force.
Remarque : Si l'on note \(A\) et \(B\) nos deux systèmes et qu'on note \(\vec{F}_{A\rightarrow B}\) la force qu'exerce \(A\) sur \(B\) ou encore la force que subit \(B\) par \(A\) alors : \[ \boxed{\vec{F}_{A\rightarrow B}=-\vec{F}_{B\rightarrow A}} \] On retrouve les remarques faites aux définitions 2 et 4.
3. Conservation de la quantité de mouvement
Ici, nous développons un principe qui a déjà été utilisé dans le cours sur la cinématique du point matériel pour étudier la vitesse de décollage d'une fusée. D'abord, définissons les mots qu'on utilisera par la suite pour énoncer les hypothèses de validité du principe de conservation de la quantité de mouvement :
Définition 8. (Système fermé et système ouvert au sens thermodynamique)
On dit d'un système qu'il est fermé lorsqu'il conserve sa masse au cours du temps. On dit d'un système qu'il est ouvert lorsqu'il échange de la masse avec l'extérieur.
Remarque : Dans les deux cas, fermé ou isolé, rien n'exclut que le système échange ou pas de l'énergie avec l'extérieur. On ajoutera la précision isolé au système s'il n'échange ni masse ni énergie avec l'extérieur en thermodynamique et simplement fermé s'il n'échange pas de masse avec l'extérieur mais s'autorise à échanger avec l'extérieur de l'énergie.
En définissant la notion de système fermé au sens thermodynamique, il est possible d'énoncer le principe de conservation de la quantité de mouvement.
Principe 5. (Principe de conservation de la quantité de mouvement)
Dans un référentiel galiléen, tout système isolé au sens mécanique et fermé au sens thermodynamique voit sa quantité de mouvement se conserver au cours du temps.
Remarque : En général, un système isolé au sens mécanique (au sens de la définition 1) est toujours fermé au sens thermodynamique (au sens de la définition 8). Il suffit alors de définir un système isolé au départ et d'appliquer le principe dans un référentiel dans un référentiel galiléen.
On applique le principe de conservation de la quantité de mouvement lorsqu'on étudie une collision entre deux objets qui forment un système isolé, une fusée qui éjecte au cours du temps du carburant sous forme de gaz en considérant le système isolé {fusée-carburant-gaz}. Le second exemple a été traité dans le cours de cinématique du point matériel.
Méthode. Poursuivre un problème de mécanique (ÉTAPE 2)
Après avoir fait l'étape 1, on définit le référentiel d'étude dans lequel on se place. On choisit le référentiel le plus approprié au problème étudié. Ensuite, on applique les différents principes en veillant à vérifier que les hypothèses sont bien les bonnes (isolé pour le principe 5, de masse constante pour la forme explicite du principe 3...).
4. Le modèle du point matériel - (HP)
Dans cette section hors programme, nous allons détailler la validité du modèle du point matériel : lorsqu'on étudie que le mouvement de translation d'un solide alors il est possible de ramener son étude à son centre de gravité en y concentrant toute sa masse en ce point puis on verra que le principe fondamental de la dynamique est valide dans ce cas précisément.
Considérant un système discret de masse fini \(m\) (constitué de points en nombre fini) à \(N\) points notés \(M_1,M_2,...,M_N\). Soit \(M_k\) un point quelconque du système et on note \(\vec{V}_{M_k}\) sa vitesse. En notant \(G\) le barycentre (centre de gravité) de ce système et \(\vec{V}_{G}\) sa vitesse alors on peut écrire : \[ \overrightarrow{V_{M_k}}=\overrightarrow{V_{G}}+\overrightarrow{\Omega}_{M_k/G}\wedge\overrightarrow{GM_k} \] Comme on suppose qu'on étudie qu'une simple translation alors les termes de rotation sont nuls, c'est-à-dire : \[ \overrightarrow{\Omega}_{M_k/G}=0 \] donc il en suit, que pour tout \(k\), \[ \overrightarrow{V_{M_k}}=\overrightarrow{V_{G}} \] Il est alors valide de dire que le système a la même translation que celui de son centre de masse. Maintenant, montrons que \(G\) est le seul point qui permet de garder en place l'égalité apporté par la seconde loi de Newton. Supposons qu'on est dans un référentiel galiléen et on suppose que le système subit de l'extérieur une force résultante (la somme de ces forces extérieures) notée \(\vec{R}^{(ext)}\) et on prend en compte les forces internes qu'exercent \(M_i\) sur \(M_j\). De manière non simplifiée, on a : \[ m\frac{d\vec{V}_G}{dt}=\vec{R}^{(ext)}+\sum_{j=1}^N\sum_{i=1,i\ne j}^N\vec{F_i}_{M_i\rightarrow M_j} \] D'après la troisième loi de Newton, le second terme constitué de la double somme est nul car les forces de la forme \(\vec{F_i}_{M_i\rightarrow M_j}\) et \(\vec{F_i}_{M_j\rightarrow M_i}\) s'annulent donc on a bien : \[ \sum_{j=1}^N\sum_{i=1,i\ne j}^N\vec{F_i}_{M_i\rightarrow M_j}=0 \] et il en suit que la seconde loi de Newton, comme postulées dans § 1.1, ne prend bien pas en compte les forces internes au système : \[ m\frac{d\vec{V}_G}{dt}=\vec{R}^{(ext)} \] Concluons sur le fait que ce modèle, si l'on veut étudier aussi les rotations du système sur lui-même, il nous faudra alors considérer un volume complet non nul ce qui s'opposera à l'hypothèse du point matériel car un point est de volume nul. Ainsi, jamais l'hypothèse du point matériel ne pourra conclure sur la description mécanique des rotations d'un système (pour aller plus loin, consulter le cours sur les moments d'une force, chapitre vu en première année de CPGE scientifique).