Terminale : Effet Doppler
Ce chapitre s'intéresse en particulier à l'effet Doppler, un phénomène physique rencontré chaque jour qui traduit comment les ondes se déforment en s'écartant ou en se rapprochant pour rendre un son plus aigu, plus grave ou même une couleur plus vive ou plus foncée.
C'est un chapitre sans trop de difficulté, la première section permet d'apporter quelques définitions autour des ondes qui seront utilisées dans la section 2 et en particulier dans le paragraphe § 2.2. lors de la traduction mathématique du phénomène étudié. La section 3, facultative, permet de voir quelques exemples dans la vie de l'utilisation de l'effet Doppler. De plus, la section 3 met en avant l'approche géométrique des problèmes étudiés lorsqu'on parle de nombre de Mach qui introduit la notion de cône de Mach ou encore pour comprendre ce qu'est l'effet Tcherenkov en analogie à l'étude du son. Enfin, la section 4 présente la notion d'intensité sonore présente dans le programme et qui permet de définir des seuils de danger pour l'audition.
📚 Table des matières
1. Les ondes périodiques - une brève introduction
Définition 1. (Onde)
Une onde désigne la propagation d'un phénomène de perturbation dans un milieu matériel ou non qui déforme de façon réversible ses propriétés.
Remarque : La lumière est une onde qui se propage dans tout milieu matériel mais aussi dans le vide. Le son est une onde qui se propage que dans les milieux matériels mais ne se propage pas dans le vide.
Au lycée, on s'intéresse aux ondes mécaniques comme le son (c'est le cas de ce chapitre) et à la lumière lorsqu'on étudie le phénomène de diffraction avec l'expérience des trous d'Young. Intéressons nous aux ondes mécaniques.
Définition 2. (Onde mécanique)
Une onde mécanique est une onde qui se propage dans un milieu matériel.
Définition 3. (Onde mécanique progressive)
Une onde mécanique progressive est une onde qui se propage dans un milieu matériel transportant de l'énergie sans transport global de matière.
Remarque : Ici, on précise bien qu'une onde mécanique progressive ne transporte pas de matière globalement mais localement, cette dernière peut transporter de la matière. Il suffit de penser aux vagues, qui sont des ondes, transportant localement de l'eau. En revanche, globalement, les vagues ne déplacent pas d'eau.
On définit maintenant les grandeurs liées à une onde mécanique progressive. Plus généralement, les prochaines définitions seront définies pour des ondes progressives qui ne sont que des ondes qui se propage dans un milieu matériel ou non en transportant seulement de l'énergie.
Définition 4. (La célérité)
La célérité est la vitesse de propagation d'une onde progressive. Elle s'exprime en m.s⁻¹.
Remarque : Elle est à connaître : la célérité de la lumière dans le vide notée \(c\) vaut environ \(3 \times 10^8\) m.s⁻¹.
Définition 5. (Onde périodique)
Une onde est périodique lorsqu'elle est constituée d'un motif qui se répètent dans le temps de manière identique.
Remarque : La lumière est, par exemple, une onde progressive périodique.
Définition 6. (Le motif élémentaire)
On appelle motif élémentaire d'une onde période, le plus petit motif qui se répètent de façon identique dans le temps.
Définition 7. (La période temporelle)
On définit la période temporelle notée \(T\) comme étant la durée du motif élémentaire d'une onde périodique.
Définition 8. (La fréquence)
On définit la fréquence notée \(f\) comme le nombre de fois où le motif élémentaire d'une onde périodique se répètent par unité de temps. Elle s'exprime en Hz.
Remarque : Pour une onde sonore, la gamme des fréquences audibles pour l'oreille humaine est : \[ [20 \text{ Hz}, 20 \text{ kHz}] \]
Propriété 1. (Période temporelle - Fréquence)
Soit une onde périodique de période temporelle \(T\) et de fréquence \(f\). La période temporelle et la fréquence sont liées par la relation suivante :
Remarque : En exercice, il est très fréquent d'avoir des signaux représentés graphiquement et on peut être amené à calculer leur fréquence \(f\). Pour cela, il suffit de mesurer la durée du motif élémentaire, c'est-à-dire leur période temporelle notée \(T\) puis d'utiliser la relation donnée par la proposition 1 : \[ \boxed{f=\frac{1}{T}} \]
On définit une autre période, celle-ci d'origine spatiale. En effet, une onde lorsqu'elle se propage, peut être observer selon deux points de vue différents : une observation spatiale de l'onde où on voit comment elle se propage suivant son axe de propagation en un point de cet axe qu'on s'imagine être ; une observation temporelle où on observe comment l'onde se propage dans le temps.
Remarque : Les représentations temporelle et spatiale d'une onde mécanique progressive sont symétriques : une augmentation puis une diminution en temporelle correspond à une diminution puis à une augmentation en spatial.
Ainsi, on a vu qu'il existait une période dans le temps mais il existe aussi une période spatiale pour tout onde périodique. Cette dernière correspond à la longueur du motif élémentaire et non pas à sa durée comme l'est la période temporelle. On parle alors de période spatiale ou encore de longueur d'onde.
Définition 9. (La période spatiale - la longueur d'onde)
On définit la période spatiale, appelée aussi longueur d'onde, notée \(\lambda\) comme la longueur du motif élémentaire d'une onde périodique.
Propriété 2. (Période spatiale - Fréquence)
Soit une onde période de période spatiale \(\lambda\) et de fréquence \(f\). La période spatiale et la fréquence sont liées par la relation suivante :
Remarque : Cette relation est analogue à celle obtenue à la proposition 1. Ces relations peuvent se retrouver dans le cas particulier où l'onde considérée est une sinusoïde. Il suffit de voir qu'une onde sinusoïdale est périodique à la fois dans l'espace et dans le temps. En utilisant cette double périodicité, on arrive à retrouver les deux égalités. La démonstration de ces deux résultats reste quant à elle hors programme.
Il en résulte qu'on peut trouver la relation qui lie la période temporelle à la période spatiale en regroupant ces deux égalités. Cette égalité est souvent plus connue et permet de calculer la longueur d'onde lorsqu'on mesure seulement la durée du motif élémentaire d'une onde périodique.
Propriété 3. (Période temporelle - Période spatiale)
Soit une onde période de période temporelle \(T\) et de période spatiale \(\lambda\). La période temporelle et la période spatiale sont liées par la relation suivante :
Remarque : Comme la lumière est une onde périodique elle aussi alors, on peut écrire la relation aussi connue : \[ \lambda=T\times c \] avec \(\lambda\) sa longueur d'onde (pour la lumière, cela peut correspondre aussi à la couleur d'un rayon lumineux), \(T\) sa période dans le temps et \(c\) sa célérité dans le vide. Il en suit qu'en manipulant les résultats précédents, connaissant par exemple la fréquence d'un laser, on peut retrouver la longueur d'onde du rayon lumineux émis.
Avec toutes ces définitions et ces résultats, on peut introduire correctement l'effet Doppler.
2. L'effet Doppler
2.1. Présentation du phénomène physique
Lorsqu'une ambulance s'approche de nous, le son de sa sirène est de plus en plus aigu. Lorsqu'elle s'éloigne, ce son devient grave. C'est ce qu'on appelle l'effet Doppler.
On assimile la sirène à un émetteur d'ondes, il émet des ondes qui sont des ondes mécaniques progressives (l'ensemble des ces ondes forme le son de la sirène). Ces ondes se déplacent à une vitesse \(u\) dans toutes les directions de l'espace mais l'émetteur accroché à l'ambulance se déplacent de façon rectiligne à une vitesse \(v\).
Ainsi, on peut s'imaginer que si l'on considère les ondes qui se propagent dans le même sens que l'émetteur, alors les ondes vont être de plus en plus proches, la longueur du motif élémentaire du son sera plus petite (distance entre deux ondes successives dans ce cas) et donc la période temporelle plus petite d'après la propriété 3 à vitesse constante. Finalement, la relation de la proposition 1 (ou 2) permet de conclure que la fréquence sera plus élevée. Le son perçu est alors plus aigu.
Résumons ça à l'aide d'une figure :
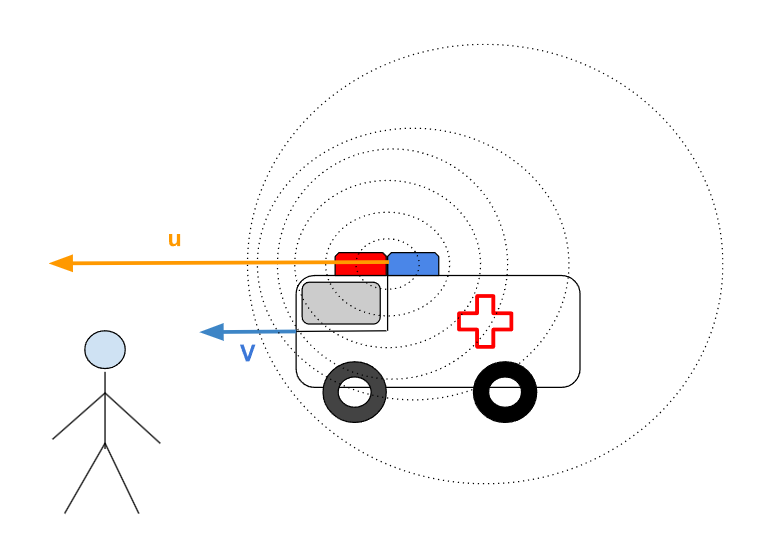
Figure 1. - Mise en évidence de l'effet Doppler pour une ambulance en mouvement
La figure 1 nous permet de visualiser, si nous étions l'observateur fixe et qu'on pouvait voir les ondes sonores, qu'à l'avant de l'ambulance les ondes s'écrasent de plus en plus rétrécissant ainsi la longueur d'onde du son perçu. C'est ainsi que la fréquence du son perçu est plus élevée et donc le son plus aigu.
2.2. Origine physique du phénomène - résolution mathématique
Dans ce paragraphe, on va trouver le lien entre la fréquence constante des ondes émises par l'émetteur qu'on notera \(f_e\) et la fréquence du son perçu par l'observateur immobile dans le référentiel terrestre qu'on notera \(f_r\). Rappelons que \(v\) désigne la vitesse de l'émetteur et \(u\) correspond à la célérité des ondes émises par l'émetteur. Finalement, on nommera \(T_e\) la période temporelle de l'émetteur et \(T_r\) la période temporelle du son perçu.
L'objectif de la démonstration est d'étudier quatre instants distincts, le premier correspondant à l'émission de la première onde mécanique par l'émetteur, le second correspondant à l'instant au bout duquel l'observateur perçoit l'onde, le troisième correspondant à l'instant où l'émetteur émet une seconde onde et enfin le dernier correspondant à l'instant au bout duquel l'observateur perçoit cette seconde onde. Voici une figure de la situation considérée lorsque l'émetteur se rapproche de l'observateur :
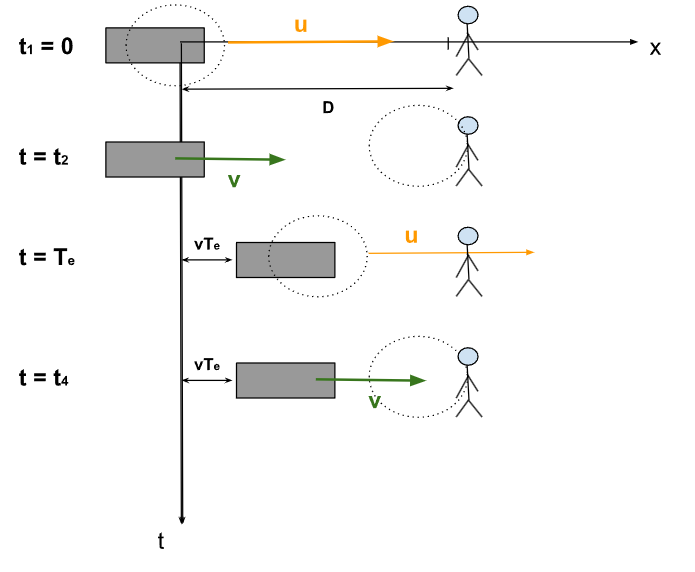
Figure 2. - Mise en situation du problème étudié
Dans la suite \(D\) désigne la distance initiale entre l'émetteur et l'observateur, c'est-à-dire à \(t=0\).
Déterminons les expressions de \(t_1\), \(t_2\), \(t_3\) et \(t_4\). D'abord \(t_1=0\) car c'est notre origine pour le temps (instant correspondant à l'émission d'une première onde). Il est facile d'exprimer \(t_2\) par la relation : \[ t_2=\frac{D}{u} \] Par ailleurs, il est imposé que \(t_3=T_e\) car c'est l'instant qui correspond à l'émission de la seconde onde qui se fait après une durée égale à la période temporelle de l'émetteur. Enfin, on observe que \(t_4\) s'exprime comme : \[ t_4=\frac{D-vT_e}{u}+T_e \] L'observateur reçoit en \(t=t_2\) et en \(t=t_4\) deux ondes successives, ainsi, le calcul de la période temporelle liée au son perçu par l'observateur qu'on a noté \(T_r\) est donnée par la durée entre deux ondes successives : \[ T_r=t_4-t_2 \] Finalement, en développant, on peut écrire : \[ T_r=\frac{D-vT_e}{u}+T_e-\frac{D}{u} \] d'où : \[ T_r=\left(1-\frac{v}{u}\right)T_e \] En utilisant la relation de la proposition 1, on en déduit :
Si \(u>v\) alors la fréquence perçue est plus élevée que la fréquence émise donc le son entendue est plus aigu. Si \(v=0\), l'émetteur est alors immobile et les fréquences sont égales. C'est bien cohérent avec ce qu'il pourrait être observé dans la vraie vie. Quand \(v>u\), la fréquence est négative, ce qui n'a pas de sens physique étant donné que la fréquence est positive. De même si \(u=v\), on divise la fréquence émise par 0 ce qui n'a pas de sens physique aussi. Ces deux cas sont des limites à notre modèle, ils seront discutés à la section 3 en introduisant la notion de nombre de Mach et de cône de Mach dans le cas d'ondes sonores.
En introduisant la vitesse réduite notée \(\beta\) telle que : \[ \beta=\frac{v}{u} \] alors \(\beta<1\) pour correspondre au domaine de validité du modèle et la relation (1) devient :
Remarquons que dans le cas où l'émetteur s'éloigne de l'observateur, la fréquence perçue est plus petite que la fréquence émise, le son entendu est alors plus grave et ce peu importe la valeur de la vitesse \(v\) par rapport à la vitesse \(u\). Le paragraphe § 3.1. introduira deux nouvelles formules pour décrire l'effet Doppler lorsqu'un observateur est en mouvement et non plus immobile.
2.3. Quelques applications
2.3.1. Le radar fixe
La radar fixe est un appareil de mesure des vitesses qui a son fonctionnement basée sur l'effet Doppler. Modélisons la mesure par un radar en situation réelle avec la figure suivante :
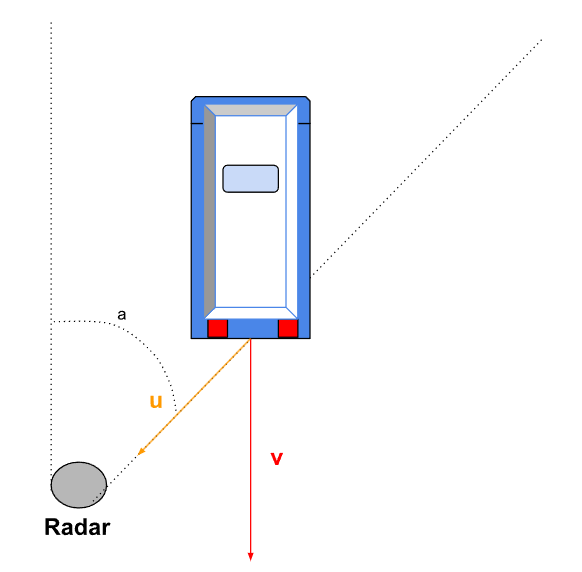
Figure 3. - Mise en situation du problème étudié
On considère un véhicule qui roule à la vitesse \(v\) suivant la verticale. Le radar a un champ d'action oblique, décalé vers la droite d'un angle \(a\) avec la verticale. Pour le radar, la vitesse de l'émetteur est égale à \(u\), c'est-à-dire la projection de la vitesse \(v\) sur l'axe de mesure du radar.
Le radar fonctionne comme suit : il émet une série d'ondes électromagnétiques de fréquence \(f_e\) et qui ont une célérité, qu'on suppose, égale à celle de la lumière dans le vide, notée \(c\). Lorsqu'un véhicule entre dans le champ d'action du radar, une des ondes électromagnétique émise se réfléchit sur la carrosserie du véhicule (c'est une réflexion quasi-totale car la carrosserie est en métal) et acquiert une nouvelle fréquence liée à la vitesse du véhicule. Cette fréquence correspond à la fréquence de l'onde électromagnétique perçue par le véhicule qu'on note \(f_r\).
Cette onde se réfléchit vers le radar qui mesure sa fréquence ensuite il réalise la différence des fréquences entre la fréquence perçue et la fréquence émise notée \(\delta f=f_r-f_e\). Comme le véhicule se rapproche du radar et le radar est immobile, on utilise la formule (1) : \[ \boxed{f_r=\frac{c}{c-u}f_e} \] D'après les formules trigonométriques, on exprime facilement \(u\) : \[ u=v\cos(a) \] On en déduit alors que : \[ f_r=\frac{c}{c-v\cos(a)}f_e \] ce qui conduit à établir le résultat suivant : \[ v=\frac{\delta f}{\cos(a)f_e}c \] Attention, le résultat n'est pas vraiment bon. En effet, ici, l'onde réalise un aller-retour entre le radar et la voiture, comme le temps de parcours par à un simple trajet est deux fois plus élevé alors la différence de fréquence associée est deux fois plus petite donc la vitesse est deux fois plus faible. C'est ce qui permet de justifier l'origine d'un facteur \(\frac{1}{2}\) dans la vraie formule : \[ \boxed{v=\frac{\delta f}{2\cos(a)f_e}c} \]
2.3.2. L'échographie Doppler
Une échographie Doppler est un exemple d'application de l'effet Doppler en médecine. Intéressons nous au cas où l'on cherche à mesurer la vitesse des globules rouges.
On considère une sonde qui émet et reçoit des ondes sonores qui ne sont pas audibles pour l'oreille humaine, de fréquence en dehors de la gamme audible (ce sont des ultrasons). On note \(f_e\) la fréquence des ondes sonores émises et \(f_r\) la fréquence des ondes sonores reçues. On modélise la mesure du flux sanguin dans un vaisseau sanguin :
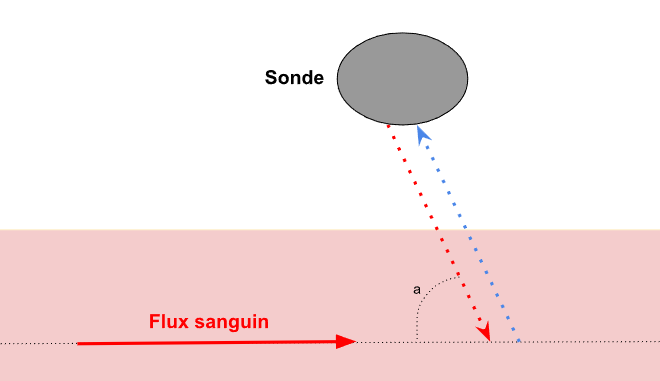
Figure 4. - Mise en situation du problème étudié
La flèche en pointillé rouge indique le sens d'émission des ondes sonores et la flèche en pointillé bleue indique le sens de réception des ondes sonores. On note \(v\) la vitesse des globules rouges et \(u\) sa projection dans la direction de la sonde. Le mode de démonstration est similaire au radar. Notons \(w\) la célérité des ondes sonores émises par la sonde.
La sonde a le même mode de fonctionnement que le radar donc en reprenant la même démonstration que dans le paragraphe 2.3.1. en ajustant les notations, on a : \[ \boxed{v=\frac{\delta f}{2\cos(a)f_e}w} \] On notera qu'ici, le rôle de la voiture est joué par un globule rouge pris au hasard dont on calcule la vitesse. C'est à l'aide cette relation que la sonde mesure la vitesse d'écoulement du sang. Le calcul de cette vitesse peut permettre d'exprimer le débit sanguin et voir si le cœur a un fonctionnement normal.
2.3.3. L'expansion de l'Univers
L'effet Doppler permet de voir que l'Univers est en constante expansion. C'est à l'aide de l'effet Doppler qu'Edwin Hubble, un physicien américain, a pu établir une loi a son nom, la loi de Hubble qui postule que la vitesse d'éloignement entre deux galaxies est proportionnelle à la distance qui les sépare. La constante de proportionnalité s'appelle constante de Hubble et son inverse correspond à l'âge estimé de l'Univers observable.
Théorème 1. (La loi de Hubble - HP)
Soit \(d\) la distance entre deux galaxies qui varie au cours du temps. La vitesse d'éloignement entre ces deux étoiles notée \(v\) est donnée par la relation de proportionnalité suivante :
Remarque : La constante de Hubble \(H_0\) n'est pas constante. En effet, pour que son inverse \(H_0^{-1}\) corresponde à l'âge de l'Univers, cette valeur doit varier dans le temps et de manière décroissante car l'âge de l'Univers croît. Préciser l'indice 0 permet de mettre en évidence que la valeur a été prise à l'instant où on applique la loi. On devrait plutôt parler de la fonction de Hubble notée \(H(t)\) et qui est définie comme suit : \[ H:t\mapsto \frac{v(t)}{d(t)} \] avec \(v\) et \(d\) deux fonctions du temps correspondant respectivement à la vitesse d'éloignement et à la distance entre deux galaxies.
L'effet Doppler s'applique aux ondes électromagnétiques et plus particulièrement à la lumière. L'observation des spectres d'émission d'une galaxie ou même d'une étoile ou encore d'une planète au cours du temps permet de savoir si cette dernière se rapproche ou s'éloigne.
Lorsque le spectre d'émission se décale vers la gauche autrement dit les raies d'émission se décalent vers le bleu alors cela signifie que le corps céleste se rapproche : on parle de Blueshift.
Inversement, lorsque le spectre d'émission se décale vers la droite autrement dit les raies d'émission se décalent vers le rouge alors cela signifie que le corps céleste s'éloigne : on parle de Redshift.
L'explication réside dans la formule qui régit l'effet Doppler. En se plaçant dans le référentiel géocentrique, la Terre qui nous représente (l'observateur) a une vitesse nulle donc on applique les formules sur l'effet Doppler vues en section 2. Notons d'autre part que la lumière a une vitesse très grande devant la vitesse de déplacement des objets célestes. Par exemple, c'est la formule (2) qui s'applique alors dans le cas d'un rapprochement: \[ f_r=\frac{1}{1-\beta}f_e \quad \textrm{où} \quad \beta=\frac{v}{c} \ll 1 \] où \(v\) désigne la vitesse du corps en approche et \(c\) la célérité de la lumière dans le vide.
On observe bien que dans le cas d'un rapprochement, la fréquence reçue est plus grande que la fréquence émise donc la longueur d'onde diminue d'après la relation 3 donc il y a un bien un décalage des longueurs d'onde vers les petites valeurs, c'est-à-dire un décalage vers le bleu. Le raisonnement dans le cas d'un éloignement est analogue mais dans ce cas, on utilise la relation (4).
Rappelons que le domaine du visible, c'est-à-dire la gamme des longueurs d'onde de la lumière visibles à l'oeil nu, correspond à : \[ [380 \text{ nm}, 780 \text{ nm}] \]
Remarque : Le Redshift s'observe en observant le décalage des longueurs d'onde vers la droite mais remarquons que comme \(\beta \ll 1\), cette variation est très faible. Elle dépend de la vitesse d'éloignement. C'est la même remarque pour un rapprochement mesuré avec le Blueshift.
3. Compléments - recommandé
3.1. Effet Doppler dans le cas d'un observateur en mouvement
Dans le cas où un observateur observe l'effet Doppler alors qu'il est en mouvement animé par une vitesse \(v_0\), si l'on note \(u\) la célérité de propagation des ondes émises et \(v\) la vitesse de l'émetteur alors on peut écrire les relations suivantes entre la fréquence émise \(f_e\) et la fréquence reçue \(f_r\) :
Dans le cas d'un émetteur qui s'approche de l'observateur :
Dans le cas d'un émetteur qui s'éloigne de l'observateur :
3.2. La vitesse du son
Définition 10. (Le son)
Le son correspond à l'onde mécanique progressive qui déforme localement son milieu dans lequel il se propage à cause d'une variation de la pression. Sa célérité comme toutes les ondes, dépend des caractéristiques propres au milieu dont lequel il se propage.
Remarque : Par exemple, la température et la densité du milieu interviennent dans le calcul de la vitesse du son.
Un premier modèle qui permet de modéliser la célérité du son dans un milieu assimilable à un gaz parfait est que cette célérité notée \(c\) dépend exclusivement de la température et évolue comme suit : \[ c=20,05\sqrt{T} \] où \(T\) désigne la température en Kelvins.
C'est ce modèle qu'on adopte lorsqu'on étudie la célérité du son dans l'air assimilable à un gaz parfait.
Dans un fluide, sous certaines hypothèses de réversibilité du phénomène étudié (le milieu doit retrouver son état originel), alors la célérité \(c\) du son peut être décrite par le modèle suivant : \[ c=\sqrt{\frac{1}{\chi_S\rho}} \] où \(\chi_S\) est une constante qui dépend du point où l'on calcule \(c\) appelée coefficient de compressibilité isentropique et \(\rho\) désigne la masse volumique du fluide. Dans certains exercices, ce modèle est étudié et la valeur de \(\chi_S\) est toujours donnée.
Remarque : L'eau est un fluide.
On pourrait aussi définir la célérité du son dans un milieu solide homogène. Cette propagation se fera alors suivant deux directions, la direction longitudinale et la direction transversale. Notons \(c_l\) la célérité longitudinale du son et \(c_t\) la célérité transversale du son : \[ c_l=\sqrt{\frac{E(1-\nu)}{\rho(1+\nu)(1-2\nu)}} \quad \textrm{et} \quad c_t=\sqrt{\frac{E}{2\rho(1+\nu)}} \] où les grandeurs \(E\), \(\nu\) et \(\rho\) sont des constantes correspondant respectivement au module d'Young du solide, le coefficient de Poisson du solide et \(\rho\) la masse volumique du solide.
3.3. Le nombre de Mach
Définition 11. (Le nombre de Mach)
On appelle nombre de Mach, noté \(\mathcal{M}a\), le nombre correspondant au rapport de la vitesse d'un objet notée \(v\) dans un milieu et \(c\) la célérité du son dans ce même milieu :
Remarque : Ainsi, le nombre de Mach existe dans toutes les situations étant donné qu'on peut définir la vitesse d'un objet en toutes circonstances.
Comme nous avons pu définir la célérité du son dans les trois milieux qu'on croise en général : gazeux assimilable à un gaz parfait, fluide et solide homogène. On peut peut définir le nombre de Mach dans différentes situations.
Lorsque la vitesse de l'objet est inférieure à celle du son dans le même milieu autrement dit lorsque le nombre de Mach est inférieur à 1 : on parle d'un écoulement subsonique. Dans ce cas, les ondes provoquées par le déplacement dans le milieu de l'objet sont toujours contenues dans les ondes sonores qu'il pourrait produire si on lui fixe un émetteur sonore fictif : l'effet Doppler prend naissance.
Lorsque la vitesse de l'objet est égale à la vitesse du son dans son milieu donc pour un nombre de Mach égal à 1, les ondes crées par l'objet s'accumulent à l'avant de l'objet dans un plan qui lui est perpendiculaire : on parle d'un écoulement sonique. C'est ce qui donne naissance au mur du son.
Dans le cas où l'objet se déplace plus vite que le son dans son milieu alors cela équivaut à un nombre de Mach supérieur à 1 : on parle d'un écoulement supersonique. Ainsi, les ondes sonores qui seraient potentiellement créées par un émetteur fictif qui aurait été placé sur l'objet sont contenues successivement dans un cône dont le sommet est l'objet de vitesse \(v\) : c'est le cône de Mach.
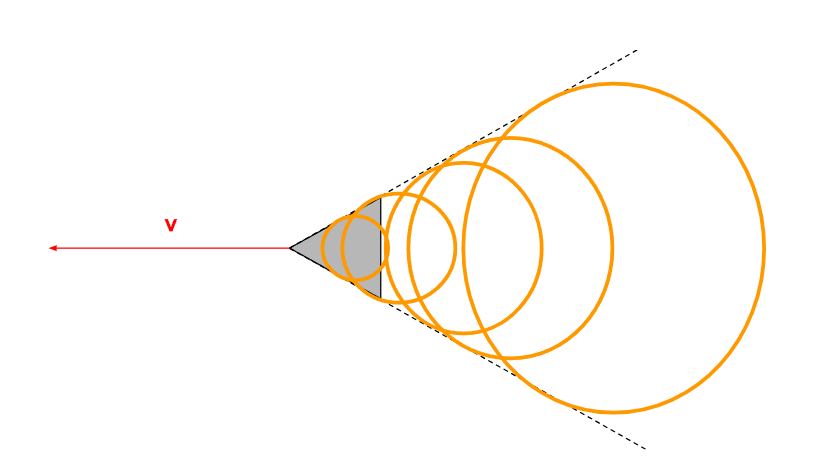
Figure 5. - Apparition du cône de Mach pour \(\mathcal{M}a>1\)
C'est pour cela que sur certaines vidéos, on voit l'apparition d'un cône à l'avant des avions de chasse qui vole à une vitesse \(v\) qui dépasse \(c\). Il y a une accumulation des ondes créées par l'avion de chasse sur l'avant du cône de Mach, ces ondes correspondent à des déplacements d'air qui se superposent.
Remarque : Le phénomène d'apparition d'un cône lorsqu'une vitesse caractéristique d'un milieu est dépassée est observable dans d'autres domaines. Dans les centrales nucléaires, dans les piscines qui contiennent les barres d'uranium, on peut voir l'apparition d'un flash lumineux de couleur bleu qui persiste le temps de quelques secondes. C'est ce qu'on appelle l'effet Tcherenkov. Ce phénomène apparaît quand une onde composée de particules chargées dépasse dans un milieu la célérité de la lumière dans ce même milieu. Dans le cas des barres d'uranium, c'est un flux d'électrons qui est émis et leur vitesse dépasse celle de la lumière dans l'eau contenue dans la piscine. Ainsi, les ondes s'accumulent à nouveau sur un cône et la couleur bleue a pour origine le milieu de propagation du phénomène.
Rappelons que la célérité de la lumière dans un milieu dépend de l'indice optique de ce dernier qu'on suppose constant pour se simplifier les calculs. On note cet indice \(n\) et on a que la célérité de la lumière dans le milieu notée \(v\) est liée à la célérité de la lumière dans le vide notée \(c\) par la relation suivante : \[ \boxed{c=nv} \] Comme \(v \leq c\) alors tout indice optique est minoré par 1, c'est-à-dire, \(n \geq 1\).
Par exemple, la vitesse de la lumière dans l'eau vaut environ \(2 \times 10^8\) m.s⁻¹. Ainsi, la vitesse de la lumière dans un milieu peut alors être dépassée tant qu'elle ne vaut pas \(c\) sans contredire les équations de la relativité d'Einstein.
4. Notion d'intensité sonore
Ici, on développe la notion d'intensité sonore. C'est la grandeur qui permet d'exprimer à quel point un son est fort ou non lorsqu'on l'entend. En revanche, lorsqu'on veut savoir si un son est aigu ou grave, on s'intéresse à sa fréquence. L'intensité sonore va nous permettre de définir les seuils d'audition et classer parmi eux ceux qui sont nocifs pour l'oreille humaine. Enfin, nous verrons différentes façons qui permettent d'atténuer le volume d'un son.
4.1. L'intensité sonore
Définition 12. (L'intensité sonore)
On appelle intensité sonore d'un son en un point \(M\), la puissance surfacique reçue en ce point. Si l'on note \(I(M)\) l'intensité sonore en \(M\), \(P(M)\) la puissance reçue en \(M\) et \(S_M\) la surface de la sphère qui a pour centre la position de l'émetteur avec \(M\) à sa surface alors, \(I(M)\) s'écrit :
Remarque : Remarquons que l'intensité sonore dépend du point \(M\) où l'on mesure cette intensité. On peut alors définir un champ scalaire lié à la grandeur \(I\) qui en \(M\) prend la valeur \(I(M)\).
De plus, observons que \(P\) est indépendant du temps mais on pourrait s'imaginer que la puissance dépende du temps. Dans ce cas, la définition s'écrit différemment : \[ I(M,t)=\frac{P(M,t)}{S_M} \] la sphère étant fixée car on suppose que l'émetteur est immobile. Sinon, si l'émetteur était en mouvement, la surface de la sphère varierait au cours du temps, ça serait également une fonction du temps.
Remarque : On parle aussi d'intensité acoustique pour parler d'intensité sonore.
4.2. Le niveau d'intensité sonore
Si l'on calculait l'intensité \(I\), on s'apercevrait que l'oreille perçoit à un son pour une intensité sonore égale à \(10^{-12}\) W.m⁻², notée \(I_0\) et appelée le seuil d'audibilité. Par ailleurs, on observerait qu'à une intensité égale à 1 W.m⁻², on atteint à un seuil critique de danger appelé le seuil de douleur.
Lorsque les valeurs s'étendent autant, on passe à l'échelle dite semi-logarithmique. On définit alors ce qu'on appelle le niveau sonore comme une normalisation logarithmique des valeurs de \(I\) par rapport à la référence \(I_0\) :
Définition 13. (Le niveau sonore)
On appelle niveau sonore, la grandeur notée \(L\) qui à partir de l'intensité \(I\) mesurée en un point \(M\) et la valeur de référence \(I_0\) renvoie :
Remarque : Comme le rapport \(\frac{I}{I_0}\) est compris entre 1 et \(10^{12}\) alors en passant au logarithme, cela permet d'avoir des valeurs comprises entre 0 et 12. Le facteur 10 permet de rendre homogène l'expression à une grandeur qui s'exprime en décibels noté dB. Ainsi, on en déduit que : \[ L\in[0,120] \] Notons que la dépendance implicite à \(M\) dans la définition précédente n'a pas été illustrée mais il est essentiel de retenir que \(L\) dépend du point choisi car \(I\) en dépend d'après la définition 12 ainsi on a de manière rigoureuse : \[ \boxed{L(M)=10\log\left(\frac{I(M)}{I_0}\right)} \] encore ici, on pourrait parler de fonction qui dépend du temps et réécrire la formule comme : \[ \boxed{L(M,t)=10\log\left(\frac{I(M,t)}{I_0}\right)} \] Attention, \(I_0\) est une constante qui ne dépend ni du point \(M\) ni du temps \(t\).
Remarque : Il est possible de retrouver l'expression de l'intensité \(I\) à partir de la valeur du niveau sonore en un point qu'on note \(M\) : \[ \boxed{I(M)=I_0\times 10^{\frac{L(M)}{10}}} \] Pour en savoir plus sur le logarithme, vous pouvez consulter le cours sur le logarithme népérien.
Cette formule est utile lorsqu'on cherche à calculer ce qu'il se passe pour le niveau sonore lorsqu'on multiplie par un certain facteur l'intensité.
Exercice.
Initialement, en un point \(M\), on mesure une intensité \(I(M)\). La puissance du son émis augmente d'un facteur multiplicatif égal à 10. On décide alors de mesurer à une distance deux fois moins proche qu'au départ l'intensité sonore du son émis par l'émetteur. Si l'on note \(N\) ce nouveau point et \(E\) la position de l'émetteur, cela revient à dire que : \[ EN=2EM \] On note \(I(N)\) cette nouvelle intensité mesurée. Déterminer de combien le niveau sonore a augmenté entre la position initiale en \(M\) avant que le volume du son augmente et la nouvelle position en \(N\) après que le volume ait été augmentée.
Correction
Si la puissance du son émis a augmenté de 10 alors cela veut dire que toutes les intensités en tous les points de l'espace ont été multipliées par 10 d'après la définition 12. Si l'on change de position et qu'on double notre distance à l'émetteur de départ, la surface de la sphère change car son rayon double par rapport à la sphère de surface \(S_M\). Ainsi, comme la variation de rayon se fait au carré dans le calcul de la surface de la sphère alors : \[ S_N=4S_M \] En effet : \(S=4\pi r^2\) avec \(S\) la surface d'une sphère de rayon \(r\). Ainsi, \[ I(N)=\frac{P(N)}{S_N}=\frac{P_{après}}{S_N}=\frac{10P_{avant}}{4S_M}=\frac{5}{2}I(M) \quad (5) \] avec \(P_{avant}\) la puissance avant que le volume augmente et \(P_{après}\) la puissance après que le volume ait augmenté.
D'après la définition 13, on a en \(N\) : \[ L(N)=10\log\left(\frac{I(N)}{I_0}\right) \] or la relation (5) permet d'écrire : \[ L(N)=10\log\left(\frac{5I(M)}{2I_0}\right) \] en développant, on obtient grâce à la définition 13 appliquée en \(M\) : \[ L(N)=L(M)+10\log\left(\frac{5}{2}\right) \] Si l'on note \(\Delta L\), la différence de niveau sonore entre \(N\) et \(M\) alors : \[ \Delta L=10\log\left(\frac{5}{2}\right)>0 \] Par application numérique, on obtient : \[ \boxed{\Delta L \approx 4 \text{ dB}} \] On répond ainsi à la question : le niveau sonore entre la position \(M\) avant que le son augmente et la position \(N\) après que le son ait été augmenté vaut environ 4dB.
L'oreille humaine perçoit un son à partir de 0 dB. Des bruits légers correspondent à un niveau sonore allant jusqu'à 40 dB ; des bruits ambiants correspondant à une sonnerie, des conversations à vois haute, des bruits de klaxon correspondent à un niveau sonore qui varie jusqu'à 80 dB. Au-delà on définit une première limite, le seuil de risque correspondant à un niveau sonore de 80 dB.
Dès 90 dB, on définit un seuil de danger où sans protection auditives, l'oreille humaine peut souffre de douleurs temporaires (marteau-piqueur, sirène, boite de nuit) et enfin, à partir de 120 dB, on atteint le seuil de douleur. Toute exposition longue (de l'ordre de la minute) favorise la perte d'audition partielle au mieux, totale dans le pire des cas. C'est ce qu'on risque lorsqu'on reste près d'un avion au décollage.
4.3. L'atténuation sonore
Pour prévenir d'un volume sonore trop élevée, on dispose de dispositifs qui permettent d'atténuer le volume entendue : on peut parler d'atténuation par absorption par exemple. Enfin, naturellement, si l'on fixe un volume constant d'un son émis par un émetteur, le volume perçue par l'oreille humaine change avec la distance à l'émetteur. C'est une conséquence de la définition 12.
L'atténuation géométrique consiste à s'éloigner d'un émetteur pour voir l'intensité sonore de l'observateur diminuer car plus on s'éloigne, plus la surface de sphère augmente par un facteur multiplicatif élevé au carré (cf. exercice précédent sur le niveau sonore).
Par exemple, si un émetteur émet un son de puissance \(P\) constante et qu'à l'état initial, on mesure une intensité \(I\) alors en s'éloignant d'une distance dix fois plus grande, l'intensité est divisée par un facteur 100 donc le niveau sonore sera diminuée de 20 dB (faire le calcul si vous n'êtes pas convaincu en utilisant le raisonnement de l'exercice précédent avec les surfaces et la définition 13).
L'atténuation par absorption consiste à mettre devant la source un obstacle d'une certaine épaisseur \(e\). Alors, il est possible de montrer que l'intensité transmise après l'obstacle dépend de l'épaisseur du matériau \(e\) et des propriétés du milieu qui le compose. C'est une conséquence logique qu'on peut discerner facilement.
Caractérisons davantage ce phénomène d'atténuation par absorption. Lorsqu'une onde sonore d'intensité \(I\) est incidente sur l'une des faces du matériau, une partie de l'onde est transmise, elle passe à travers la matériau pour donner naissance à une onde sonore d'intensité \(I_t\) appelée intensité transmise et l'autre partie de l'onde est réfléchie à sa surface donnant naissance à une onde sonore d'intensité \(I_r\) appelée intensité réfléchie.
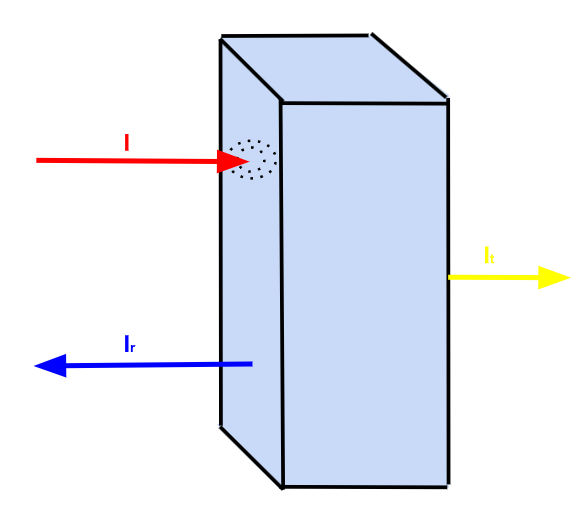
Figure 6. - Représentation du phénomène d'atténuation par absorption par un matériau
La figure 6 permet de rendre compte d'une intensité incidente notée \(I\), une intensité qui est réfléchie notée \(I_r\) et une intensité transmise qui est notée \(I_t\). Il est attendu que \(I_t < I\) quand l'épaisseur d'un matériau \(e>0\).
On définit une grandeur \(A\) qui permet de rendre compte du phénomène d'absorption, voir à quel point le matériau agit comme un obstacle qui isole des sons.
Définition 14. (L'atténuation)
On appelle atténuation, la grandeur notée \(A\) qui à partir de l'intensité incidente \(I\) et l'intensité transmise \(I_t\) s'exprime comme :
Remarque : \(A\) permet de mesurer à quel point un matériau agit comme un isolant pour le son : \(A\) est une grandeur positive ou nulle car \(I_t \leq I\). Nulle quand \(I=I_t\), le matériau agit comme s'il n'était pas : on parle de transmission idéale, sans perte d'intensité. Quand \(A>0\), on dit que la matériau bloque le son avec une certaine efficacité donnée par la valeur de \(A\). Quand \(A\rightarrow\infty\), le matériau agit comme un isolant parfait qui bloque complètement le son : aucun son ne traverse le matériau.