Terminale Spé : Exercices sur la cinématique du point matériel
La mention ❤️ indique que la méthode de résolution proposée par l'exercice est à maîtriser et à savoir refaire, on peut aussi parler d'exercice classique. Finalement, chaque exercice possède sa propre difficulté : 🌶️ pour un exercice facile, 🌶️🌶️ pour un exercice de difficulté moyenne et 🌶️🌶️🌶️ pour un exercice difficile dans sa résolution.
Exercices d'application
Exercice n°1 (Culture générale scientifique) ❤️ 🌶️ 🌶️ 🌶️
1. Par abus de langage, les notions de mouvement et de trajectoire sont souvent confondues alors qu'elles sont différentes. Définir ces deux termes.
2. Définir la notion de référentiel. Schématiquement, on ne peut pas représenter un référentiel de dimension 4 ou plus. Donner alors la dimension maximale d'un référentiel si l'on souhaitait le représenter graphiquement.
3. Donner pour chaque trajectoire suivante, un exemple de la vie réelle : trajectoire rectiligne, trajectoire circulaire, trajectoire cycloïdale et trajectoire elliptique.
Voir l'indice
1. La trajectoire est la forme géométrique (la "trace"), tandis que le mouvement décrit comment cette trace est parcourue dans le temps (vitesse, accélération).
2. Un référentiel inclut un repère d'espace (combien de dimensions ?) et un repère de temps (une horloge).
3. Pensez à un train, à la Lune, à une valve de pneu de vélo, et aux planètes.
Afficher le corrigé
1. Une trajectoire d'un système correspond à l'ensemble des positions prises successivement par le système au cours du temps. En pratique, on relie les positions entre elles pour représenter les trajectoires. Un mouvement d'un système correspond à la description du système par sa trajectoire et sa vitesse le long de cette trajectoire.
2. Un référentiel est un système composé d'un repère spatial et d'une échelle temporelle. La dimension d'un référentiel en théorie est 4, or la dimension 4 n'est pas représentable. On représente au maximum les référentiels de dimension 3 muni d'un repère spatial de dimension 2 et d'une échelle de temps de dimension 1.
3. Une trajectoire rectiligne peut correspondre au mouvement d'une bille sur un sol plat ; une trajectoire circulaire au mouvement d'une masse à l'extrémité d'un pendule ; une trajectoire cycloïdale au mouvement d'un point fixe sur une roue de vélo lorsque le vélo roule ; une trajectoire elliptique au mouvement de la Terre autour du Soleil.
Exercice n°2 (Loi de composition, en translation) ❤️ 🌶️ 🌶️ 🌶️
On considère deux référentiels, l'un noté \(\mathcal{R}\) et l'autre \(\mathcal{R}'\) de centre respectivement \(O\) et \(O'\). On se place dans le cas uniaxial (à une dimension) où l'on repère l'ensemble des grandeurs suivant l'axe \(\vec{x}\) dans le référentiel \(\mathcal{R}\) et l'axe \(\vec{x}'\) dans le référentiel \(\mathcal{R}'\). On suppose que le référentiel \(\mathcal{R}\) est galiléen et que le référentiel \(\mathcal{R}'\) est en translation par rapport au référentiel \(\mathcal{R}\) animé par une vitesse \(\vec{v}(\mathcal{R}'/\mathcal{R})=v_0(t)\vec{x}\).
1. Soit \(M\) un point de position \(x_1(t)\) dans le référentiel \(\mathcal{R}\) (\(\overrightarrow{OM}=x_1(t)\vec{x}\)) et de position \(x_2(t)\) dans le référentiel \(\mathcal{R}'\) (\(\overrightarrow{O'M}=x_2(t)\vec{x}'\)). Donner l'expression de la vitesse de \(M\) dans \(\mathcal{R}\) et dans \(\mathcal{R}'\) en fonction des dérivées \(\dot{x_1}=\frac{dx_1}{dt}\) et \(\dot{x_2}=\frac{dx_2}{dt}\).
2. En remarquant que \(\overrightarrow{OM}=\overrightarrow{OO'}+\overrightarrow{O'M}\), montrer le résultat suivant : \[ \left.\frac{d\overrightarrow{OM}}{dt}\right|_{\mathcal{R}}=\vec{v}(\mathcal{R}'/\mathcal{R})+\left.\frac{d\overrightarrow{O'M}}{dt}\right|_{\mathcal{R}'} \]
3. En déduire la relation suivante, appelée loi de composition des vitesses : \[ \boxed{\forall t, \quad \dot{x_1}(t)= \dot{x_2}(t)+v_0(t)} \]
4. Retrouver alors la loi de composition des accélérations : \[ \boxed{\forall t, \quad \ddot{x_1}(t)= \ddot{x_2}(t)+\dot{v_0}(t)} \] où \(\ddot{x_1}=\frac{d\dot{x_1}}{dt}\), \(\ddot{x_2}=\frac{d\dot{x_2}}{dt}\) et \(\dot{v_0}=\frac{dv_0}{dt}\).
Voir l'indice
Pour la Q1, la vitesse est simplement la dérivée de la position par rapport au temps dans le référentiel donné.
Pour la Q2, dérivez la relation de Chasles par rapport au temps dans \(\mathcal{R}\). Notez que la dérivée de \(\overrightarrow{O'M}\) dans \(\mathcal{R}\) n'est pas simple, mais la formule de Varignon (donnée dans l'énoncé) simplifie cela.
Pour la Q4, il suffit de dériver la loi de composition des vitesses (Q3) par rapport au temps.
Afficher le corrigé
1. On a : \[\left.\frac{d\overrightarrow{OM}}{dt}\right|_{\mathcal{R}}=\dot{x_1}\vec{x} \quad \textrm{et} \quad \left.\frac{d\overrightarrow{O'M}}{dt}\right|_{\mathcal{R'}}=\dot{x_2}\vec{x'}\]
2. En utilisant la relation de Chasles, on a : \[\left.\frac{d\overrightarrow{OM}}{dt}\right|_{\mathcal{R}}=\left.\frac{d(\overrightarrow{OO'}+\overrightarrow{O'M})}{dt}\right|_{\mathcal{R}}=\left.\frac{d\overrightarrow{OO'}}{dt}\right|_{\mathcal{R}}+\left.\frac{d\overrightarrow{O'M}}{dt}\right|_{\mathcal{R}}\] puis en remarquant que par définition : \[ \left.\frac{d\overrightarrow{O'M}}{dt}\right|_{\mathcal{R}}=\left.\frac{d\overrightarrow{O'M}}{dt}\right|_{\mathcal{R}'} \] alors on a bien : \[ \left.\frac{d\overrightarrow{OM}}{dt}\right|_{\mathcal{R}}=\vec{v}(\mathcal{R}'/\mathcal{R})+\left.\frac{d\overrightarrow{O'M}}{dt}\right|_{\mathcal{R}'} \]
3. En reprenant le résultat de la question précédente projeté sur l'axe horizontale : \[ \dot{x_1}= \dot{x_2}+v_0 \]
4. En dérivant l'égalité précédente, on retrouve facilement : \[ \ddot{x_1} = \ddot{x_2}+\dot{v_0} \]
Exercice n°3 (Volume élémentaire en coordonnées cartésiennes) 🌶️ 🌶️ 🌶️
On considère un volume élémentaire noté \(dV\) dans l'espace repéré par les coordonnées cartésiennes notées \((x,y,z)\) de dimension \(\delta x\times \delta y\times \delta z\) avec \(\delta x\) une petite distance selon l'axe des abscisses, \(\delta y\) une petite distance selon l'axe des ordonnées et \(\delta z\) une petite distance selon l'axe des côtes.
1. Justifier que ce volume est un cube.
2. On considère à présent que les dimensions du cube tendent vers 0. On utilise la notation \(dx\), \(dy\) et \(dz\) à présent au lieu de la notation \(\delta x\), \(\delta y\) et \(\delta z\). Si l'on suppose qu'à partir du volume élémentaire, on créé un cube de côté \(a\) de volume \(\mathcal{V}\) pour l'instant non connue. Justifier l'égalité suivante : \[ \mathcal{V}=\iiint_{\mathcal{V}}dV=\iiint_{\mathcal{V}} dxdydz=\left(\int_0^a dx\right)\times\left(\int_0^a dy\right)\times\left(\int_0^a dz\right) \]
3. En déduire alors que : \[ \boxed{\mathcal{V}=a^3} \]
Voir l'indice
1. Que peut-on dire de \(\delta x\), \(\delta y\), et \(\delta z\) si le volume est "élémentaire" (très petit) ? (Note : L'énoncé est un peu ambigu, on parle de cube mais les dimensions sont \(\delta x, \delta y, \delta z\). Il s'agit plus rigoureusement d'un "pavé droit élémentaire").
2. C'est une application du théorème de Fubini, qui permet de séparer une intégrale triple sur un domaine cubique (ou pavé) en un produit de trois intégrales simples.
3. Calculez \(\int_0^a dx\).
Afficher le corrigé
1. Étant donné la configuration initiale du repère cartésien, le volume engendré est un cube - nous l'illustrons avec le dessin ci-dessous :
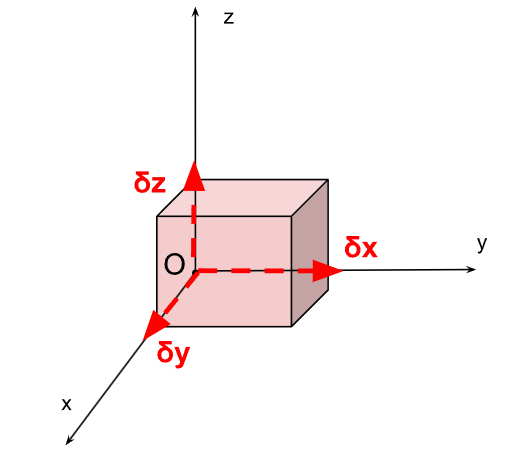
2. L'objectif est d'intégrer un volume engendré par les dimensions \(dx\), \(dy\) et \(dz\). En dimension 1, l'intégration correspond à la valeur de l'aire algébrique sous la courbe. Ici, en dimension 3, l'intégration renvoie un volume lorsque l'intégration se fait selon toutes les directions de l'espace de dimension 3, ici les axes \(\vec{x}\), \(\vec{y}\) et \(\vec{z}\). En ce qui concerne les bornes d'intégration, chaque dimension du cube est comprise entre 0 et \(a\) (cube de paramètre \(a\)). Comme les directions sont indépendantes (le produit scalaire deux à deux est nul entre chaque vecteur directeur), on peut séparer l'intégration totale entre un produit de trois intégrales simples classiquement connues. Au final, on a bien : \[ \iiint_{\mathcal{V}} dxdydz=\left(\int_0^a dx\right)\times\left(\int_0^a dy\right)\times\left(\int_0^a dz\right) \]
3. On rappelle que : \[ \int_0^a du = [u]_0^a=a-0=a \] ainsi, on en déduit de la question précédente : \[ \mathcal{V}=a^3 \]
En route vers le supérieur
Exercice n°4 (Étude d'un changement de système de coordonnées) 🌶️ 🌶️ 🌶️
L'objectif de cet exercice est d'étudier un autre système de coordonnées autre que le système de coordonnées cartésien : le système de coordonnées cylindriques.
1. On considère un point \(M\) dans l'espace repéré par ces coordonnées en cartésien \((x,y,z)\) dans le repère \((O,\vec{e_x},\vec{e_y},\vec{e_z})\). Calculer : \[ \overrightarrow{OM}\cdot\vec{e_x} \quad ; \quad \overrightarrow{OM}\cdot\vec{e_y} \quad ; \quad \overrightarrow{OM}\cdot\vec{e_z} \] où \(\cdot\) désigne le produit scalaire.
2. On pose \(r^2=x^2+y^2\). Montrer qu'il existe un réel \(\theta\) tel que : \[ x=r\cos(\theta) \quad ; \quad y=r\sin(\theta) \quad ; \quad z=z \]
3. Justifier alors qu'il est possible de passer du paramétrage par les variables \((x,y,z)\) aux variables \((r,\theta,z)\).
4. On définit alors le repère \((O,\vec{e_r},\vec{e_\theta},\vec{e_z})\) pour repérer avec les coordonnées \((r,\theta,z)\) le point \(M\). On pose : \[ \vec{e_r}=\cos(\theta)\vec{e_x}+\sin(\theta)\vec{e_y} \quad \textrm{et} \quad \vec{e_\theta}=\sin(\theta)\vec{e_x}-\cos(\theta)\vec{e_y} \] Représenter ce repère pour un point \(M\) de coordonnées \((r,\theta,z)\).
5. Démontrer les relations fondamentales suivantes : \[ \frac{d\vec{e_r}}{dt}=\dot{\theta}\vec{e_\theta} \quad ; \quad \frac{d\vec{e_\theta}}{dt}=-\dot{\theta}\vec{e_r} \quad \textrm{et} \quad \frac{d\vec{e_z}}{dt}=0 \] avec \(\dot{\theta}=\frac{d\theta}{dt}\). On rappelle que \(r\) et \(\theta\) sont des fonctions du temps.
6. Justifier du fait qu'on ait : \[ \overrightarrow{OM}=r\vec{e_r}+z\vec{e_z} \]
7. En posant \(\dot{r}=\frac{dr}{dt}\), montrer que la vitesse \(\vec{v_M}\) est de la forme : \[ \vec{v_M}(t)=\frac{d\overrightarrow{OM}}{dt}=\dot{r}\vec{e_r}+r\dot{\theta}\vec{e_\theta}+\dot{z}\vec{e_z} \]
8. En déduire l'expression de l'accélération : \[ \vec{a_M}(t)=\frac{d\vec{v_M}}{dt}=(\ddot{r}-r\dot{\theta}^2)\vec{e_r}+(2\dot{r}\dot{\theta}+r\ddot{\theta})\vec{e_\theta}+\ddot{z}\vec{e_z} \]
9. On suppose que le point \(M\) a pour coordonnée radiale, une constante, c'est-à-dire que \(r\) ne dépend plus du temps et une cordonnée en altitude nulle donc \(z=0\). Dans ce cas, que valent les termes \(\dot{r}\), \(\dot{z}\), \(\ddot{r}\) et \(\ddot{z}\) ? En déduire alors que l'accélération de \(M\) peut se récrire comme : \[ \vec{a_M}(t)=-r\dot{\theta}^2\vec{e_r}+r\ddot{\theta}\vec{e_\theta} \]
10. En exprimant \(v_M(t)=||\vec{v_M}(t)||\) en fonction de \(r\) et de \(\dot{\theta}\), en déduire que l'accélération peut s'écrire : \[ \vec{a_M}(t)=-\frac{v_M^2(t)}{r}\vec{e_r}+\frac{dv_M(t)}{dt}\vec{e_\theta} \]
11. En introduisant les vecteurs unitaires \(\vec{n}=-\vec{e_r}\) et \(\vec{t}=\vec{e_\theta}\), montrer que l'on vient d'établir l'expression de l'accélération dans la base de Frenet.
12. Exprimer le déplacement élémentaire \(\overrightarrow{dl_M}=d\overrightarrow{OM}\) en fonction de \(\vec{v_M}\) et \(dt\). Montrer d'abord qu'en coordonnées cartésiennes, il prend cette forme : \[ \overrightarrow{dl_M}=dx\vec{e_x}+dy\vec{e_y}+dz\vec{e_z} \] puis, prouver qu'en coordonnées cylindriques, il s'écrit comme suit : \[ \overrightarrow{dl_M}=dr\vec{e_r}+rd\theta\vec{e_\theta}+dz\vec{e_z} \]
Théorème : S'il existe un triplet \((a,b,c)\) tel que le déplacement élémentaire \(\overrightarrow{dl_M}\) s'écrit dans un repère de la forme \((O,\vec{e_a},\vec{e_b},\vec{e_c})\) : \(\overrightarrow{dl_M}=da\vec{e_a}+db\vec{e_b}+dc\vec{e_c}\) alors le volume élémentaire dans ce système de coordonnées, noté \(dV\), s'exprime comme suit : \[ dV=da\times db\times dc \]
13. Retrouver l'expression du volume élémentaire \(dV\) de l'exercice précédent : \[ dV=dxdydz \]
14. Avec le même principe, déterminer l'expression du volume élémentaire \(dV\) en coordonnées cylindriques.
15. On suppose que la coordonnée radiale est bornée (comprise) entre \(0\) et \(R\) avec \(R\) une constante positive, que la coordonnée angulaire est bornée entre \(0\) et \(2\pi\) et enfin, on suppose que \(z\) est bornée entre \(0\) et \(H\) où \(H\) est aussi une constante positive. On cherche alors à calculer le volume du cylindre de rayon \(R\) et de hauteur \(H\). Montrer que ce volume notée \(\mathcal{V}\) est donnée par : \[ \mathcal{V}=\iiint_\mathcal{V} dV=\left(\int_{0}^R rdr\right)\times \left(\int_0^{2\pi} d\theta \right) \times \left(\int_0^H dz\right) \]
16. En déduire alors que : \[ \mathcal{V}=\pi R^2H \]
17. Le système de coordonnées sphériques est repéré par \((O,\vec{e_r},\vec{e_\theta},\vec{e_\varphi})\) avec les coordonnées \((r,\theta,\varphi)\). Le déplacement élémentaire s'écrit : \[ \overrightarrow{dl_M}=dr\vec{e_r}+rd\theta\vec{e_\theta}+r\sin(\theta)d\varphi \vec{e_\varphi} \] On considère que \(r\) est compris entre \(0\) et \(R\), \(\theta\) est compris entre \(0\) et \(\pi\) et \(\varphi\) est compris entre \(0\) et \(2\pi\). A l'aide d'un raisonnement détaillé, montrer que le volume, noté \(\mathcal{V}\), d'une sphère de rayon \(R\) est égal à : \[ \mathcal{V}=\frac{4}{3}\pi R^3 \]
Voir l'indice
Q5: Dérivez \(\vec{e_r}\) et \(\vec{e_\theta}\) par rapport au temps en utilisant la dérivation en chaîne (ex: \(\frac{d(\cos\theta)}{dt} = \frac{d(\cos\theta)}{d\theta} \times \frac{d\theta}{dt} = -\sin(\theta) \dot{\theta}\)).
Q7 & Q8: Appliquez la formule de dérivation d'un produit \((u \cdot v)' = u'v + uv'\). N'oubliez pas que \(r\), \(\theta\), \(z\), \(\vec{e_r}\) et \(\vec{e_\theta}\) dépendent tous du temps !
Q12: Par définition, \(\vec{v_M} = \frac{d\overrightarrow{OM}}{dt} = \frac{\overrightarrow{dl_M}}{dt}\). Donc \(\overrightarrow{dl_M} = \vec{v_M} dt\). Utilisez le \(\vec{v_M}\) de la Q7.
Q14, 15, 17: Pour le volume élémentaire \(dV\), multipliez les composantes du déplacement élémentaire \(\overrightarrow{dl_M}\). Pour le volume total, intégrez \(dV\) sur les bornes données.
Exercice n°5 (Autour de la quantité de mouvement) 🌶️ 🌶️ 🌶️
On considère la situation suivante : on considère deux billes, l'une verte et l'autre rouge. La bille verte est initialement au repos et on lance selon une trajectoire rectiligne la bille rouge vers la bille verte à une vitesse constante de 5 m.s⁻¹. On suppose aussi que la bille rouge est deux fois plus lourde que la bille verte.
Déterminer la valeur de la vitesse de la bille rouge après l'impact.
Voir l'indice
Cet exercice est un "choc élastique". En l'absence de forces extérieures, la quantité de mouvement totale du système {bille 1 + bille 2} se conserve. De plus, pour un choc "élastique", l'énergie cinétique totale se conserve également. Vous avez deux équations et deux inconnues (les vitesses finales des deux billes).
Exercice n°6 (Paradoxe d'Achille et de la tortue) 🌶️ 🌶️ 🌶️
Le paradoxe d'Achille et de la tortue, formulé par Zénon d'Élée, dit qu'un jour, le héros grec Achille a disputé une course à pied avec une tortue. Comme Achille était réputé être un coureur très rapide, il avait accordé gracieusement au lent reptile une avance de cent mètres.
L'argument exposé par Zénon est qu'Achille ne pourra pas rattraper la tortue [...], car pendant qu'Achille court jusqu'au point d'où a démarré la tortue, cette dernière avance, de telle sorte qu'Achille ne pourra jamais annuler l'avance de l'animal.
[...] Nous allons démontrer que ce paradoxe est faux [...].
Dans toute la suite, nous nous plaçons suivant un seul axe repéré par \(x\). On suppose que la tortue part avec 100 m d'avance à une vitesse de \(5\) m.s⁻¹. On suppose qu'Achille court à la vitesse de 10 m.s⁻¹.
1. Déterminer les équations horaires du mouvement de la tortue notée \(x_T(t)\) et d'Achille notée \(x_A(t)\).
2. Déterminer le temps \(T\) au bout duquel Achille pourra rattraper la tortue.
3. Soit \(i\in\mathbb{N}\). On définit les instants \(t_i\) comme les durée au bout duquel Achille arrive à rattraper l'avancée prise par la tortue. Calculer les trois premiers termes de la suite \((t_i)_{i\in\mathbb{N}}\).
4. Montrer alors que le temps \(T\) au bout duquel Achille croise enfin la tortue est donné par : \[ T=\sum_{n=0}^\infty \frac{10}{2^n}=10+5+2,5+1,25+... \]
5. Soit \(n\in\mathbb{N}^*\). Montrer en développant le terme de droite que si \(x\) et \(y\) sont des réels alors, \[ x^n-y^n=(x-y)\sum_{k=0}^{n-1}x^ky^{n-1-k} \]
6. En déduire alors que si \(x\ne1\), l'identité suivante est vraie : \[ \sum_{k=0}^{n-1}x^k=\frac{1-x^n}{1-x} \]
7. Justifier alors que si \(0<x<1\) alors :
\[ \sum_{k=0}^{n-1}x^k \xrightarrow[n\to\infty]{} \frac{1}{1-x} \]On vient d'établir que :
\[ \forall x\in\mathbb{R}, \quad \textrm{si } |x|<1 \textrm{ alors }\sum_{n=0}^{\infty}x^n = \frac{1}{1-x} \]8. En utilisant le résultat précédent, en déduire la valeur de \(T\) sous sa forme obtenue à la question 4.
Voir l'indice
Q1: Équation horaire d'un mouvement rectiligne uniforme : \(x(t) = v \cdot t + x_0\). N'oubliez pas l'avance de 100m pour la tortue.
Q2: Achille rattrape la tortue lorsque \(x_A(t) = x_T(t)\). Résolvez l'équation.
Q4 & Q8: Identifiez la série géométrique. \(T = \sum_{n=0}^\infty 10 \cdot (\frac{1}{2})^n\). C'est une somme de la forme \(C \sum x^n\). Utilisez la formule de la Q7.
Exercice n°7 (Étude de cas de la fusée) 🌶️ 🌶️ 🌶️
On considère une fusée de masse \(M_0\) à vide (sans carburant) et de masse \(M\) après son approvisionnement en carburant. On s'intéresse à la phase de décollage. Au moment du décollage, la fusée éjecte à une vitesse constante \(v\) le fuel sous forme de gaz. À partir des données de l'énoncé, calculer la vitesse la fusée notée \(v_f\) après l'éjection de tout le fuel contenu dans la fusée.
On représente la situation comme suit :
.png)
FIGURE 1 - Schéma d'une fusée éjectant son fuel sous forme de gaz
Voir l'indice
Cet exercice est une application directe de la conservation de la quantité de mouvement (vue dans la section 2.4). Considérez le système {Fusée + Gaz} comme isolé. La quantité de mouvement totale avant l'éjection (vitesse nulle) doit être égale à la quantité de mouvement totale après l'éjection (fusée dans un sens, gaz dans l'autre).
Exercice n°8 (Le facteur de Lorentz) 🌶️ 🌶️ 🌶️
La théorie de Newton propose une description quantitative de la gravitation mais peu qualitative par rapport à la théorie d'Einstein. [...] Einstein a [...] postulé que tout objet ne peut aller plus vite que la vitesse de la lumière dans le vide (\(c=3.10^8\) m.s⁻¹). Il introduit aussi un facteur, appelé facteur de Lorentz qui tient compte des effets relativistes [...].
On note \(\gamma\) le facteur de Lorentz et il s'exprime comme suit : \[ \boxed{\gamma=\frac{1}{\sqrt{1-\left(\frac{v}{c}\right)^2}}} \] Ainsi, si l'on note \(T\) et \(L\) respectivement la durée mesurée et la longueur observée lorsque le système est au repos alors on peut établir que : \[ T'=\gamma T \quad \textrm{et} \quad L'=\gamma L \] avec \(T'\) et \(L'\) respectivement la durée ressentie et la longueur perçue lorsque le système est en mouvement.
1. Montrer que dans le cas d'une voiture en déplacement, le facteur de Lorentz est équivalent à 1.
2. Montrer que dans le cas d'un électron se déplaçant à une vitesse \(v=0.1c\), \(L'\approx L\) et \(T'\approx T\).
3. A partir du résultat, retrouver la conclusion de la phrase de l'énoncé en italique.
4. Déterminer la valeur minimale de la vitesse \(v\) qu'on note \(v_0\) de telle façon à que l'on ait un facteur de Lorentz supérieur ou égale à 100. On exprimera le résultat \(v_0\) en fonction de \(c\).
5. On considère une voiture qui se déplace à une vitesse de 100 km.h⁻¹. On suppose que la voiture est capable de fixer une maison lointaine de longueur réelle \(L=10\) m. Quelle est la longueur perçue de la maison par les passagers de la voiture ? On exprimera l'écart \(\Delta L=L'-L\) dans les unités appropriées.
6. Un chronomètre fictif attaché à un électron dans l'espace animé d'une vitesse \(v=0.9c\) mesure une expérience faite sur Terre. Depuis l'électron, l'expérience aura duré \(1\) ms. Déterminer la durée de l'expérience faite sur Terre observée par des humains à la surface de la Terre.
Pour terminer, étudions l'importance de prendre en compte pour des vitesses élevées, les effets relativistes [...]. Prenons le cas des muons. Les muons sont des particules cosmiques formées dans la partie haute de l'atmosphère (\(z=10\) km) à partir du rayonnement solaire qui se déplace à la vitesse \(v=0,999c\). Leur durée de vie a été mesurée en laboratoire - elle est de 2,2 µs.
7. Sans prise en compte du facteur de Lorentz, montrer que les muons devraient se désintégrer en haute atmosphère, à une altitude \(z\approx9,3\) km.
8. En utilisant le facteur de Lorentz, montrer que le muon a bien le temps de traverser toute l'atmosphère avant de désintégrer. Dans le référentiel lié au muon (immobile alors dans ce dernier), déterminer la longueur perçue qu'il observe de notre atmosphère.
9. Dans son référentiel, quelle est la durée de vie réelle d'un muon animé par une vitesse \(v=0,999c\).
Voir l'indice
Q1 & Q2: Calculez le rapport \(v/c\). Si \(v \ll c\), alors \((v/c)^2 \approx 0\) et \(\gamma \approx 1\).
Q4: Posez \(\gamma = 100\) et isolez \(v/c\).
Q6: Attention au référentiel ! La durée "réelle" de l'expérience est \(T\) (mesurée sur Terre). La durée "perçue" par l'électron en mouvement est \(T' = \gamma T\). On vous donne \(T'\).
Q7 (Muons): Calculez la distance \(d = v \times T\) parcourue par le muon pendant sa durée de vie \(T = 2,2\) µs. Comparez cette distance à l'épaisseur de l'atmosphère.
Q8 (Muons): Du point de vue de la Terre, la durée de vie du muon est dilatée : \(T' = \gamma T\). Calculez cette nouvelle durée de vie et la distance \(d' = v \times T'\) qu'il peut parcourir.