Tale Spécialité : Physique : Cinématique du point matériel
📚 Table des matières
1. Préliminaires
1.1. Notion de référentiel
Définition 1. (Référentiel)
Un référentiel est un repère d'étude relatif à l'observateur muni de repères spatial et temporel.
Remarque : Il est clair qu'il nous faut une interprétation de la définition précédente. Un référentiel permet d'étudier le mouvement d'un système fixé au départ. Pour cela, il nous faut décrire sa trajectoire dans le temps. Ainsi, il est vital d'avoir à la fois un repère qui décrit dans l'espace la trajectoire de notre système mais aussi un suivi temporel car on décrit dans l'espace une évolution qui est temporelle (dépend du temps). Précisons qu'être un repère temporel, c'est de disposer une horloge en tout point de notre repère spatial. Notons qu'elles seront toutes supposées synchronisées entre elles. En quelque sorte, un référentiel « possède » 4 axes.
Figure 1. - Représentation pratique d'un référentiel
1.2. Exemples de référentiels à connaître
En exercice, on définit d'abord le système que l'on veut étudier puis le référentiel dans lequel on étudie son mouvement. Ici, on propose quelques exemples de référentiels à connaître et qu'on utilise en exercice.
Définition 2. (Référentiel héliocentrique)
Le référentiel héliocentrique est le référentiel dont le repère d'espace a son point d'origine au centre de masse du Soleil et ses axes qui pointent vers trois étoiles lointaines.
Remarque : En pratique, on utilise comme référentiel le référentiel héliocentrique lorsqu'on étudie le mouvement d'objets autour du Soleil. Par exemple, pour étudier le mouvement de la Terre autour du Soleil, on se place dans le référentiel héliocentrique. De manière similaire, pour étudier le mouvement des satellites dans le système solaire par rapport au Soleil, on utilise à nouveau ce référentiel.
Définition 3. (Référentiel géocentrique)
Le référentiel géocentrique est le référentiel dont le repère d'espace a son point d'origine au centre de masse de la Terre et a ses axes qui pointent vers trois étoiles lointaines. En général, ce sont les mêmes axes que ceux qu'on utilise pour définir le référentiel héliocentrique.
Remarque : En pratique, on utilise comme référentiel le référentiel géocentrique lorsqu'on étudie le mouvement d'objets autour de la Terre. Par exemple, pour étudier le mouvement de la Lune autour de la Terre, on se place dans le référentiel géocentrique. De manière similaire, pour étudier le mouvement des satellites envoyés depuis la Terre autour de la Terre, on se place à nouveau dans ce référentiel.
Définition 4. (Référentiel terrestre)
Le référentiel terrestre est le référentiel dont le repère d'espace a comme point d'origine, un point à la surface de la Terre et a ses axes qui pointent respectivement vers le nord, vers l'est et enfin vers le haut à la vertical locale.
Remarque : En pratique, on utilise comme référentiel le référentiel terrestre lorsqu'on étudie le mouvement d'objets à la surface de la Terre pour des altitudes atteintes très faibles. Par exemple, pour étudier le lancer d'un ballon de foot, on se place dans le référentiel terrestre.
2. Description d'un mouvement
Notons \(\mathcal{R}\) un référentiel quelconque. On le munit d'une origine \(O\) et de trois axes portés par les vecteurs unitaires \(\vec{e}_x,\vec{e}_y\) et \(\vec{e}_z\). Si l'on notait \(\vec{e}_t\) le vecteur unitaire suivant l'axe des temps alors on pourrait écrire : \[ \mathcal{R}=\left(0,\vec{e}_x,\vec{e}_y,\vec{e}_z,\vec{e}_t\right) \] D'autre part, notons \(\mathcal{S}\) le système que l'on étudie.
Définition 5. (Hypothèse du point matériel)
L'hypothèse du point matériel suppose qu'il est possible de réduire tout système de volume \(V\) à un nouveau système intermédiaire réduit à un point de volume nul et de même masse lorsque le système ne subit aucune rotation. On parle alors de système réduit à un point matériel de même masse. Le point n'est pas choisi au hasard, il correspond au centre de gravité du système étudié.
Remarque : En général, au lycée, on oublie les rotations des systèmes étudiés ainsi les réduire à des points matériels sera toujours possible. Plus généralement, étudier notre système comme un point matériel revient à étudier seulement son mouvement de translation dans le référentiel d'étude qui correspond de manière équivalent au mouvement de translation de son centre de gravité. Pour étudier ses rotations, il nous faudra le considérer comme un solide à part entière. C'est l'objet du programme de première année en mécanique après le BAC. En exercice, le point matériel sera toujours le centre de gravité du système choisi.
D'après la définition 5, on peut ramener \(\mathcal{S}\) à un point matériel de même masse notée \(m\) car on étudie que son mouvement de translation. Notons \(M\) ce point dans le référentiel \(\mathcal{R}\).
2.1. Vecteur position
Le vecteur position du système \(\mathcal{S}\) permet de rendre compte de la position du point \(M\) dans le référentiel \(\mathcal{R}\). On note traditionnellement \(\overrightarrow{OM}\) ce vecteur. On notera pour des raisons de rigueur que l'écriture du vecteur position dépend du référentiel choisi et donc \(\overrightarrow{OM}\) pourrait aussi se réécrire \(\overrightarrow{OM}_{/\mathcal{R}}\) car il dépend explicitement de \(\mathcal{R}\). On gardera pour la suite la première notation.
Comme on veut écrire \(\overrightarrow{OM}\) dans \(\mathcal{R}\), il existe les composantes \(x,y\) et \(z\) telles que :
Figure 2. - En bleu, le vecteur position \(\overrightarrow{OM}\)
2.2. Vecteur vitesse
Le vecteur vitesse correspond à la dérivée du vecteur position \(\overrightarrow{OM}\) dans le référentiel \(\mathcal{R}\). On note \(\vec{v}\) ce vecteur mais encore une fois, ce dernier est écrit seulement dans le référentiel \(\mathcal{R}\). Ainsi, les notations \(\vec{v}\) et \(\vec{v}_{/\mathcal{R}}\) sont équivalentes. Son expression est donnée par la formule suivante : \[ \vec{v}=\left. \frac{d\overrightarrow{OM}}{dt} \right| _{\mathcal{R}}=\left. \frac{dx}{dt} \right| _{\mathcal{R}}\vec{e}_x+\left. \frac{dy}{dt} \right| _{\mathcal{R}}\vec{e}_y+\left. \frac{dz}{dt} \right| _{\mathcal{R}}\vec{e}_z \] Généralement, par abus de notation, on ne précise plus le rôle joué par \(\mathcal{R}\) dans la dérivée. C'est de cette façon qu'on retrouve la formule mieux connue :
2.3. Vecteur accélération
Le vecteur accélération correspond à la dérivée seconde du vecteur position \(\overrightarrow{OM}\) (on dérive deux fois) dans le référentiel \(\mathcal{R}\). On note \(\vec{a}\) ce vecteur mais encore une fois, ce dernier est écrit seulement dans le référentiel \(\mathcal{R}\). Ainsi, les notations \(\vec{a}\) et \(\vec{a}_{/\mathcal{R}}\) sont équivalentes. Son expression simplifiée est donnée par la formule suivante :
2.4. La quantité de mouvement
On définit une nouvelle grandeur appelée vecteur quantité de mouvement ou encore vecteur impulsion notée \(\vec{p}\) qui permet de réaliser des bilans de conservation. Encore une fois ce dernier n'est pas universel, il dépend du référentiel choisi. Il suffit de s'en convaincre en observant son écriture en coordonnées cartésiennes (celles choisies depuis de le début pour décrire le mouvement du système \(\mathcal{S}\)) :
Exercice.
On considère une fusée de masse \(M_0\) à vide (sans carburant) et de masse \(M\) après son approvisionnement en carburant. On s'intéresse à la phase de décollage. Au moment du décollage, la fusée éjecte à une vitesse constante \(v\) le fuel sous forme de gaz. À partir des données de l'énoncé, calculer la vitesse la fusée notée \(v_f\) après l'éjection de tout le fuel contenu dans la fusée.
Correction
Ici, on va devoir utiliser le principe de conservation de la quantité de mouvement au cours du temps sur le système isolé {fusée+carburant+gaz} (isolé car les forces entre elles s'opposent). Si l'on note \(\vec{p}\) l'impulsion du gaz éjecté et \(\vec{p}_f\) l'impulsion de la fusée après que tout le gaz fut éjecté alors ce principe permet d'écrire : \[ \vec{p}_{final}=\vec{p}+\vec{p}_f=\vec{0}=\vec{p}_{initial} \]
En effet, à l'état initial, le système {fusée+gaz} est au repos donc de quantité de mouvement nulle. À tout autre instant, la fusée est en mouvement et le gaz aussi. Le principe de conservation permet d'écrire alors que la quantité de mouvement à l'état initial coïncide avec celle à tout autre instant.
D'après la définition de la quantité de mouvement, on en déduit que : \[ (M-M_0)\vec{v}+M_0\vec{v}_f=\vec{0} \] On en conclut finalement que : \[ \vec{v}_f=-\frac{(M-M_0)}{M_0}\vec{v}=\left(1-\frac{M}{M_0}\right)\vec{v} \] Ce résultat est cohérent avec ce que l'on pourrait observer dans la vraie vie. Il est bien entendu logique que \(M>M_0\) car la fuel a une masse positive, tandis que le gaz est éjecté vers le bas, la fusée est propulsée vers le haut. On résume cela avec le schéma suivant :
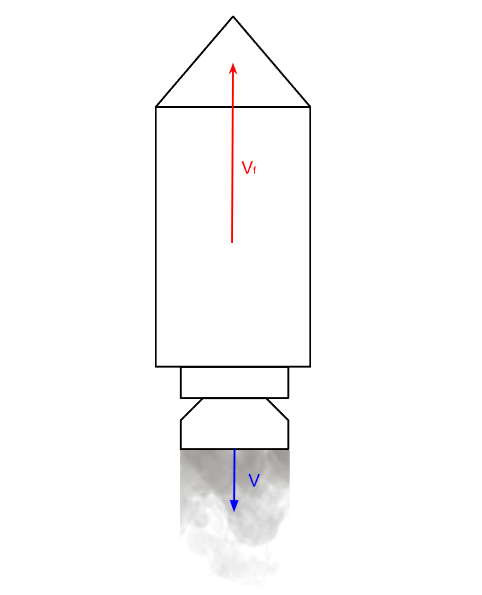
Figure 3. - Schéma d'une fusée éjectant son fuel sous forme de gaz
3. Approche graphique du calcul
Comment grâce à un suivi photo des positions d'un mobile \(M\), peut-on retrouver les vecteurs vitesse et accélération ? C'est l'objet de cette section.
Définition 6. (Chronophotographie)
On appelle chronophotographie une photo qui représente une succession des positions d'un mobile au cours du temps. Cette mesure est discrète, c'est-à-dire que les positions sont mesurées à des temps fixés et non pas de manière continue.
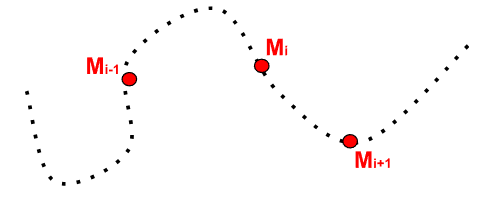
Figure 4. - Exemple de chronophotographie partielle d'un mobile \(M\)
Prenons comme exemple le mobile \(M\) de la figure 4. Nous allons chercher à tracer la vitesse de \(M\) à la position \(M_i\) notée \(\vec{v}_i\) et son accélération au même point notée \(\vec{a}_i\). Reprenons la définition de dérivée d'une fonction : \[ \vec{v}_i=\frac{d\overrightarrow{OM}}{dt}=\lim\limits_{dt \to 0} \frac{\overrightarrow{OM}(t+dt)-\overrightarrow{OM}(t)}{dt}= \frac{\overrightarrow{OM}(t+\Delta t)-\overrightarrow{OM}(t)}{\Delta t} \] On a pris \(\Delta t\) car ce sont des mesures de positions à des intervalles de temps petites et en général réguliers. \[ \vec{v}_i=\frac{\overrightarrow{OM}(t+\Delta t)-\overrightarrow{OM}(t)}{\Delta t}=\frac{\overrightarrow{OM}(t+\Delta t)-\overrightarrow{OM}(t-\Delta t)}{2\Delta t} \] En développant chacun des termes de ce résultat, on peut écrire : \[ \overrightarrow{OM}(t+\Delta t)=\overrightarrow{OM_{i+1}} \] \[ \overrightarrow{OM}(t-\Delta t)=\overrightarrow{OM_{i-1}} \] d'où, d'après la relation de Chasles : \[ \overrightarrow{OM}(t+\Delta t)-\overrightarrow{OM}(t-\Delta t)=\overrightarrow{OM_{i+1}}-\overrightarrow{OM_{i-1}}=\overrightarrow{OM_{i+1}}+\overrightarrow{M_{i-1}O}=\overrightarrow{M_{i-1}M_{i+1}} \] C'est ainsi qu'on conclut de la manière suivante :
De la même manière, on démontre que si on a les vitesse en \(M_{i-1}\) et en \(M_{i+1}\) alors on peut calculer \(\vec{a}_i\) grâce à la relation suivante :
4. Les différents types de mouvement
4.1. Le mouvement rectiligne
Définition 7. (Mouvement rectiligne)
On appelle mouvement rectiligne un mouvement dont la trajectoire est une droite ou une portion de droite.
Remarque : Si la vitesse du système est constante au cours du temps, on parle de mouvement rectiligne uniforme. S'il possède une accélération constante positive au cours du temps, on parle de mouvement uniformément accéléré et si l'accélération est constante négative au cours du temps, on parle de mouvement uniformément ralenti.
4.2. Le mouvement curviligne
Définition 8. (Mouvement curviligne)
On appelle mouvement curviligne un mouvement dont la trajectoire est une courbe ou une portion de courbe.
Ici, on pourrait décrire les mêmes constats que dans la paragraphe § 4.1. mais ici, intéressons nous à un mouvement curviligne particulier : le mouvement circulaire.
Définition 9. (Mouvement circulaire)
On appelle mouvement circulaire un mouvement dont la trajectoire est un cercle.
Pour décrire un tel mouvement, on se place dans un nouveau repère : le repère de Frenet. L'intérêt d'introduire un nouveau repère permettra de décrire plus facilement les mouvements circulaires qui, en coordonnées cartésiennes, sont plus complexes à étudier (apparition de termes trigonométriques).
Définition 10. (Repère de Frenet)
On appelle repère de Frenet le repère plan dont l'origine peut être mobile au cours du temps possédant deux axes, l'un porté par la vecteur unitaire tangentiel (ou orthoradial) noté \(\vec{t}\) et l'autre porté par le vecteur unitaire normal (ou radial) noté \(\vec{n}\) avec \(\vec{t}\) et \(\vec{n}\) orthogonaux entre eux.
Dans ce repère, on peut rendre la vitesse toujours colinéaire au vecteur tangentiel si l'on fait bien varier l'origine.
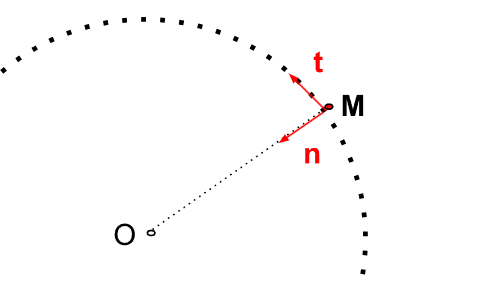
Figure 5. - Repère de Frenet placé pour étudier un mobile \(M\) de mouvement circulaire
Elles seront admises mais se démontrent très facilement en partant de ce qu'on appelle le système de coordonnées cylindriques, ce sont les expressions des vecteurs position, vitesse et accélération d'un mobile possédant un mouvement circulaire.
Si l'on note \(R\) le rayon constant de la trajectoire alors on a les formules suivantes :
Remarque : Ici, on observe un résultat critique, l'accélération ne s'exprime plus comme la simple dérivée de la vitesse. Il y a un terme de correction qui s'ajoute suivant le vecteur normal. Dans le système de coordonnées cartésiennes, les formules de la section 2 sont valables mais pas dans tous les autres systèmes de coordonnées.
Cette écriture est utile lorsqu'on veut étudier (voire indispensable à ce niveau) le mouvement des satellites autour de planètes. Par exemple, étudier le mouvement du satellite Io autour de Jupiter, le mouvement de la Terre autour du Soleil ou encore le mouvement de l'ISS autour de la Terre.
Un cas particulier de mouvement circulaire est le mouvement circulaire uniforme où la vitesse de norme \(v\) est constante donc sa dérivée temporelle est nulle et l'expression de l'accélération devient finalement :
Exercice.
L'objectif de cet exercice est d'établir une des relations les plus importantes en astronomie, la troisième loi de Kepler. On cherche à étudier le mouvement d'un satellite \(\mathcal{S}\) de masse \(m\) qui autour du Soleil a un mouvement circulaire. On suppose que le satellite n'est soumis qu'à la force gravitationnelle qu'exerce sur lui le Soleil. Dans toute la suite, \(a\) désignera le rayon de la trajectoire du satellite autour du Soleil, \(T\) le temps de parcours de l'orbite par le satellite, \(G\) la constante universelle gravitationnelle et \(M_\odot\) la masse du Soleil.
HYPOTHÈSE : On supposera que le référentiel héliocentrique est galiléen (cf. cours sur la dynamique du point matériel).
1. Définir le système que l'on étudie puis le référentiel adapté à notre étude.
2. En appliquant le principe fondamental de la dynamique, montrer que la vitesse du satellite sur son orbite est constante au cours du temps.
3. En utilisant à nouveau le principe fondamental de la dynamique, déterminer l'expression de la vitesse notée \(v\) du satellite sur son orbite.
4. En déduire l'égalité suivante appelée troisième loi de Kepler : \[ \frac{T^2}{a^3}=\frac{4\pi^2}{GM_\odot} \]
Correction
1. Le système que l'on étudie correspond au satellite. On se place dans le référentiel héliocentrique.
2. D'après le principe fondamental de la dynamique (PFD) appliqué au satellite dans le référentiel héliocentrique supposé galiléen, on peut écrire : \[ m\vec{a}=\vec{F}_g \] où \(\vec{a}\) est l'accélération du système et \(\vec{F}_g\) la force gravitationnelle subie par le satellite par le Soleil. On a aussi : \[ m\left(\frac{dv(t)}{dt}\vec{t}+\frac{v^2(t)}{a}\vec{n}\right)=G\frac{mM_\odot}{a^2}\vec{n} \] C'est le PFD écrit dans le repère de Frenet.
Par identification, on en déduit le système suivant : \[ \left \{ \begin{array}{c @{=} c} \frac{dv(t)}{dt} & 0 \\ \frac{v^2(t)}{a} & G\frac{M_\odot}{a^2} \end{array} \right. \] Comme \(\frac{dv(t)}{dt}=0\) alors \(v\) est une constante au cours du temps.
3. En reprenant la question 2, la seconde égalité du système permet d'écrire : \[ v=\sqrt{\frac{GM_\odot}{a}} \] Il est intéressant de savoir que cette vitesse ressemble à la première vitesse cosmique, c'est la vitesse qu'un satellite lancé depuis la Terre doit acquérir pour être en orbite basse (à altitude nulle).
4. Il est facile de remarquer que : \[ v=\frac{d}{T} \] où \(d\) est la distance parcourue par le satellite pendant la durée \(T\). Or \(T\) définit le temps de parcours de l'orbite donc \(d\) correspond à la longueur de l'orbite, considérée comme un cercle, cela revient à dire que \(d\) est la circonférence de l'orbite du satellite. Ainsi, on en déduit : \[ v=\frac{2\pi a}{T} \] et la question 2 permet d'écrire, \[ \frac{4\pi^2 a^2}{T^2}=\frac{GM_\odot}{a} \] d'où la troisième loi de Kepler écrite dans le système solaire, \[ \boxed{\frac{T^2}{a^3}=\frac{4\pi^2}{GM_\odot}} \]
4.3. Généralités sur les mouvements
Décrire un mouvement est un savoir-faire à acquérir. Dans ce paragraphe, vous aurez accès à différents adjectifs qui vous permettront de décrire un très grand nombre de mouvements.
Définition 11. (Mouvement elliptique)
On appelle mouvement elliptique un mouvement dont la trajectoire est une ellipse.
Remarque : Dans le chapitre consacré à l'étude des corps célestes et de leur mouvement, nous aurons l'occasion de voir les trois lois de Kepler et en particulier la première qui énonce que tout satellite du système solaire a comme trajectoire une ellipse dont l'un des deux foyers est occupé par le Soleil. Ainsi, en toute rigueur, le mouvement des planètes dans le système solaire est un mouvement elliptique.
Figure 6. - Exemple de trajectoire elliptique avec deux foyers \(F\) et \(F'\)
Définition 12. (Mouvement cycloïdal)
On appelle mouvement cycloïdal un mouvement obtenu par un point fixé à un cercle qui est à la fois en translation et en rotation.

Figure 7. - Exemple de trajectoire cycloïdale
Point méthode
Soit \(M\) un point matériel et on note \(v\) et \(a\) respectivement sa vitesse et son accélération.
- Si \(v\) est une constante au cours du temps, on dit que le mouvement de \(M\) est uniforme. Il en suit que \(a\) est nulle, le mobile \(M\) ne ressent alors aucune accélération.
- Si \(a\) est une constante positive au cours du temps, le mouvement est dit uniformément accéléré.
- Si \(a\) est une constante négative au cours du temps, le mouvement est dit uniformément ralenti.
- Si la vitesse croît au cours du temps alors l'accélération ressentie est positive dans le sens du mouvement.
- Si la vitesse décroît au cours du temps alors l'accélération ressentie est négative dans le sens du mouvement.