Terminale : Mathématiques : Géométrie dans le plan
Dans toute la suite, on se place dans un repère orthonormé \(\left(O,\vec{i},\vec{j}\right)\) définissant alors un plan \(\mathcal{P}\).
📚 Table des matières
1. Premières définitions
Soient \(A\) et \(B\) deux points du plan \(\mathcal{P}\) de coordonnées respectivement \(\begin{pmatrix} x_A \\ y_A \end{pmatrix}\) et \(\begin{pmatrix} x_B \\ y_B \end{pmatrix}\).
Définition 1.
La quantité \(\overrightarrow{AB}\) est appelée vecteur, elle est contenue dans le plan \(\mathcal{P}\) et :
Définition 2.
La quantité \(\lVert \overrightarrow{AB} \rVert\), appelée norme du vecteur \(\overrightarrow{AB}\), est un réel positif et :
Remarque. Pour la culture, cette norme est appelée norme canonique sur \(\mathbb{R}^2\). C'est la norme la plus naturelle qui permet de définir la notion de distance usuelle dans le plan.
Proposition 1.
La longueur du segment \([AB]\) est égale à la norme du vecteur \(\overrightarrow{AB}\).
Définition 3.
Le milieu du segment \([AB]\) notée \(I\) a pour coordonnées :
Exercice 1.
Soient \(A\) et \(B\) deux points du plan \(\mathcal{P}\) de coordonnées respectivement \(\begin{pmatrix} \sqrt{2} \\ \sqrt{2} \end{pmatrix}\) et \(\begin{pmatrix} 1 \\ -1 \end{pmatrix}\).
1. Calculer la longueur du segment \([AB]\).
2. Calculer le milieu du segment \([AB]\).
Définition 4.
On appelle vecteur nul, le vecteur \(\vec{0}\), tel que pour tout vecteur \(\vec{u}\) de \(\mathcal{P}\) :
2. Opérations sur les vecteurs
Soit \(C\) et \(D\) deux autres points du plan \(\mathcal{P}\) de coordonnées respectivement \(\begin{pmatrix} x_C \\ y_C \end{pmatrix}\) et \(\begin{pmatrix} x_D \\ y_D \end{pmatrix}\).
2.1. La somme de vecteurs
Définition 5.
La somme notée \(+\) est définie sur le plan \(\mathcal{P}\) de la manière suivante :
Proposition 2. La relation de Chasles
Tout vecteur du plan \(\mathcal{P}\) peut être décomposé comme une somme faisant intervenir un point intermédiaire.
Preuve
Preuve. Le vecteur \(\overrightarrow{AB}\) a pour coordonnées \(\begin{pmatrix} x_B-x_A \\ y_B-y_A \end{pmatrix}\), le vecteur \(\overrightarrow{AC}\) a pour coordonnées \(\begin{pmatrix} x_C-x_A \\ y_C-y_A \end{pmatrix}\) et le vecteur \(\overrightarrow{CB}\) a pour coordonnées \(\begin{pmatrix} x_B-x_C \\ y_B-y_C \end{pmatrix}\). Il suffit de calculer la somme \(\overrightarrow{AC}+\overrightarrow{CB}\) :
\[ \overrightarrow{AC}+\overrightarrow{CB}=\begin{pmatrix} x_C-x_A+x_B-x_C \\ y_C-y_A+y_B-y_C \end{pmatrix}=\begin{pmatrix} -x_A+x_B \\ -y_A+y_B \end{pmatrix}=\begin{pmatrix} x_B-x_A \\ y_B-y_A \end{pmatrix}=\overrightarrow{AB} \]Cela conclut la preuve.
Définition 6.
On définit l'inverse du vecteur \(\overrightarrow{AB}\) par rapport à la somme \(+\) comme son opposé noté \(-\overrightarrow{AB}\) :
Ainsi, grâce à la définition 6, on peut définir l'opération différence notée \(-\). Il suffit de voir que :
\[ \overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AB}+\left(-\overrightarrow{CD}\right) \]Remarque. On vient là de définir des opérations élémentaires qu'on utilisait déjà dans l'ensemble des réels notée \(\mathbb{R}\). Il manque cependant le fameux produit, ou du moins son équivalent pour les vecteurs. On va d'abord voir un produit sur les vecteurs qui est à valeurs réelles et un second qui donne comme résultat un autre vecteur.
2.2. Le produit scalaire
Définition 7.
On définit le produit scalaire comme l'opération notée \(\langle.|.\rangle\) définie sur \(\mathcal{P}^2\) autrement dit qui prend en argument deux vecteurs du plan et qui renvoie un réel de la manière suivante :
\[ \begin{align*} \langle.|.\rangle : \quad & \mathcal{P}^2 \to \mathbb{R}\\ & \left(\vec{u},\vec{v}\right) \mapsto\langle \vec{u}|\vec{v}\rangle=\lVert \overrightarrow{u} \rVert\lVert \overrightarrow{v} \rVert \cos\left(\vec{u},\vec{v}\right) \end{align*} \]si \(\vec{u}=\begin{pmatrix} x \\ y \end{pmatrix}\) et \(\vec{v}=\begin{pmatrix} x' \\ y' \end{pmatrix}\) alors le produit scalaire devient :
où \(\cos\left(\vec{u},\vec{v}\right)\) est le cosinus de l'angle le plus petit formé entre les vecteurs \(\vec{u}\) et \(\vec{v}\).
Illustrons le produit scalaire dans un cas donné.

Ici, si l'on connaît les coordonnées des vecteurs \(\vec{u}\) et \(\vec{v}\) alors il suffit d'utiliser la seconde formulation du produit scalaire. Mais ici, on peut récupérer toutes les informations nécessaires à l'application de la première formule ! Il suffit d'écrire :
\[ \langle \vec{u}|\vec{v}\rangle=\lVert \overrightarrow{u} \rVert\lVert \overrightarrow{v} \rVert \cos(\alpha) \]Mais c'est généralement la seconde expression du produit scalaire qu'on utilise en pratique. Il suffit de retenir que ces deux écritures du produit scalaire sont équivalentes ! On peut même le prouver.
Remarque. Une observation remarquable : on peut observer que la norme étudiée à la définition 2 se définit facilement grâce à la seconde formulation de notre produit scalaire de la définition 7. En effet, on peut remarquer :
\[ \lVert \overrightarrow{AB} \rVert= \sqrt{\langle\overrightarrow{AB}|\overrightarrow{AB}\rangle} \]Toute norme définie grâce à un produit scalaire est alors appelée norme euclidienne. La norme \(\lVert . \rVert\) de notre définition 2 définie sur le plan \(\mathcal{P}\) est donc une norme euclidienne.
Proposition 3. Les identités de polarisation
Soient \(\vec{u}\) et \(\vec{v}\) deux vecteurs du plan \(\mathcal{P}\) alors :
La preuve est admise car hors programme mais ces formules devraient rappeler au lecteur les identités remarquables qu'il connaît depuis le collège !
Proposition 4. L'identité du parallélogramme
Soient \(\vec{u}\) et \(\vec{v}\) deux vecteurs du plan \(\mathcal{P}\) alors :
Preuve. Il suffit d'additionner les égalités \(\clubsuit\) et \(\spadesuit\) pour obtenir le résultat voulu \(\triangle\).
Remarque. Vigilance pour le lecteur averti : Les identités des propositions 3 et 4 sont vraies pour notre norme (définition 2) mais vous verrez plus tard dans vos études, que ces égalités ne sont pas vérifiées par toutes les normes ! Pour l'observer, on devra définir rigoureusement ce que c'est que la norme mais là, on dépasse le cadre du programme... Mais dans ce cas, tout va bien !
Remarque. Il se peut que dans les autres cours, vous voyez \(\cdot\) au lieu de \(\langle .|.\rangle\), c'est la même chose à une notation près !
Maintenant, nous allons définir un nouveau produit semblable à celui sur \(\mathbb{R}\).
2.3. Le produit vectoriel - HORS PROGRAMME
Avant de définir ce produit, il nous faut définir la notion de vecteur normal à un plan et ici, chercher à exprimer le vecteur normal noté \(\vec{n}\) de notre plan \(\mathcal{P}\).
Définition 8.
Tout plan peut être modélisé par une équation qu'on appelle équation cartésienne du plan. Ainsi, il existe \(a,b,c\) et \(d\) quatre réels tels que l'équation cartésienne du plan \(\mathcal{P}\) s'écrit :
Ici, nous proposons un premier résultat de la géométrie repérée dans l'espace. En effet, on met en équation grâce à des variables la position du plan dans l'espace. Cela permet ainsi de savoir si un point de l'espace \(M\) de coordonnées \(\begin{pmatrix} x_M \\ y_M \\ z_M \end{pmatrix}\) est dans le plan \(\mathcal{P}\). En effet, il suffit de voir :
\[ M\in\mathcal{P}\quad\iff\quad ax_M+by_M+cz_M+d=0 \]Définition 9.
On définit un vecteur normal \(\vec{n}\) comme le vecteur orthogonal (équivalent à être perpendiculaire en géométrie) au plan \(\mathcal{P}\) d'équation cartésienne \(ax+by+cz+d=0\) défini par :
Désormais, on note \(\vec{n}\) un vecteur normal à notre plan \(\mathcal{P}\). Attention, il n'est pas unique ! On admettra pour la suite qu'à partir du plan \(\mathcal{P}\) et de son vecteur normal \(\vec{n}\), on peut construire un espace noté \(\mathcal{E}\).
Définition 10.
On définit le produit vectoriel comme l'opération notée \(\land\) définie sur \(\mathcal{E}^2\) autrement dit qui prend en argument deux vecteurs du plan et qui renvoie un autre vecteur de la manière suivante :
\[ \begin{align*} \land : \quad & \mathcal{E}^2 \to \mathcal{E}\\ & \left(\vec{u},\vec{v}\right) \mapsto \vec{u}\land\vec{v}=\lVert \overrightarrow{u} \rVert\lVert \overrightarrow{v} \rVert \sin\left(\vec{u},\vec{v}\right).\vec{n} \end{align*} \]si \(\vec{u}=\begin{pmatrix} x \\ y \\ z \end{pmatrix}\) et \(\vec{v}=\begin{pmatrix} x' \\ y' \\ z' \end{pmatrix}\) alors le produit vectoriel devient :
où \(\sin\left(\vec{u},\vec{v}\right)\) est le sinus de l'angle le plus petit formé entre les vecteurs \(\vec{u}\) et \(\vec{v}\).
Remarque. La difficulté de calculer un produit vectoriel contrairement à un produit scalaire est qu'il est impératif de connaître un vecteur normal orthogonal au plan contenant \(\vec{u}\) et \(\vec{v}\). Il faudra compléter cette sous-section à l'aide des outils qui seront développés dans le chapitre sur la géométrie repérée dans l'espace.
2.4. Le déterminant
Ici, on revient à l'étude d'un outil vu dès la seconde, celui de déterminant. Initialement, en se donnant deux vecteurs \(\vec{u}\) et \(\vec{v}\) de \(\mathcal{P}\), on peut construire leur somme \(\vec{u}+\vec{v}\). On peut donc construire un parallélogramme \(ABCD\) :
.png)
Nous allons définir un outil qui permet de calculer l'aire de ce parallélogramme.
Définition 11.
On définit le déterminant comme l'opération notée \(\det\) définie sur \(\mathcal{P}^2\) autrement dit qui prend en argument deux vecteurs du plan et qui renvoie un réel de la manière suivante :
\[ \begin{align*} \det : \quad & \mathcal{P}^2 \to \mathbb{R}\\ & \left(\vec{u},\vec{v}\right) \mapsto \det\left(\vec{u},\vec{v}\right) \end{align*} \]si \(\vec{u}=\begin{pmatrix} x \\ y \end{pmatrix}\) et \(\vec{v}=\begin{pmatrix} x' \\ y' \end{pmatrix}\) alors le déterminant devient :
Ainsi, l'aire de notre parallélogramme \(ABCD\) est égale à \(\det\left(\vec{u},\vec{v}\right)\).
3. Propriétés sur les vecteurs
3.1. Colinéarité
Définition 12.
Deux vecteurs sont dits colinéaires lorsque les droites qui les contiennent sont parallèles.
Proposition 5.
Deux vecteurs \(\vec{u}\) et \(\vec{v}\) sont dits colinéaires si et seulement si il existe un réel non nul \(k\) tel que :
La preuve est immédiate, c'est juste la formalisation de la définition 12 avec des outils mathématiques.
Remarque. Deux vecteurs du plan \(\mathcal{P}\) non colinéaires sont dits indépendants.
Proposition 6.
Soient \(\vec{u}\) et \(\vec{v}\) deux vecteurs du plan \(\mathcal{P}\). Les propositions suivantes sont équivalentes :
1. (i) \(\vec{u}\) et \(\vec{v}\) sont colinéaires,
2. (ii) \(|\langle\vec{u}|\vec{v}\rangle|=\lVert \overrightarrow{u} \rVert\lVert \overrightarrow{v} \rVert\),
3. (iii) \(\vec{u}\land\vec{v}=\vec{0}\),
4. (iv) \(\det\left(\vec{u},\vec{v}\right)=0\).
Preuve
Preuve. Nous supposerons que les vecteurs \(\vec{u}\) et \(\vec{v}\) sont non nuls. Cette démonstration est hors programme.
\((i)\Longrightarrow (ii)\) : Si \(\vec{u}\) et \(\vec{v}\) sont colinéaires, alors d'après la définition 12, il en suit que l'angle formé entre ces deux vecteurs est nul ou vaut \(\pi\) or \(\cos(0)=1\) et \(\cos(\pi)=-1\). Ainsi : \(|\langle\vec{u}|\vec{v}\rangle|=\lVert \overrightarrow{u} \rVert\lVert \overrightarrow{v} \rVert\).
\((ii)\Longrightarrow(iii)\) : Si \(|\langle\vec{u}|\vec{v}\rangle|=\lVert \overrightarrow{u} \rVert\lVert \overrightarrow{v} \rVert\), alors l'angle formé entre les vecteurs \(\vec{u}\) et \(\vec{v}\) est soit nul ou vaut \(\pi\). Or \(\sin(0)=\sin(\pi)=0\) donc \(\vec{u}\land\vec{v}=\vec{0}\).
\((iii)\Longrightarrow(iv)\) : Si \(\vec{u}\land\vec{v}=\vec{0}\) alors c'est équivalent à dire que l'angle formé entre les vecteurs \(\vec{u}\) et \(\vec{v}\) vaut \(0\) ou \(\pi\), géométriquement, les droites contenant ces vecteurs sont parallèles. Il en suit que la quadrilatère engendrée par les deux vecteurs est réduit à un segment donc d'aire nulle. D'où, \(\det\left(\vec{u},\vec{v}\right)=0\).
\((iv)\Longrightarrow(i)\) Si l'on revoit notre déterminant comme la mesure d'une aire, la seule figure qui a une aire nulle dans le plan correspond à un segment car \(\det\left(\vec{u},\vec{v}\right)=0\). Il en résulte que nécessairement (on le voit facilement avec un dessin) que les vecteurs \(\vec{u}\) et \(\vec{v}\) sont sur la même droite. D'après la définition 12, \(\vec{u}\) et \(\vec{v}\) sont colinéaires.
Cela conclut la preuve. Les propositions sont toutes équivalentes.
3.2. Orthogonalité
Définition 13.
Deux vecteurs sont dits orthogonaux lorsque les droites qui les contiennent sont perpendiculaires entre-elles.
Proposition 7.
Soient \(\vec{u}\) et \(\vec{v}\) deux vecteurs du plan \(\mathcal{P}\). Les propositions suivantes sont équivalentes :
1. (i) \(\vec{u}\) et \(\vec{v}\) sont orthogonaux,
2. (ii) \(\langle\vec{u}|\vec{v}\rangle=0\),
3. (iii) \(|\vec{u}\land\vec{v}|=\lVert \overrightarrow{u} \rVert\lVert \overrightarrow{v} \rVert.\vec{n}\).
Preuve
La preuve est admise car elle nécessite des arguments vus dans le chapitre de géométrie repérée dans l'espace.
3.3. Vecteur unitaire
Définition 14.
On dit que le vecteur \(\vec{u}\) est unitaire ou normé lorsque sa norme \(\lVert \overrightarrow{u} \rVert\) est égal à 1.
Remarque. Ici, on peut alors traduire ensemble le terme "orthonormé" défini au début du cours : nos vecteurs \(\vec{i}\) et \(\vec{j}\) sont orthonormés, ce qui signifie qu'ils sont orthogonaux \textbf{ET} normés d'où, \(\langle\vec{u}|\vec{v}\rangle=0\) et \(\lVert \overrightarrow{u} \rVert=\lVert \overrightarrow{u} \rVert=1\).
Maintenant que nous avons vu toutes les opérations qu'on peut définir sur les vecteurs dans un plan (et même dans l'espace), nous pouvons voir les théorèmes à connaître en pratique : théorème de Pythagore, théorème de Thalès, théorème d'Al-Kashi et la loi des sinus.
4. Les grands résultats de géométrie dans le plan
Théorème 1. Théorème d'Al-Kashi
Dans tout triangle, les égalités suivantes seront toujours vraies :
.png)
Preuve
Preuve. Il suffit de remarquer que pour montrer la première égalité, \(\vec{a}=\vec{b}+\vec{c}\) puis d'évaluer avec la norme cette égalité et élever le tout au carré et utiliser la première identité de polarisation \(\clubsuit\) où \(||\vec{a}||=a\). On faisant la même chose deux autres fois, on prouve les deux autres égalités. C'est gratuit !
Théorème 2. Théorème de Pythagore
Dans tout triangle rectangle, l'égalité suivante est toujours vraie :
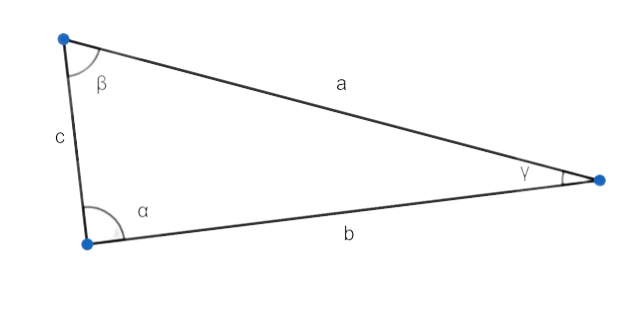
avec \(\alpha=90^\circ\).
Preuve
Preuve. C'est une conséquence du théorème d'Al-Kashi, en effet : en prenant dans le théorème d'Al-Kashi, \(\alpha=90^\circ\) alors, en en déduit l'égalité voulue car \(\cos(90^\circ)=\cos\left(\frac{\pi}{2}\right)=0\).
Théorème 3. Théorème de Thalès
Dans la configuration suivante, nous pouvons dire :
.png)
avec les droites contenant \([BE]\) et \([CD]\) parallèles entre elles.
Preuve
Ce théorème est admis.
Théorème 4. Loi des sinus
Dans tout triangle, l'égalité suivante est toujours vraie :
.png)
Remarque. En général, ce résultat n'est pas vraiment à retenir pour l'instant mais il est utile dans pleins de domaines de la physique comme l'étude des miroirs sphériques en optique géométrique. Il peut quand même être bon de savoir qu'un tel résultat existe !
Proposition 8. Somme des angles dans un triangle
Dans un triangle du plan, la somme des angles est égale à \(180^\circ\).
Preuve
Nous ne démontrerons pas ce résultat car il n'est pas dans le programme. En revanche, vous pouvez toujours faire l'exercice qui suit qui démontre un cas plus général que la proposition 8.
Exercice.
On appelle polygone toute figure fermée dans le plan dont les contours sont des segments. Parmi les polygones, il existe une classe de polygones qu'on appelle polygone convexe. Les polygones convexes sont des polygones qui en plus vérifient la propriété suivante : lorsqu'on prend \(A\) et \(B\) deux points dans le polygone alors le segment \([AB]\) reste dans le polygone. On admettra la proposition 8.
Montrer par récurrence sur \(n\ge3\) que la somme des angles d'un polygone convexe à \(n\) côtés est égale à \((n-2)\pi\).
5. Représentation paramétrique d'une droite
Définition 15.
Toute droite dans le plan admet comme équation :
où \(a\) et \(b\) sont deux réels déterminés.
Proposition 9. Représentation paramétrique d'une droite
Toute droite dans le plan admet un système paramétrique défini comme :
où \(A\) est un point de la droite et \(\vec{u}=\begin{pmatrix} a \\ b \end{pmatrix}\) est un vecteur sur la droite.
Preuve
La preuve sera faite dans le chapitre de géométrie repérée dans l'espace.
Remarque. La proposition 9 permettra d'étudier si un plan croise une droite, ce qui est toujours le cas lorsque la droite n'est pas parallèle au plan, et en quel point (ces coordonnées ?). Il suffit d'observer que les points d'une droite vérifie son système paramétrique associé.