Terminale : Comportement géométrique de la lumière
L'objectif de ce cours est d'introduire les lois, utilisées en optique géométrique, qui permettent de prédire la trajectoire empruntée par la lumière dans un milieu (vide ou milieu matériel).
📚 Table des matières
1. Définitions fondamentales
Certaines des notions introduites ici ont déjà été expliquées dans le cours sur l'effet Doppler (section 3 du chapitre). Nous vous recommandons vivement d'aller le regarder pour comprendre un exemple de leur application.
Définition 1. (L'indice optique)
On appelle indice optique d'un milieu, la grandeur notée \(n\) définie comme suit :
Postulat 1. (Vitesse de la lumière)
La vitesse de la lumière est la même dans tous les référentiels. La lumière impose comme étant la limite physique des vitesses, sa vitesse dans le vide. On la note \(c\) et elle vaut environ \(3.10^8\) m.s⁻¹.
Ce postulat permet toujours d'écrire : \(v \le c\) avec \(v\) la vitesse de la lumière dans n'importe quel milieu. Ainsi, on en déduit que tout indice optique est minoré par 1, c'est-à-dire, \(n \ge 1\).
Définition 2. (Dioptre)
On appelle dioptre, la surface en trois dimensions ou encore la frontière en deux dimensions qui sépare deux milieux d'indices optiques différents.
2. Les lois de la réflexion
On considère la situation suivante : un rayon incident arrive en un point du dioptre, qu'on appelle point d'incidence qu'on notera \(I\). Le rayon incident est dans un milieu d'indice optique \(n_1\) et après la dioptre, le milieu est d'indice optique \(n_2\).
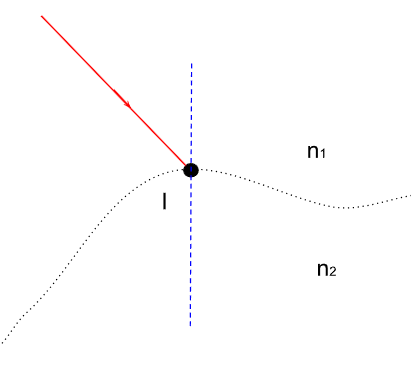
Figure 1. Mise en situation du problème étudié
La droite bleue en pointillé correspond à la normal locale en \(I\). C'est la droite qui est perpendiculaire à la portion du dioptre centrée en \(I\).
Lorsque le rayon incident arrive en \(I\), il donne naissance à deux rayons : le rayon réfléchi et le rayon réfracté. Nous nous intéressons dans cette section au rayon réfléchi. On a alors pour l'instant :
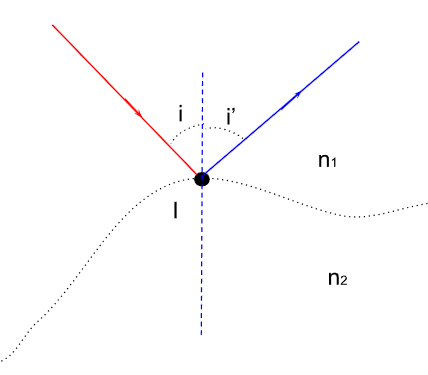
Figure 2. Apparition d'un rayon réfléchi
Définition 3. (Le plan d'incidence)
On appelle plan d'incidence, le plan engendré par le rayon incident et la normal au point d'incidence. En d'autres termes, c'est la plan qui contient à la fois le rayon incident et la normale.
Proposition 1. (Les lois de la réflexion)
Les lois de la réflexion postule que :
1 - Le rayon réfléchi appartient au plan d'incidence.
2 - L'angle formé par le rayon réfléchi avec la normale appelé angle réfléchi est le même que celui formé par le rayon incident avec la normale aussi appelé angle incident.
La première loi permet de placer le problème de réflexion en deux dimensions.
La seconde loi se traduit à l'aide de la figure 2 comme suit : \[ \boxed{i=i'} \]
3. Les lois de la réfraction
Comme dit précédemment, lorsque le rayon incident arrive en un point du dioptre, il donne naissance à deux rayons, le rayon réfléchi et réfracté. On étudie ici les caractéristiques de ce rayon réfracté qu'on représente comme suit :
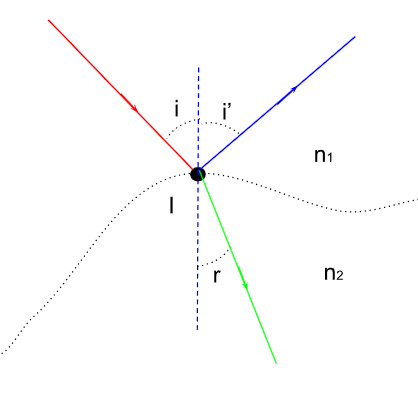
Figure 3. Apparition d'un rayon réfracté
Proposition 2. (Les lois de la réfraction)
Les lois de la réfraction postule que :
1 - Le rayon réfracté appartient au plan d'incidence.
2 - L'angle formé par le rayon réfracté avec la normale appelé angle réfracté obéit à l'égalité suivante :
La première loi permet de justifier que le problème de réfraction est en deux dimensions. De plus, ce plan est le même que celui où on étudie la réflexion.
Enfin, la seconde loi est aussi appelée loi de Snell-Descartes.
Dans la fiche d'exercice, nous nous intéresserons à un exercice classique qui portera sur l'étude de la réfraction à travers un prisme transparent.
Définition 4. (Réfraction limite)
On appelle réfraction limite, le phénomène où il est encore possible d'apercevoir un rayon réfracté.
Le phénomène de réfraction limite correspond un angle réfracté de \(90^\circ\) aussi égal à \(\frac{\pi}{2}\). C'est sa condition d'existence.
Définition 5. (Réflexion totale)
On appelle réflexion totale, le phénomène durant lequel toute l'énergie concentrée dans le rayon incident est transmis intégralement au rayon réfléchi.
Le phénomène de réflexion totale implique la disparition du rayon réfracté. Il n'y alors que le rayon incident et le rayon réfléchi.
Le phénomène de réflexion totale est couramment utilisé dans l'exploitation de dispositifs comme la fibre optique. La fibre optique est une sorte de fil dur constitué de deux parties, une gaine qui la recouvre et un cœur transparent qui laisse passer la lumière qui la traverse. Pour éviter d'avoir des pertes d'énergie (diffusion de la lumière au cours de son trajet), il faut que l'énergie entrante soit égale à l'énergie sortante. Cela est possible quand l'énergie du rayon incident est intégralement contenue dans le rayon réfléchi donc, on cherche à avoir une réflexion totale.
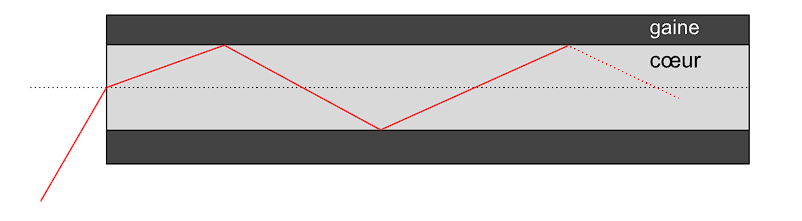
Figure 4. Modèle simplifié de fibre optique, en rouge le parcours de la lumière
Définition 6. (Milieu plus ou moins réfringent)
On dit d'un milieu qu'il est plus réfringent d'un autre lorsque son indice optique est supérieur à celui de l'autre milieu. Lorsque ce dernier est inférieur à l'indice optique de l'autre milieu, on parle de milieu moins réfringent.
Proposition 3. (Première condition d'existence de la réflexion totale)
Le phénomène de réflexion totale peut apparaître lorsque le rayon incident qui se propage dans un milieu d'indice optique \(n_1\) rencontre le dioptre d'un milieu moins réfringent d'indice optique \(n_2\). En d'autres termes, cela se traduit par :
Proposition 4. (Seconde condition d'existence de la réflexion totale)
Si la première condition d'existence de la réflexion totale est vérifiée, alors il existe un angle appelé angle limite noté \(i_l\) tel que si l'angle incidence est supérieur à ce dernier, alors on observera toujours le phénomène de réflexion totale. On doit vérifier alors que :
Dans le cas où \(i=i_l\), on retrouve le phénomène de réfraction limite.
Proposition 5. (Angle limite de réflexion totale)
Dans le cas où les deux conditions d'existence de la réflexion totale sont vérifiées alors avec les notations précédentes, l'angle limite de réflexion totale noté \(i_l\) s'écrit :
Preuve
On utilise les notations de la figure 3. Comme on étudie un phénomène de réfraction, on utilise les lois de la réfraction et en particulier celle de Snell-Descartes qui postule que : \[ n_1\sin(i)=n_2\sin(r) \] Or en réfraction limite, l'angle réfracté vaut \(\frac{\pi}{2}\) d'où : \[ n_1\sin(i)=n_2 \] D'autre part, on sait qu'à la réfraction limite, l'angle limite d'incidence vérifie l'égalité suivante : \[ i=i_l \] On en déduit alors la relation suivante : \[ n_1\sin(i_l)=n_2 \iff \boxed{i_l=\arcsin\left(\frac{n_2}{n_1}\right)} \]
Remarque : Si l'on adopte une démarche mathématique, on comprend mieux les deux conditions d'existence de la réflexion totale. En effet, d'abord si \(n_1>n_2\), c'est pour que l'angle limite soit bien défini car la fonction \(\arcsin\) est défini sur \([-1;1]\) et dérivable sur \(]-1;1[\). Enfin, si l'on a \(i>i_l\), c'est pour éviter d'avoir un angle réfracté \(r>90^\circ\). Logique étant donné que dans ce cas, on a plus d'angle réfracté au sens propre car \(r\in[0;90^\circ]\).
Dans la fiche d'exercices, nous verrons des applications du phénomène de réflexion totale lorsqu'on étudiera le miroir parfait ou encore la fibre optique avec un modèle simplifié.