Terminale : Les interférences
Ce chapitre fait suite au chapitre sur la diffraction. Dans le cours sur la diffraction, nous avions obtenu une figure à l'écran appelée figure de diffraction. Dans ce cours, nous allons voir qu'il est possible d'obtenir des configurations similaires à l'écran lorsqu'on considère deux ondes incidentes et non plus qu'une. On appellera alors ces figures, figures d'interférences.
📚 Table des matières
1. Superposition de deux ondes
Dans le cadre du programme, nous ne considérerons que des ondes lumineuses pour se simplifier la modélisation du problème. Pour mieux introduire les notions développées ici, nous allons d'abord mettre en oeuvre un montage expérimental qui permet de tenir compte du phénomène de superposition.
On considère une source ponctuelle \(S\) qui émet des rayons lumineux dans toutes les directions (on parle de source lumineuse ponctuelle et sphérique). On place à une distance arbitraire de \(S\), un dispositif de trous appelé fentes d'Young. Ensuite, on place à une distance \(D\) des fentes, un écran pour récupérer la figure lumineuse obtenue en sortie. Il conviendra de réaliser ce dispositif suivant un même axe horizontal.
On considère deux rayons lumineux provenant de \(S\), notées \((1)\) et \((2)\) tels que \((1)\) passe par la première fente et \((2)\) par la seconde. Seuls, ces rayons sont diffractés au niveau de la fente comme vu dans le chapitre sur la diffraction. Nous allons voir que comme ils sont diffractés, changeant de direction de propagation, ils vont se recouvrir et donnés naissance à ce qu'on appelle des interférences : ils interfèrent entre eux.
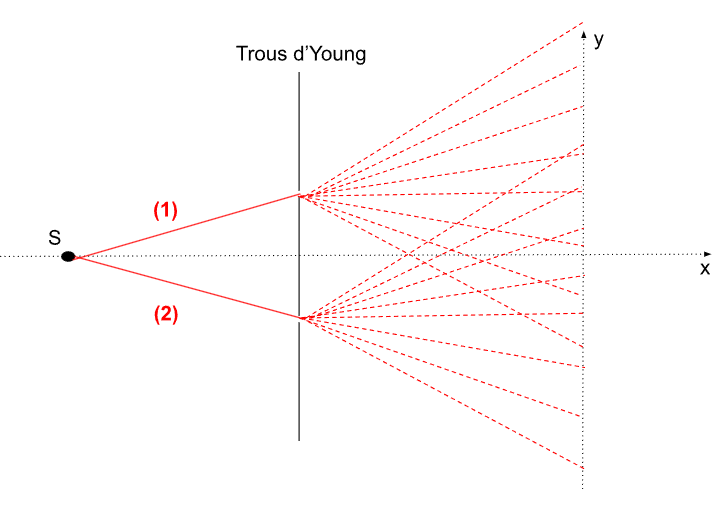
Figure 1. Phénomène observé dans l'expérience des fentes d'Young
Ce qu'on l'en obtient dans la figure 1, c'est la superposition de deux phénomènes de diffraction en les deux fentes. On observe bien que certains rayons en sortie se superposent avec d'autres. C'est ce qui donne naissance au phénomène d'interférences. On définit alors la notion d'interférences.
Définition 1. (Phénomène d'interférences)
Le phénomène d'interférences résulte d'une superposition d'au moins deux ondes de même longueur d'onde provenant d'une même source.
Pour être plus rigoureux, deux ondes interfèrent, on parle aussi d'ondes synchrones lorsqu'elles ont la même pulsation et que leur déphasage commun est quasi-constant. La pulsation d'une onde, notée \(\omega\), est définie comme suit :
\[ \boxed{\omega=2\pi f} \] avec \(f\) la fréquence de l'onde. Leur déphasage quant à lui est liée au retard entre les deux ondes, il est noté \(\Delta t\) et est définit comme suit : \[ \Delta \varphi = \omega\Delta t \] avec \(\Delta t\) le retard entre les deux ondes et \(\omega\) leur pulsation commune.
Ici, comme les ondes considérées sont de même longueur d'onde alors elles sont la même pulsation car \(\omega\), la pulsation, est liée à la longueur d'onde \(\lambda\) par l'expression : \[ \omega=2\pi\frac{v}{\lambda} \] avec \(v\) la vitesse des deux ondes, supposée égale : milieu isotrope (qui présente les mêmes propriétés dans toutes les directions de l'espace). Enfin, comme elles proviennent de la même source, alors elles ont la même phase et donc leur déphasage est nul, il n'y a pas de retard sur \((1)\) par rapport à \((2)\). Donc, \[ \Delta \varphi=0 \] et c'est ainsi, qu'on en déduit que deux ondes provenant de la même source et de longueur d'onde égale peuvent interférer si elles sont superposer.
2. Notion de différence de marche
Dès à présent, on suppose que le milieu considéré est l'air (ou même le vide, les résultats seront égaux). Cette hypothèse provient de la définition d'indice optique qui a été développée dans le cours sur l'effet Doppler.
De plus, on considère un point \(M\) de coordonnées \((0,y)\) dont on trace les rayons qui se joignent en ce dernier.

Figure 2. Superposition des rayons lumineux incidents en \(M\)
Définition 2. (La différence de marche)
La notion de différence de marche est liée à la différence de chemins parcourue par une même onde. On la note \(\delta\), elle est définie en un point de l'espace noté \(M\) et se détermine par l'expression : \[ \delta(M)=(SM)_2-(SM)_1 \] où \((SM)_1\) est le chemin parcouru par l'onde suivant le rayon \((1)\) pour aller de \(S\) à \(M\) et \((SM)_2\) est le chemin parcouru par l'onde suivant le rayon \((2)\) pour aller de \(S\) à \(M\).
Notons que la notion de différence de marche peut être assimilée à celle de retard mais dans l'espace : si \(\delta(M)>0\) alors le rayon \((2)\) met plus de temps a aller du point \(S\) au point \(M\) que le rayon \((1)\).
La démonstration proposée dans cette section pour déterminer l'expression de \(\delta(M)\) n'est pas à connaître à cause en particulier de la proposition 1 définie après, hors programme au lycée. Il est en revanche impératif de connaître son expression.
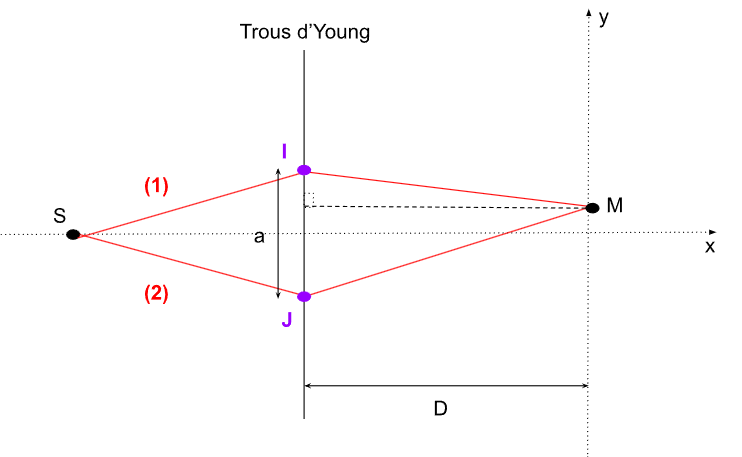
Figure 3. Mise en évidence du problème étudié
On définit \(I\) et \(J\) deux points intermédiaires sur la figure 3. D'abord, remarquons que : \[ (SM)_1=SI+IM \quad \textrm{et} \quad (SM)_2=SJ+JM \]
Remarque : Pour l'instant, nous n'utilisons par le point \(H\), il sera utilisé dans le compléments pour retrouver d'une autre façon l'expression de la différence de marche.
Il est clair par symétrique par rapport à l'axe \(x\) que les distances \(SI\) et \(SJ\) sont égales. On en déduit alors que : \[ \delta(M)=JM-IM \] Le théorème de Pythagore permet d'écrire que : \[ IM=\sqrt{D^2+\left(\frac{a}{2}-y\right)^2}\quad \textrm{et}\quad JM=\sqrt{D^2+\left(\frac{a}{2}+y\right)^2} \] On rappelle que \(y\) désigne l'ordonnée du point \(M\) d'abscisse nulle. On en déduit alors que : \[ \begin{align*} \delta(M)&=\sqrt{D^2+\left(\frac{a}{2}+y\right)^2}-\sqrt{D^2+\left(\frac{a}{2}-y\right)^2}\\ &=D\sqrt{1+\left(\frac{\frac{a}{2}+y}{D}\right)^2}-D\sqrt{1+\left(\frac{\frac{a}{2}-y}{D}\right)^2}\\ &=D\left(\sqrt{1+\left(\frac{\frac{a}{2}+y}{D}\right)^2}-\sqrt{1+\left(\frac{\frac{a}{2}-y}{D}\right)^2}\right) \end{align*} \]
Proposition 1. (Équivalent de \(\sqrt{1+x}\) avec \(|x|\ll 1\) - (HP))
Si \(|x| \ll 1\) alors, il est acceptable d'écrire :
On suppose dorénavant que \(D \gg a\) et \(D \gg y\), donc : \[ \frac{\frac{a}{2}+y}{D} \ll 1 \quad \textrm{et} \quad \frac{\frac{a}{2}-y}{D} \ll 1 \] et il en suit que : \[ \left(\frac{\frac{a}{2}+y}{D}\right)^2 \ll 1 \quad \textrm{et} \quad \left(\frac{\frac{a}{2}-y}{D}\right)^2 \ll 1 \] En reprenant l'expression de \(\delta(M)\), on en déduit que : \[ \begin{align*} \delta(M)&\approx \frac{D}{2}\left(\left(1+\left(\frac{\frac{a}{2}+y}{D}\right)^2\right)-\left(1+\left(\frac{\frac{a}{2}-y}{D}\right)^2\right)\right)\\ &\approx \frac{D}{2}\left(\frac{\frac{a}{2}+y}{D}+\frac{\frac{a}{2}-y}{D}\right)\left(\frac{\frac{a}{2}+y}{D}-\frac{\frac{a}{2}-y}{D}\right)\\ &\approx \frac{D}{2}\times\frac{a}{D}\times\frac{2y}{D}\\ &\approx \frac{ay}{D} \end{align*} \]
Proposition 2. (Expression de la différence de marche)
Si \(M\) a pour coordonnées \((0,y)\), \(D\) la distance entre les trous d'Young et l'écran, \(a\) le pas des trous d'Young (distance entre les deux trous) avec \(D \gg y\) et \(D \gg a\) alors la différence de marche dans le dispositif des trous d'Young a pour expression :
En généralisant avec \(M\) un point de coordonnées \((x,y)\) et un milieu d'indice optique \(n\) supposé constant (cours sur l'effet Doppler) alors, l'expression de \(\delta(M)\) devient : \[ \boxed{\delta(M)=\frac{nay}{D+x}} \]
Maintenant qu'on a l'expression de la différence de marche, on peut déterminer une condition sur \(\delta(M)\) pour qu'en \(M\), les interférences soient constructives (apparition d'une bande verte lumineuse) ou destructives (absence de bande lumineuse). C'est une reformulation des conditions d'interférence posées à la définition 1. Enfin, on pourra déterminer la notion d'interfrange.
3. Les conditions d'interférence
Définition 3. (Les interférences constructives)
On dit que des interférences sont constructives lorsqu'elles correspondant à des régions de l'espace dans lesquels l'amplitude de l'onde résultante est maximale.
Dans le cas de la lumière, cela correspond au centre des bandes lumineuses observées à l'écran dans l'expérience des trous d'Young.
Il est clair que cela correspond au fait que les deux ondes incidentes doivent aussi atteindre leur maximum d'amplitude pour que leur somme, l'onde résultante, atteigne son maximum d'amplitude. Si l'on revenait à la notion de déphasage, cela correspond à un déphasage nul au point où le maximum est atteint.
Essayons de retrouver le critère sur \(\delta(M)\) pour que les interférences au point \(M\) soient constructives. En \(M\), si on veut des interférences constructives, les deux ondes \((1)\) et \((2)\) doivent être maximales en \(M\). Comme ce sont les mêmes ondes et qu'elles sont considérées périodiques dans le temps et dans l'espace alors si le retard de longueur entre \((1)\) et \((2)\) en \(M\) est un multiple de la période spatiale notée \(\lambda\) alors cela correspond au fait que les deux ondes sont maximales en \(M\). On a alors que :
Proposition 3. (Conditions pour obtenir des interférences constructives)
Pour que les interférences soient constructives en un point \(M\) alors la différence de marche en \(M\) notée \(\delta(M)\) est un multiple de la longueur d'onde des ondes considérées :
Une preuve correspondrait à l'explication précédente. Il est possible de retrouver ce résultat en considérant que la notion de déphasage, en effet si l'on note \(\Delta \varphi(M)\) le déphasage en \(M\) des deux ondes alors : \[ \boxed{\Delta \varphi(M)=\frac{2\pi}{\lambda}\delta(M)} \]
Définition 4. (Les interférences destructives)
On dit que des interférences sont destructives lorsqu'elles correspondant à des régions de l'espace dans lesquels l'amplitude de l'onde résultante est nulle.
Dans le cas de la lumière, cela correspond au centre des bandes sombres observées à l'écran dans l'expérience des trous d'Young.
De la même façon, on en déduit la condition pour obtenir des interférences destructives :
Proposition 4. (Conditions pour obtenir des interférences destructives)
Pour que les interférences soient destructives en un point \(M\) alors la différence de marche en \(M\) notée \(\delta(M)\) est un multiple à un demi près de la longueur d'onde des ondes considérées :
4. Notion d'interfrange
En s'aidant des parties précédentes, on peut définir une distance caractéristiques des figures d'interférences, l'interfrange.
Définition 5. (L'interfrange)
On appelle interfrange, notée \(i\), la distance entre deux raies brillantes ou deux raies sombres.
En effet, la distance entre deux raies brillantes est égale à la distance entre deux raies sombres. Cette distance se mesure en général directement sur une figure d'interférences.
Proposition 5. (Interfrange dans l'expérience des trous d'Young)
Si l'on note \(i\) l'interfrange dans l'expérience des cas d'Young, \(a\) le pas des trous d'Young, \(D\) la distance entre les fentes et l'écran et \(\lambda\) la longueur d'onde des ondes considérées alors,
Preuve
Considérons la distance entre deux franges brillantes. On considère deux raies brillantes successives alors, la \(n-\)ème et la \((n+1)-\)ème. On note \(y_n\) et \(y_{n+1}\) leur ordonnée respective. Alors par définition de l'interfrange, on a : \[ i=y_{n+1}-y_n \] Or ces ordonnées sont données par, dans l'hypothèse des franges brillantes, la proposition 3. En effet, \[ \delta(y=y_n)=n\lambda \quad \textrm{et} \quad \delta(y=y_{n+1})=(n+1)\lambda \] et en utilisant la proposition 2, on a : \[ \frac{ay_n}{D}=n\lambda \quad \textrm{et} \quad \frac{ay_{n+1}}{D}=(n+1)\lambda \] Finalement, on en déduit que : \[ y_n=n\frac{\lambda D}{a} \quad \textrm{et} \quad y_{n+1}=(n+1)\frac{\lambda D}{a} \] On en déduit alors que : \[ \boxed{i=\frac{\lambda D}{a}} \] ce qui achève notre preuve.