Tale Spécialité : Physique : La diffraction
Dans ce chapitre, nous étudions un phénomène d'optique qui prend naissance lorsqu'un rayon lumineux de longueur d'onde \(\lambda\) traverse une fente d'ouverture \(a\) avec \(a\sim\lambda\) en ordre de grandeur : la diffraction.
📚 Table des matières
1. Le phénomène de diffraction
Définition 1. (La diffraction)
La diffraction est un phénomène représentant la propriété d'une onde qui, au passage d'un obstacle, s'étale dans toutes les directions de l'espace. Le phénomène est d'autant plus visible lorsque la taille de l'obstacle diminue.
Proposition 1. (Condition d'existence de la diffraction)
Si l'on note \(a\) la taille de l'obstacle et \(\lambda\) la longueur de l'onde incidente alors la diffraction est visible si et seulement si, en ordre de grandeur, on a :
Nous pouvons voir à quoi correspond en réalité la définition 1 avec la figure suivante :
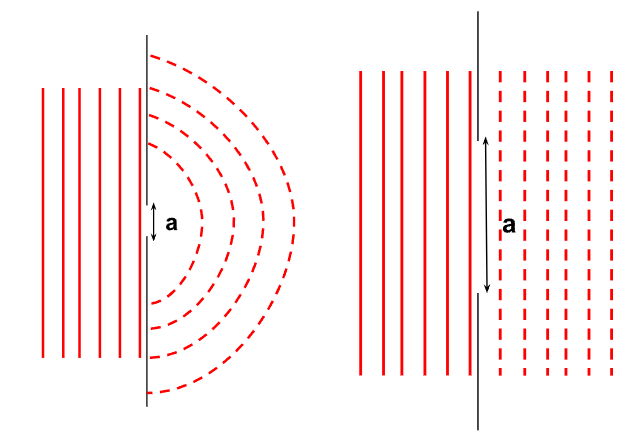
Figure 1. Mise en évidence de la diffraction sous condition d'existence
La représentation de gauche représente le phénomène de diffraction car ici, la longueur d'onde \(\lambda\) de l'onde incidente est du même ordre de grandeur que la taille de la fente \(a\). En revanche, la représentation de droite ne vérifie pas la proposition 1 donc en sortie, après la fente, l'onde garde son état initial.
Exemple. Il est fréquent d'observer ce phénomène lorsqu'on étudie comment se reforment des vagues en mer en entrant dans un port par exemple. Dans certains ports, l'ouverture du port est du même ordre de grandeur que l'onde incidente (succession de vagues), ainsi au départ elles sont verticales et après, elles s'étalent comme dans la première représentation de la figure 1.
Exercice.
Dire, dans les deux cas suivants, si l'onde émise en un point \(A\) de l'espace est correctement entendue en un autre point \(B\) de l'espace.
1. On suppose que \(A\) correspond à un laser qui émet une onde lumineuse de longueur d'onde 530 nm et \(B\) un observateur placé à 1 m de \(A\). On suppose aussi qu'entre \(A\) et \(B\), on place une feuille d'épaisseur 0,1 mm.
2. On considère qu'en \(A\) une personne parle au téléphone et en \(B\) une seconde personne. On suppose qu'entre les deux, il y a un arbre de diamètre 30 cm.
Données : On rappelle que la vitesse de la lumière dans l'air est d'environ 300 000 km.s⁻¹ et celle du son, dans l'air aussi, vaut 300 m.s⁻¹.
2. Le cas d'une onde lumineuse
Dans le cadre du programme, on étudie en particulier le cas des ondes lumineuses. On considère alors un faisceau lumineux modélisé par un rayon géométrique de longueur d'onde \(\lambda\) qui traverse une fente (ouverture) de taille \(a\). On suppose que la condition de la proposition 1 est vérifiée.
On réalise le montage suivant pour voir comment se diffracte la lumière : on place un laser qui émet un faisceau lumineux de couleur vert devant une fente de taille \(a\). Après la fente, on dispose un écran de façon à voir une figure lumineuse.
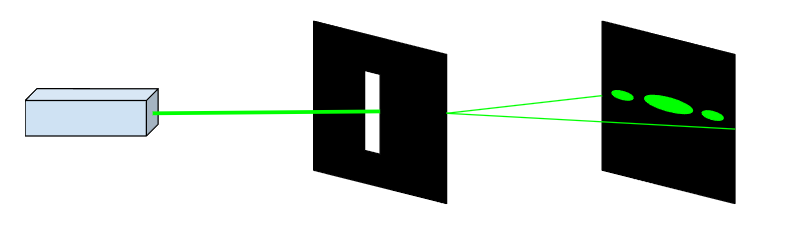
Figure 2. Montage réalisé et résultat obtenu
La figure obtenue sur l'écran est appelée figure de diffraction, elle permet de rendre compte de la déformation de l'onde incidente en sortie de la fente. Elle a changé de direction.

Figure 3. Figure de diffraction obtenue à l'écran
L'objectif de cette partie est de voir s'il ne serait pas possible d'établir des relations entre les grandeur mises en jeu dans ce problème. On introduit alors \(w\) l'écart angulaire entre les deux rayons extrêmes de la figure 2, \(L\) la largeur de la tâche centrale et \(D\) la distance entre l'écran et la fente. Résumons cela dans la figure suivante :
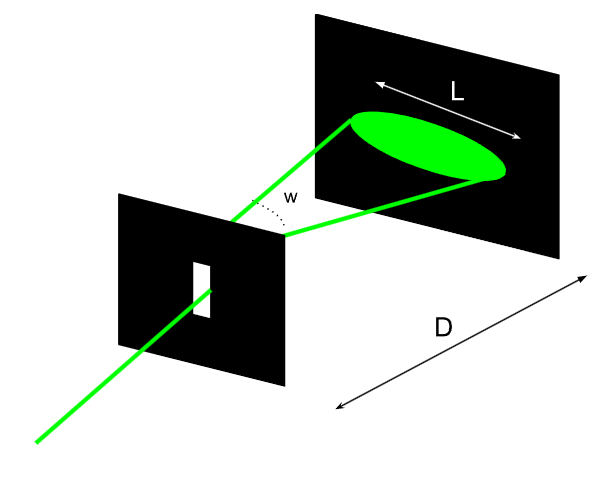
Figure 4. Mise en évidence du problème étudié
Toute la suite constitue un schéma de raisonnement à maîtriser pour le BAC.
Définition 2. (Angle de diffraction)
L'angle de diffraction, noté \(\theta\), est proportionnelle à la l'ouverture de la fente notée \(a\) et à la longueur d'onde de l'onde incidente notée \(\lambda\) : \[ \sin(\theta)=\frac{\lambda}{a} \]
Remarque : Cet angle permet de définir à quel point la diffraction est visible et donc, permet d'exprimer la condition d'existence de la proposition 1. Si la taille de la fente \(a\) augmente, l'angle \(\theta\) tend vers 0 et ainsi, il n'y a pas de changement de direction de l'onde incidente après son passage dans la fente. Si \(a\) diminue, la valeur de \(\frac{\lambda}{a}\) augmente et donc l'angle \(\theta\) aussi. On notera qu'on a fixé la valeur de \(\lambda\) dans l'interprétation précédente.
En s'aidant de la figure 4, on peut aussi définir l'angle de diffraction \(\theta\) par la relation : \[ \theta=\frac{w}{2} \] En utilisant le formulaire trigonométrique, on a : \[ \tan(\theta)=\frac{\frac{L}{2}}{D}=\frac{L}{2D} \] Dans l'approximation des petits angles, il en suit que : \[ \tan(\theta)\approx\theta \] et ainsi, on en déduit que :