La Chute d'Icare : Une prouesse astrophotographique "absolument absurde"
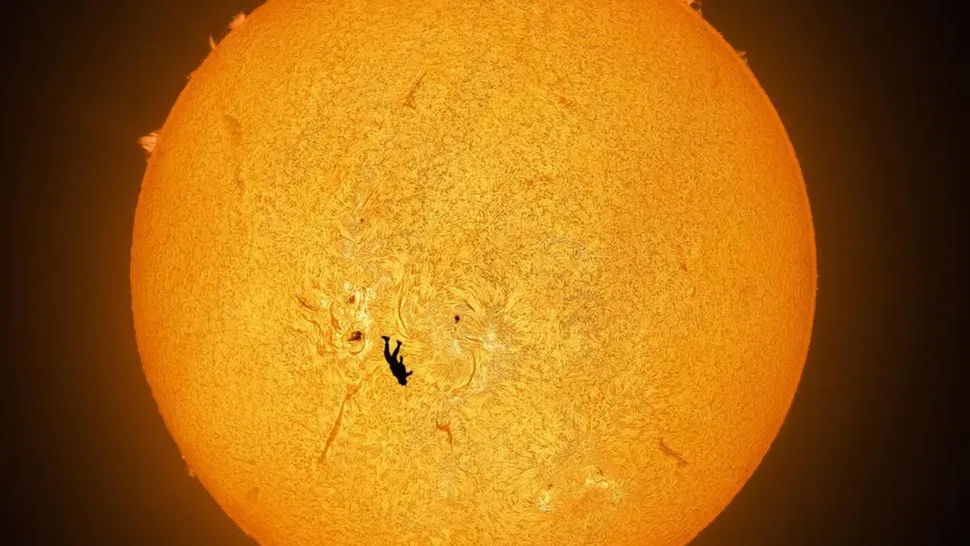
📐 Un défi technique "absolument absurde"
📸 Andrew McCarthy
Astrophotographe célèbre pour ses clichés ultra-détaillés du cosmos. Il a qualifié la planification de ce cliché d'"absolutely preposterous" (absolument absurde) sur la plateforme X, soulignant la complexité d'aligner deux objets en mouvement rapide.
Contrairement à la photographie d'objets célestes dont les trajectoires sont prévisibles grâce aux éphémérides, photographier un parachutiste en chute libre devant le Soleil ajoute une variable chaotique majeure : l'humain et la mécanique de vol atmosphérique.
Pour réussir ce cliché, McCarthy a dû calculer précisément la trajectoire du Soleil et coordonner le saut avec une précision de l'ordre de la seconde. Il ne s'agissait pas simplement de viser le Soleil et d'attendre ; il fallait que le parachutiste traverse un "couloir" invisible dans le ciel, aligné parfaitement avec l'objectif du télescope situé à plusieurs kilomètres de là.
— Andrew McCarthy
Les chiffres de l'exploit
🔬 Analyse Scientifique de l'Alignement
Pour comprendre la difficulté de cette prise de vue, il faut analyser la géométrie de l'alignement. Le défi principal réside dans la taille angulaire apparente des objets et leur vitesse relative.
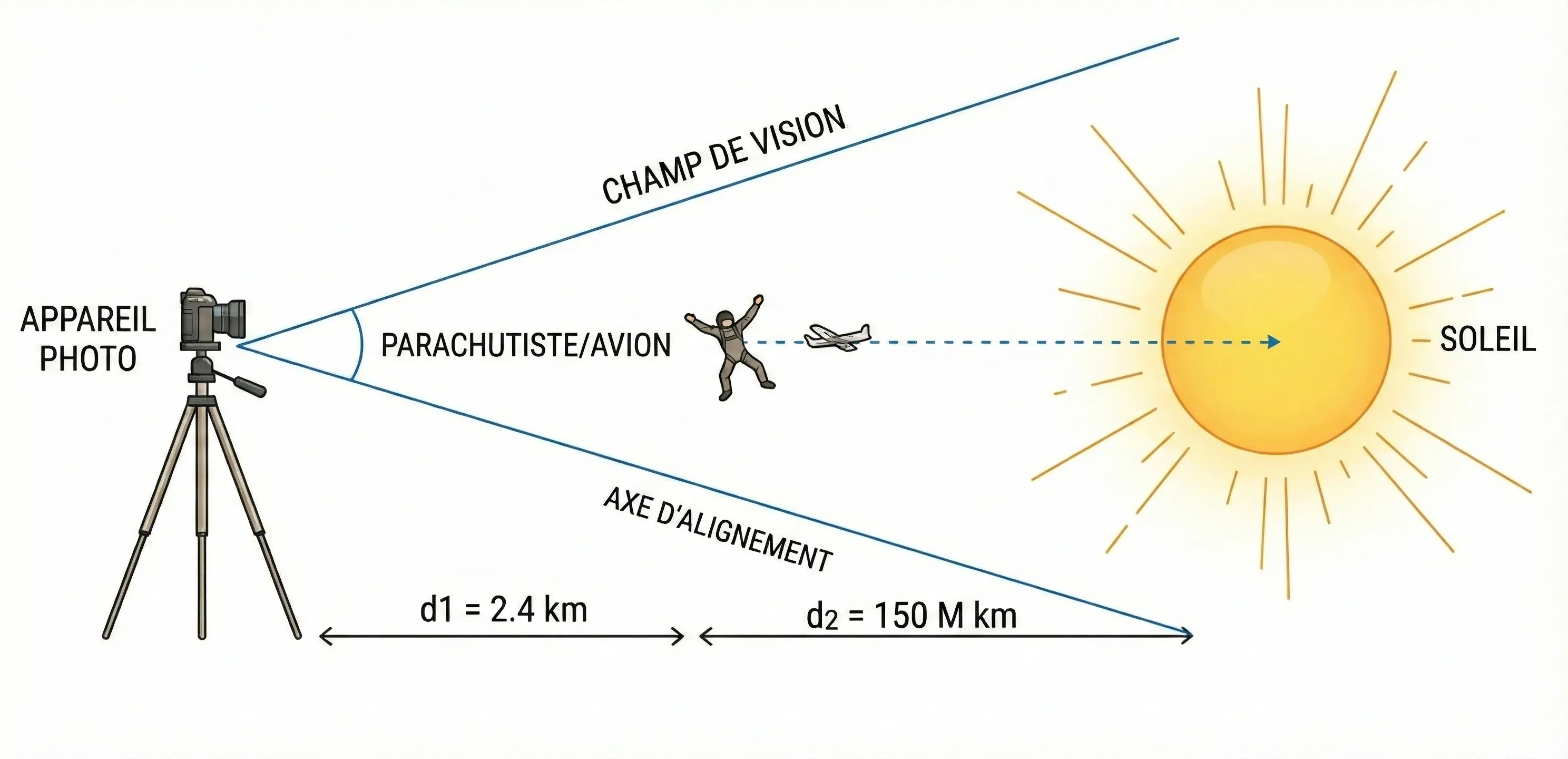
Taille angulaire et Approximation des petits angles
La taille angulaire \(\theta\) d'un objet est l'angle sous lequel il est vu par l'observateur. Trigonométriquement, pour un objet de diamètre \(d\) à une distance \(D\), on a la relation :
Cependant, en astronomie, les angles sont si petits que l'on utilise l'approximation des petits angles. Lorsque \(\theta\) est très petit (en radians), la tangente de l'angle est presque égale à l'angle lui-même : \(\tan(\theta) \approx \theta\).
Pour le parachutiste (\(d \approx 2m\), \(D \approx 2400m\)), le rapport est de \(0,00083\) radians. Converti en degrés (\(\times \frac{180}{\pi}\)), cela donne \(\theta \approx 0,048^\circ\). C'est environ 1/10ème du diamètre apparent du Soleil (\(0,53^\circ\)). Cette précision mathématique montre qu'un décalage de quelques mètres seulement aurait suffi à rater la photo.
Temps de transit
Le parachutiste est en chute libre, accélérant sous l'effet de la gravité avant d'atteindre sa vitesse terminale. À une vitesse estimée de \(v \approx 50 \text{ m/s}\) (environ 180 km/h), le temps de passage \(t\) devant le disque solaire (qui représente une largeur \(L \approx 22m\) à cette distance) est extrêmement bref :
Cela laisse moins d'une demi-seconde pour déclencher l'obturateur au bon moment. McCarthy a probablement utilisé un mode rafale à haute vitesse pour maximiser ses chances de capturer la silhouette au centre du disque.
📷 Le Matériel de l'Extrême
Capturer une telle image demande un équipement bien spécifique, loin des appareils photo standards. Voici une reconstitution probable du "setup" utilisé pour ce type de prouesse :
Télescope Solaire Modifié
Probablement une lunette astronomique équipée d'un filtre de rejet d'énergie pour protéger l'optique de la chaleur intense.
Filtre H-alpha
Un étalon Fabry-Pérot qui isole la raie de l'hydrogène (656.28 nm) pour révéler la chromosphère.
Caméra Monochrome Haute Vitesse
Type ZWO ou QHY, capable de filmer à plus de 100 images/seconde pour figer le mouvement ultra-rapide.
Monture Équatoriale
Motorisée pour compenser la rotation de la Terre et garder le Soleil parfaitement centré.
⚫ Pourquoi du Monochrome ?
En astrophotographie solaire, on utilise souvent des caméras monochromes (noir et blanc). Comme on ne capture qu'une seule longueur d'onde (le rouge du H-alpha), un capteur couleur perdrait en résolution (car seuls les pixels rouges capteraient la lumière). L'image est ensuite colorisée ("fausses couleurs") au traitement pour lui donner cet aspect orange flamboyant qui correspond à notre imaginaire du Soleil.
Photographier le Soleil nécessite un équipement spécialisé pour éviter des dommages irréversibles aux yeux et au matériel. Pour réaliser cette image sans brûler son capteur, McCarthy utilise des filtres à bande étroite, spécifiquement des filtres H-alpha.
La Chromosphère et la raie H-alpha
La lumière visible du Soleil est dominée par la photosphère (la surface brillante). Cependant, pour voir les détails fascinants comme les protubérances et la texture de la surface, les astrophotographes isolent la raie spectrale de l'hydrogène alpha (H\(\alpha\)) à 656,28 nanomètres.
Ces filtres ne laissent passer qu'une bande passante ultra-fine (souvent inférieure à 1 Angström), bloquant 99,9% de la lumière intense. Cela révèle la chromosphère, l'atmosphère basse du Soleil située juste au-dessus de la photosphère. C'est grâce à cette technique que l'on distingue les textures granulaires et les filaments de plasma en arrière-plan du parachutiste, donnant à l'image son aspect dramatique et texturé.